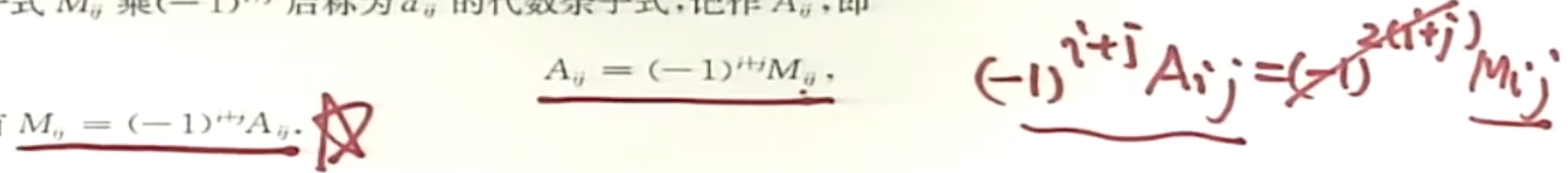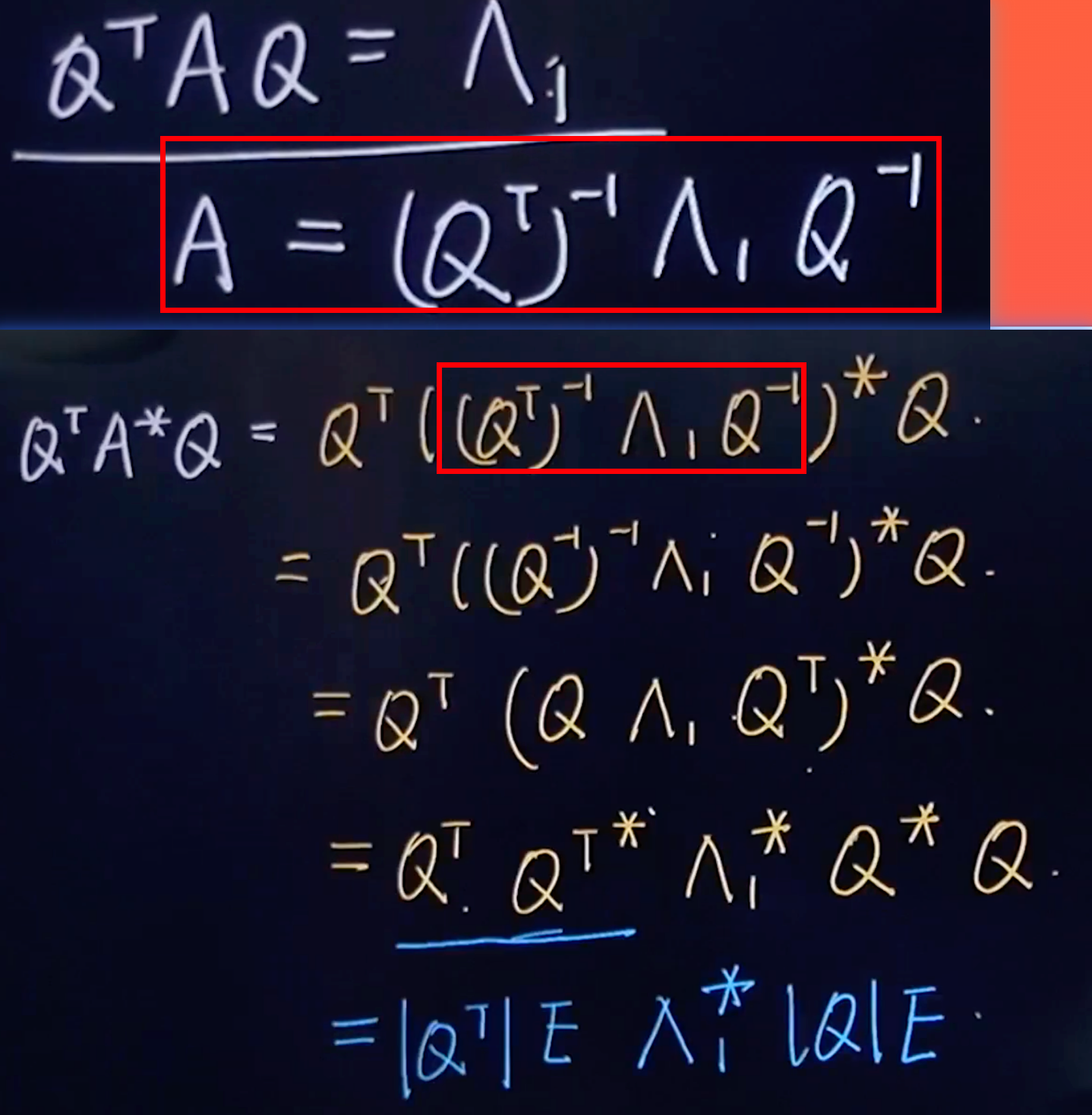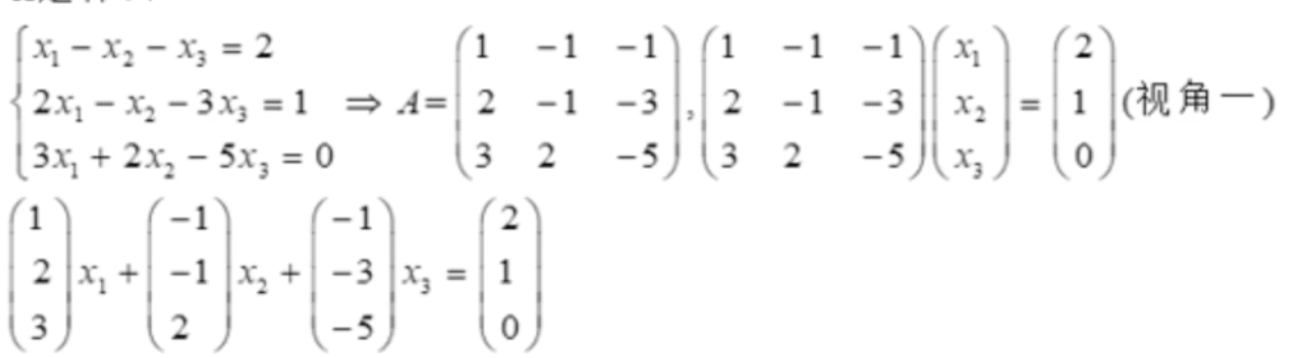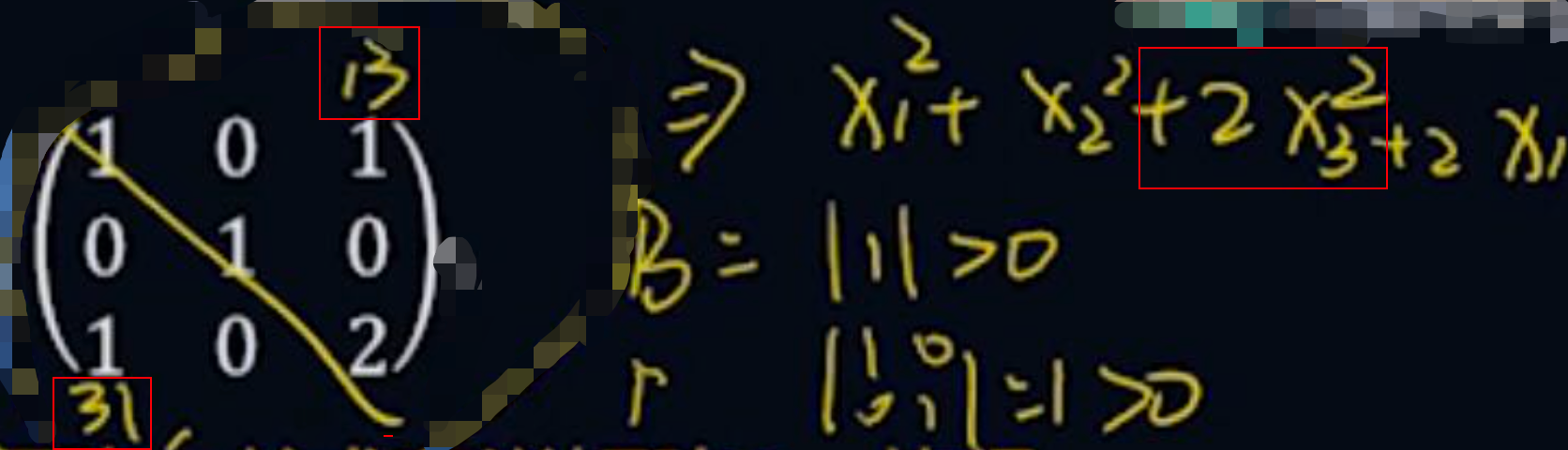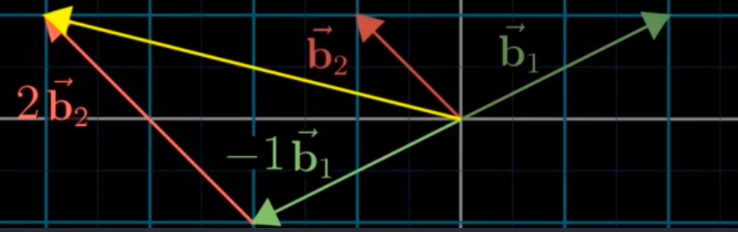
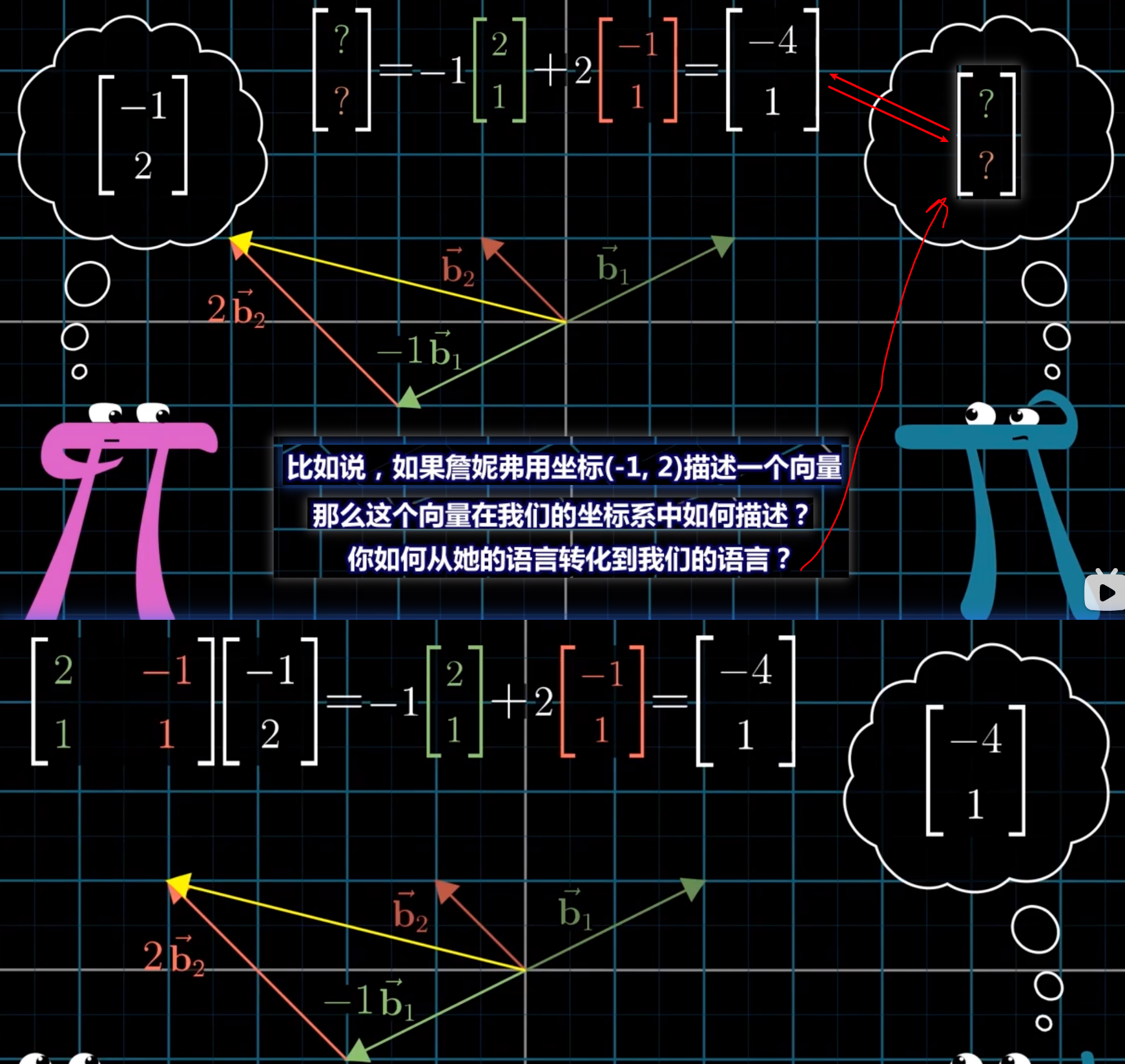
jenif的基向量<b1,b2>:
[10][01]
从我们的基向量看jenif的基向量:<b1,b2>
[21][−11]
转换矩阵T:
[21−11]
当jenif说她的向量 [−12]; 其实是指我们的向量 [−41]

[把未知数向下压缩为一点。(去重)] -> 组合转置放最右边
方程组 ---- ---- ----> 矩阵形式
|
| [把未知数向下压缩为一点。(去重)]
|
\/
向量组形式
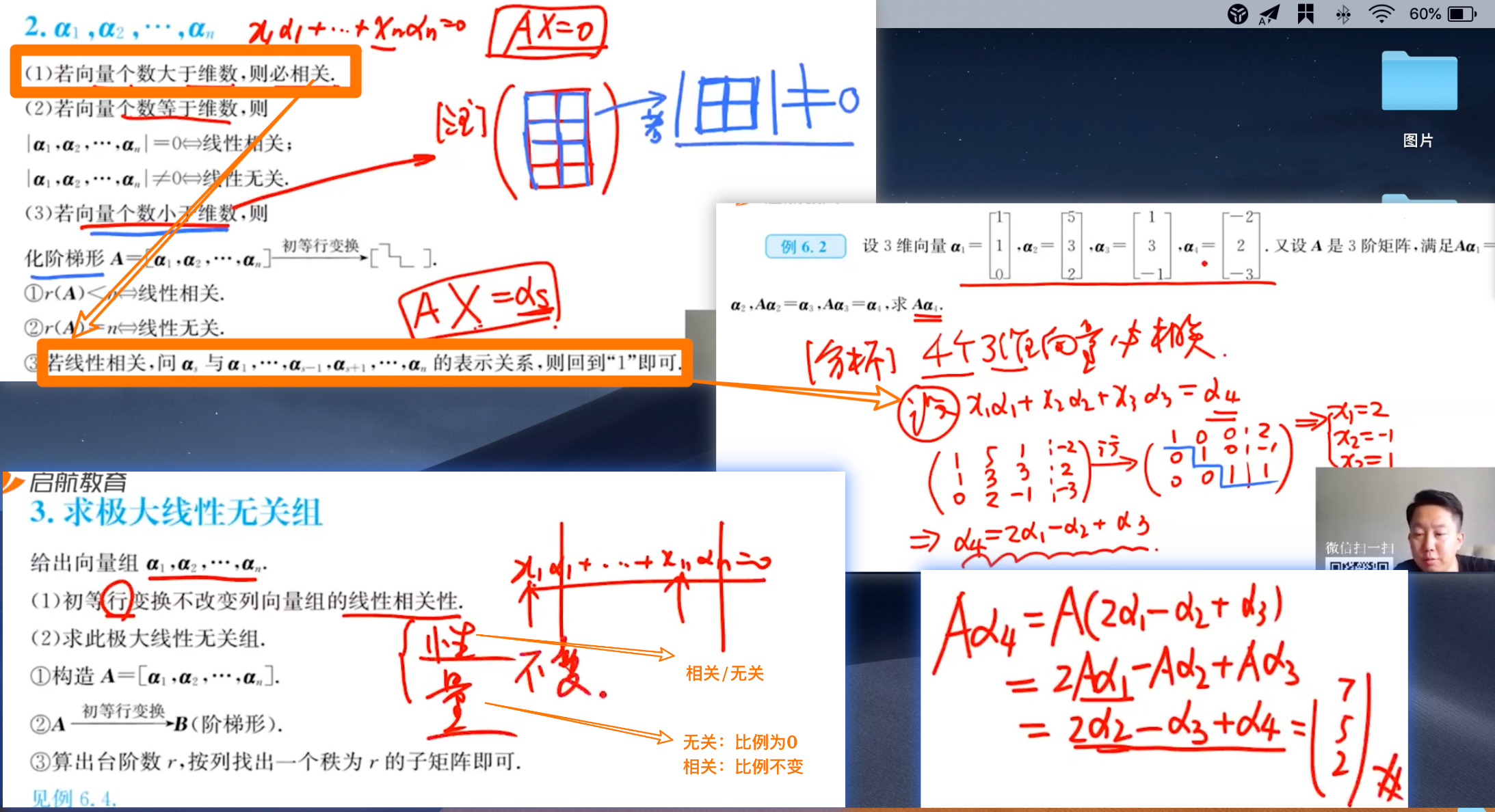
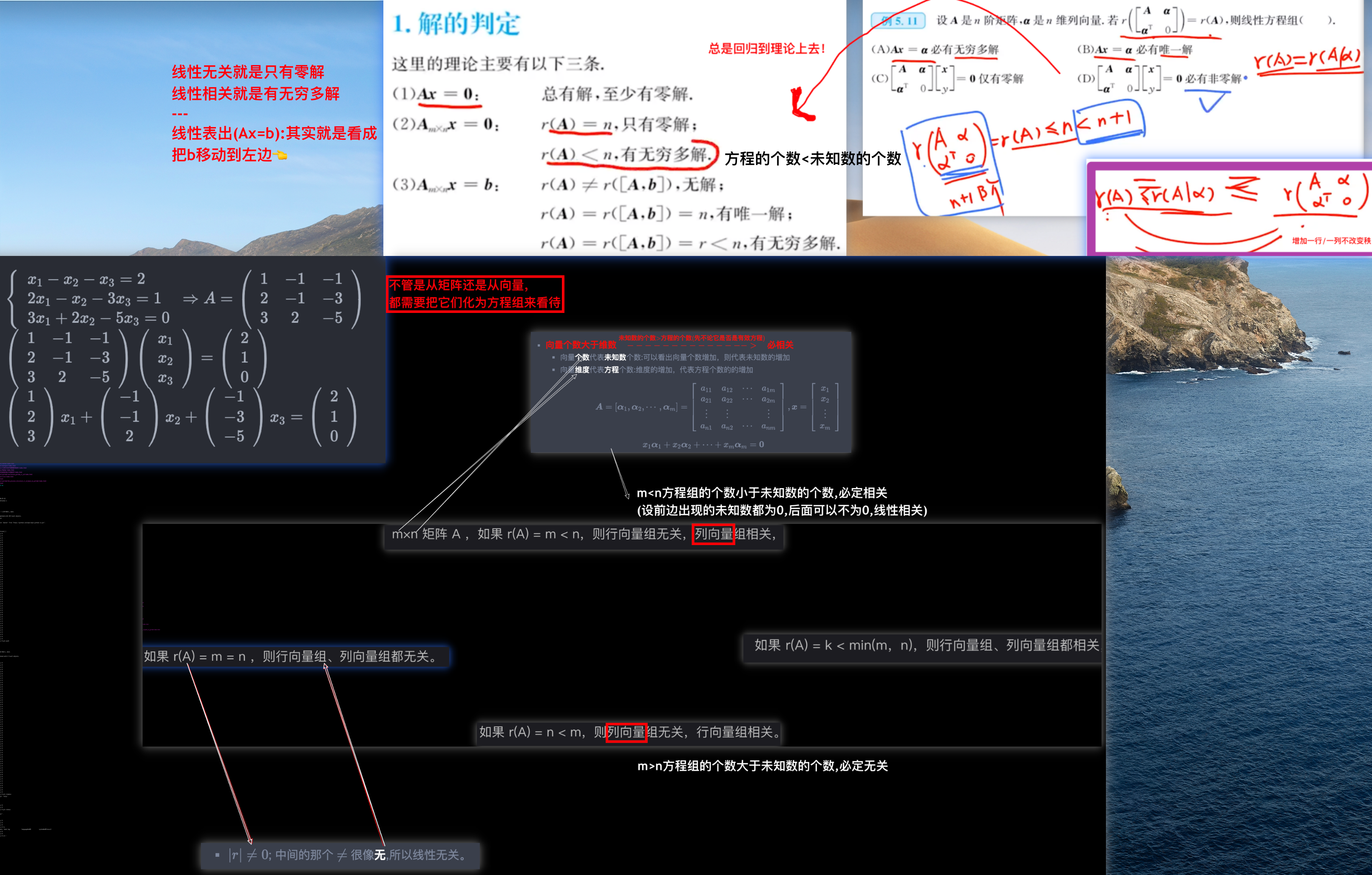
Am⋅nX=0 n为未知量的个数, r(A)与n去比较
Am⋅nX=b n为未知量的个数, r(A|b)与n去比较
去比较而不是说看列向量

-
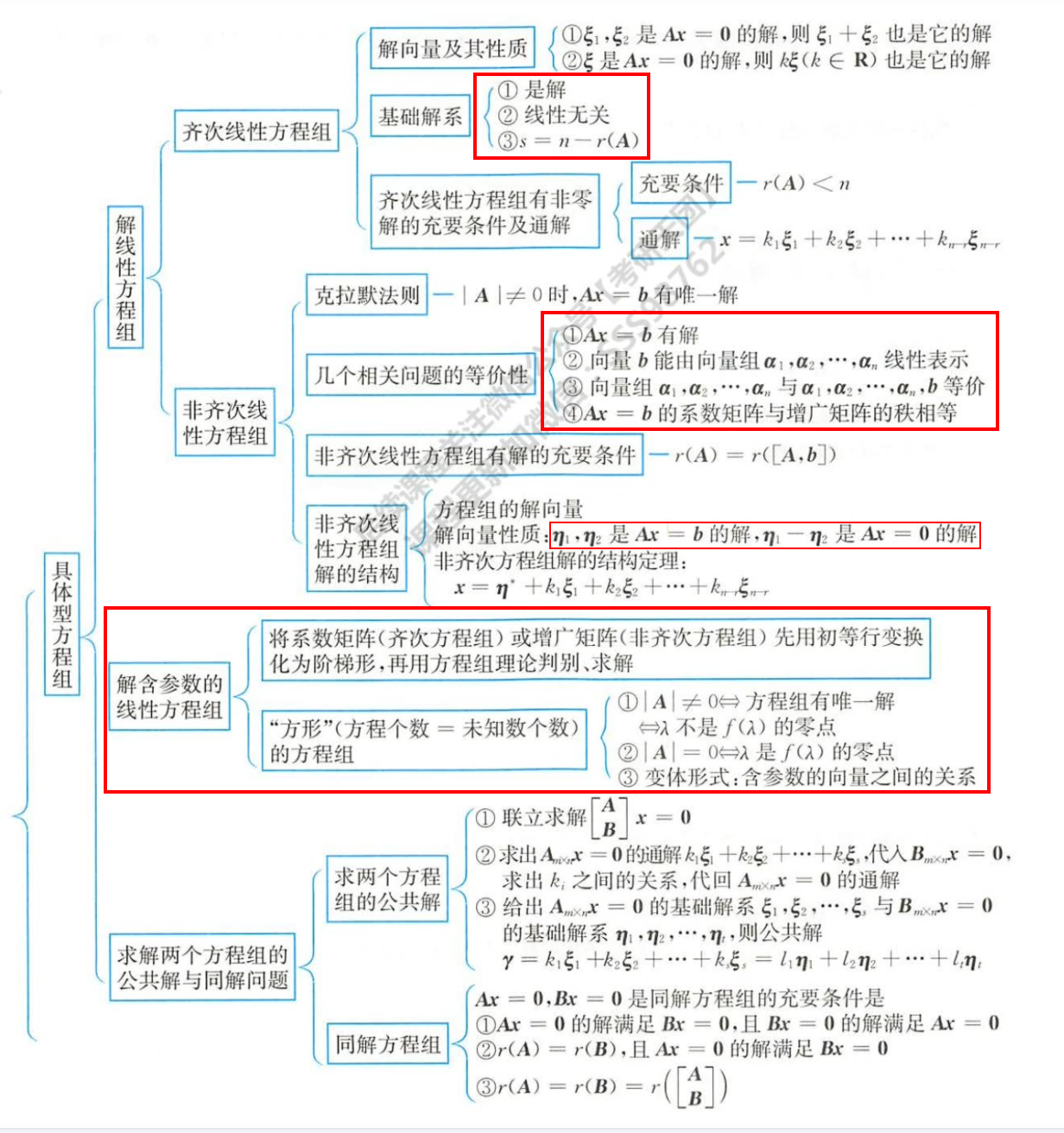
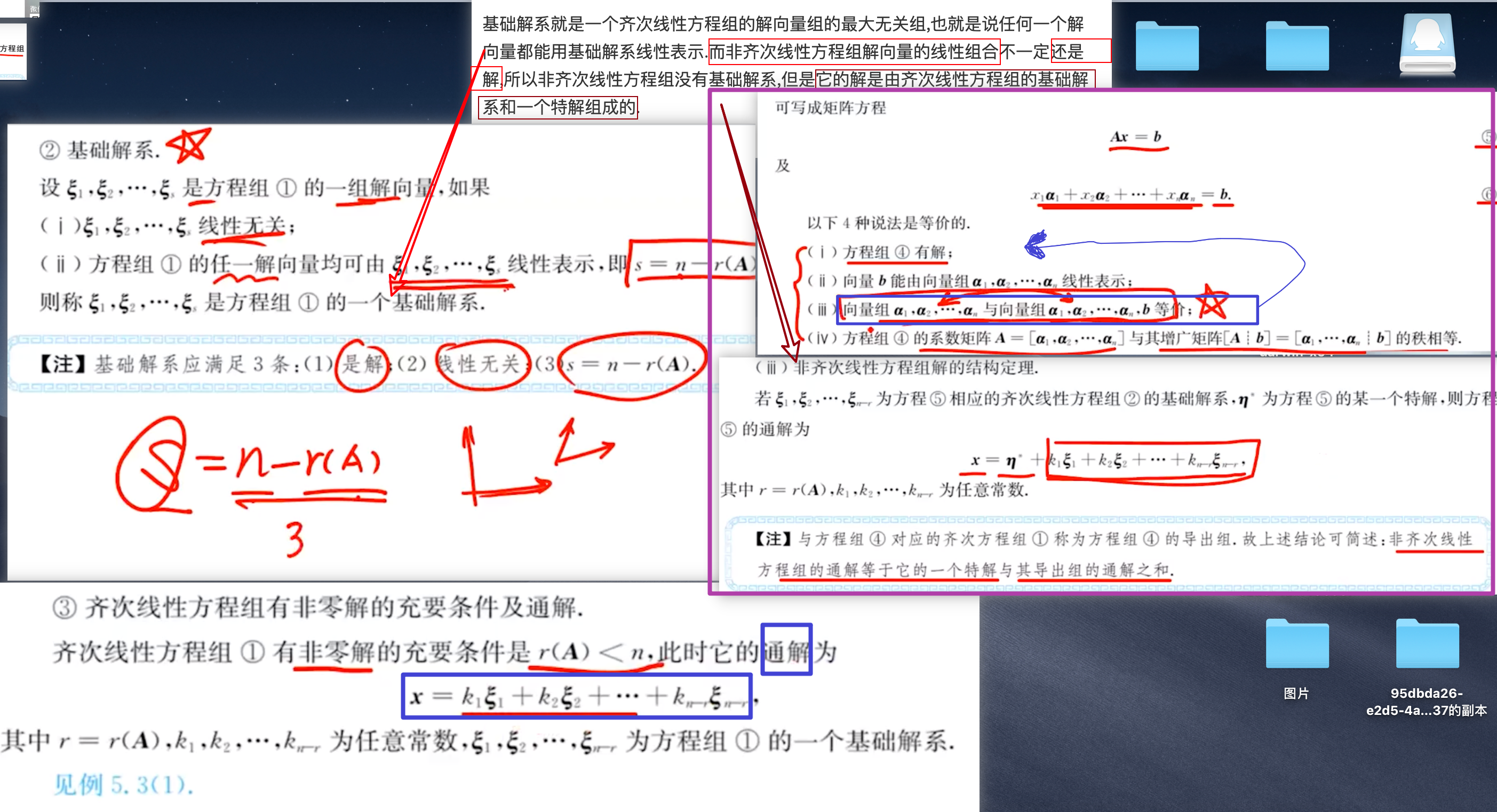
求基础解系步骤:
- s=n-r(A)
- 线性无关
- 是解: 齐次方程组解的线性组合,必然还是方程组的解。
-
克拉默法则
-
公共解/通解
-
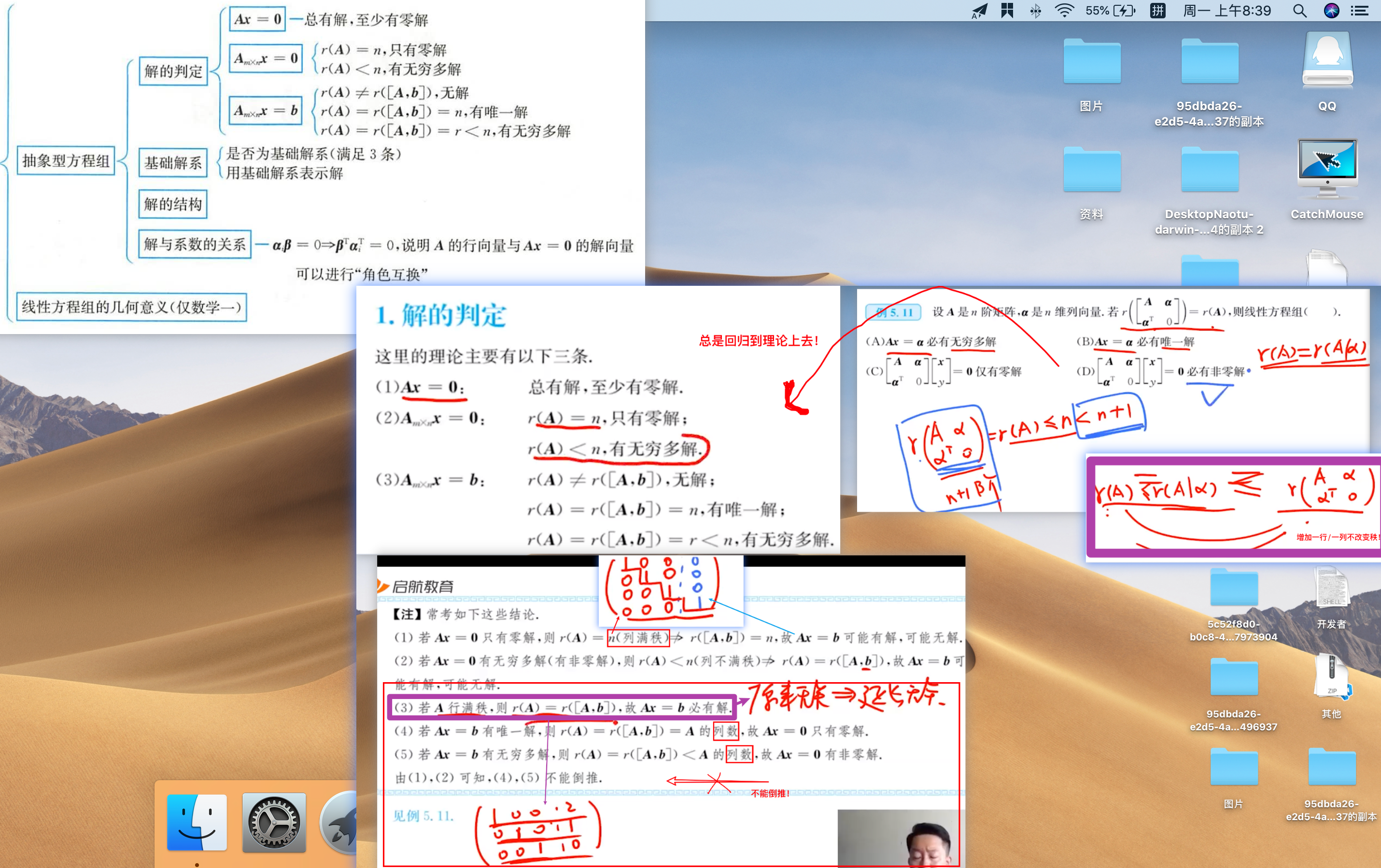
- 解的判定: r(A)与什么比较呢?如果是方阵那么很好取,如果是行列不等,那么应该取哪一个呢?
- 等于A列秩,因为 Am,n∗Xn,j;且如果是方程,那么j一定是1;未知数的个数就是A的列,方程个数就是A的行。


- 架好自由变量后,怎么求剩下值 [_,_,_,1,0,0]T 的呢?一定是从下到上来一步一步算出剩下的空的值
|
齐次方程 |
非齐次方程 |
| 有解 |
只有零解 |
有唯一解 |
| 有解 |
除零解外有无数个非零解 |
有无穷多解 |
| 无解 |
不可能无解(至少存在一个零解) |
无解 |
-
齐次方程组的解:
- 当r=n时,原方程组仅有零解;
- 当r<n时,有无穷多个解(从而有非零解)。
-
非齐次方程组的解:
轮回:判断解类型:比较秩与未知数的个数:秩->矩阵->矩阵的运算->分块矩阵->
\_>求秩->行阶梯,行最简,初等变换,非零子式->行列式->求方程组解的类型。
xxxxxxxxxxxxxxx
xx x
xx x
xx x
xxx x x
xx x x x
x x x x
x x x x
xx x x x
x x x
x x x x
x xx x x
x xx x x
xx x
xxx x
xxxxxxxxxxxx
m*n的矩阵 (m行*n列)
看作方程组,方程的个数m, 未知数的个数n
3行3列
看作方程组,方程的个数3, 未知数的个数3
⎣⎡123−1−12−1−3−5⎦⎤
3行4列
看作方程组,方程的个数3, 未知数的个数4
⎣⎡123−1−12−1−3−5210⎦⎤
- 代数加减乘: An
-

- 从内部性质来看
- An=(X)n−1A ; 其中X可为迹(主对角相乘)/K
- 从内部瓦解
- 借助外力(初等矩阵/相似)
-
代数除: A−1
-
代数方程:矩阵方程
- r(A) ⟶?秩与方程未知数的个数大小关系 n(方程未知数的个数,不是方程的个数)
⎩⎨⎧x1−x2−x3=22x1−x2−3x3=13x1+2x2−5x3=0⇒A=⎝⎛123−1−12−1−3−5⎠⎞⎝⎛123−1−12−1−3−5⎠⎞⎝⎛x1x2x3⎠⎞=⎝⎛210⎠⎞⎝⎛123⎠⎞x1+⎝⎛−1−12⎠⎞x2+⎝⎛−1−3−5⎠⎞x3=⎝⎛210⎠⎞
分为上/中/下式子;
从上->中引出矩阵的概念。====>如何运算?引出矩阵的乘法(左行右列)
从中->下引出了分块的概念。===>分块矩阵。

- 概念性质的结论一定要从定义(矩阵/向量)入手去理解:
- 向量:什么是向量组的秩?
- 从定义上的描述,秩是向量组的最大线性无关组所包含的向量个数,但更为直观的理解是:秩是描述一个向量组“表出能力”的数字,它表示向量组能够表出的线性空间的维度是多少,但并不记录它能表出哪些维度。
- B能被A表出,则r(B)≤r(A),这其实很好理解:
- ①向量组能表示出的线性空间维度取决于构成它的向量本身(就跟不能用二维坐标直接去表示任意的三维空间坐标一样)
- ②对于已经定义好向量表示形式的向量组而言,它自身也不可能表出具有别的维度的向量组(比如[1,0,0]和[0,1,0]无论如何也不可能表出[0,0,1]这个向量)。因此表出结果的秩只可能变小或者维持相等(这也是有r(AB)≤r(A),r(B)的原因,因为矩阵乘法本身就是对向量组的一种线性变化)。
- 就像我(A)兜里有橘子、苹果和香蕉,而你(B)兜里的水果全都来自与我(表出关系),那你兜里的水果种类一定只能比我少或相等;
- 要使得A和B秩相同, 条件需要补充成A和B能互相线性表出,这种关系我们称为向量组A和B等价。
- 需要注意“A和B能互相线性表出”是“A和B秩相同”的充分条件而不是必要条件,因为在A和B并不是满秩的情况下,他们可能刚好都能表示n(n<N)维空间,但并非表示的相同的n维,这时候二者等秩但并不能相互线性表出(注意开始提到的秩的概念)。
- 这也很好理解:我(A)手里有橘子和苹果,你(B)手里有橘子和香蕉,我俩水果种类都是2,但是我们不存在表出关系。
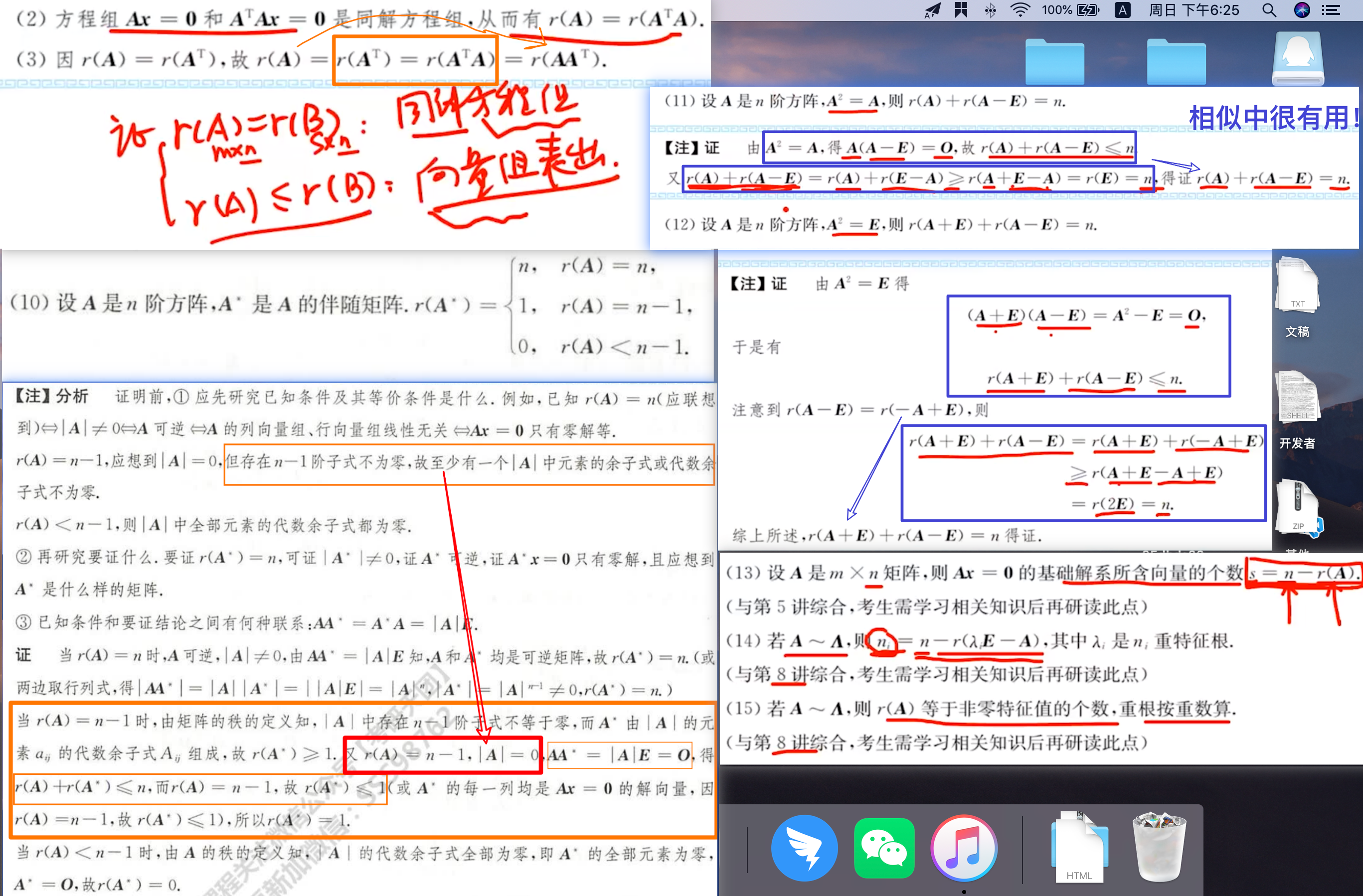
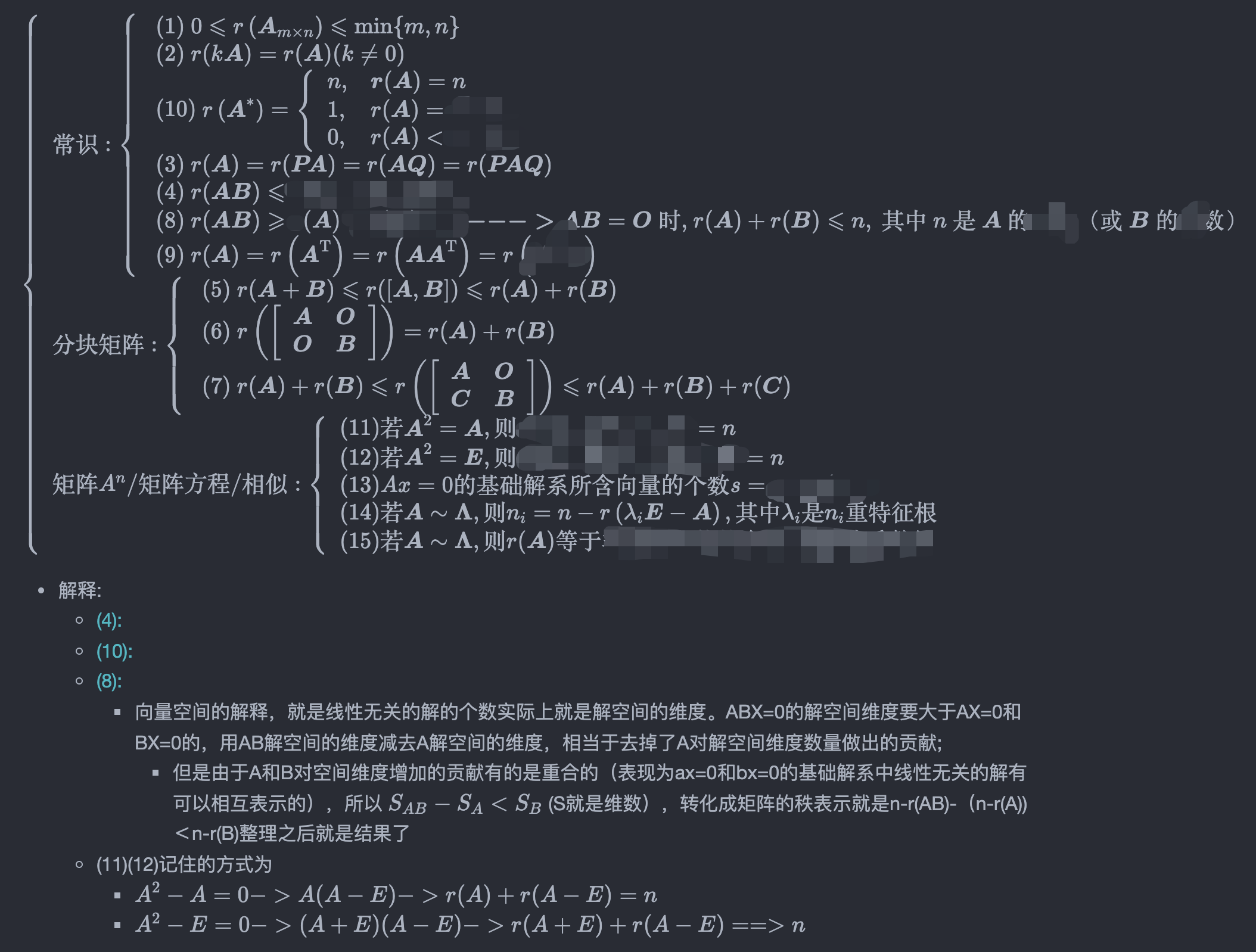
⎩⎨⎧常识:⎩⎨⎧ (1) 0⩽r(Am×n)⩽min{m,n} (2) r(kA)=r(A)(k=0) (10) r(A∗)=⎩⎨⎧n,1,0,r(A)=nr(A)=n−1r(A)<n−1 (3) r(A)=r(PA)=r(AQ)=r(PAQ);设A是m×n矩阵,P,Q分别是m阶、n阶可逆矩阵 (4) r(AB)⩽min{r(A),r(B)} (8) r(AB)⩾r(A)+r(B)−n−−−>AB=O 时, r(A)+r(B)⩽n, 其中 n 是 A 的列数(或 B 的行数) (9) r(A)=r(AT)=r(AAT)=r(ATA)分块矩阵:⎩⎨⎧ (5) r(A+B)⩽r([A,B])⩽r(A)+r(B) (6) r([AOOB])=r(A)+r(B) (7) r(A)+r(B)⩽r([ACOB])⩽r(A)+r(B)+r(C)矩阵An/矩阵方程/相似:⎩⎨⎧(11)若A2=A,则r(A)+r(A−E)=n(12)若A2=E,则r(A+E)+r(A−E)=n(13)Ax=0的基础解系所含向量的个数s=n−r(A)(14)若A∼Λ,则ni=n−r(λiE−A),其中λi是ni重特征根(15)若A∼Λ,则r(A)等于非零特征值的个数,重根按重数算
- 解释:
- (3):初等变换不影响矩阵的秩
- 初等变换法:对(AE)⟶作初等变换(EA−1)
- (4):
- (10): 已知伴随的秩可以反推矩阵的秩
- (8):
- 向量空间的解释,就是线性无关的解的个数实际上就是解空间的维度。ABX=0的解空间维度要大于AX=0和BX=0的,用AB解空间的维度减去A解空间的维度,相当于去掉了A对解空间维度数量做出的贡献;
- 但是由于A和B对空间维度增加的贡献有的是重合的(表现为ax=0和bx=0的基础解系中线性无关的解有可以相互表示的),所以 SAB−SA<SB (S就是维数),转化成矩阵的秩表示就是n-r(AB)-(n-r(A))<n-r(B)整理之后就是结果了
- (11)(12)记住的方式为
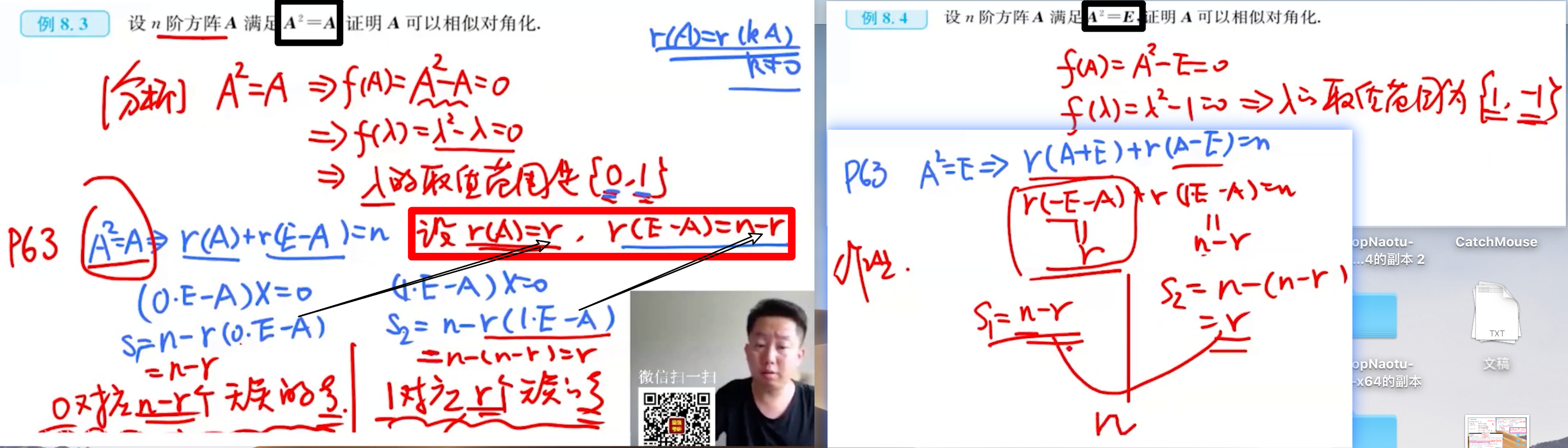
- A2−A=0−>A(A−E)−>r(A)+r(A−E)=n
- A2−E=0−>(A+E)(A−E)−>r(A+E)+r(A−E)==>n
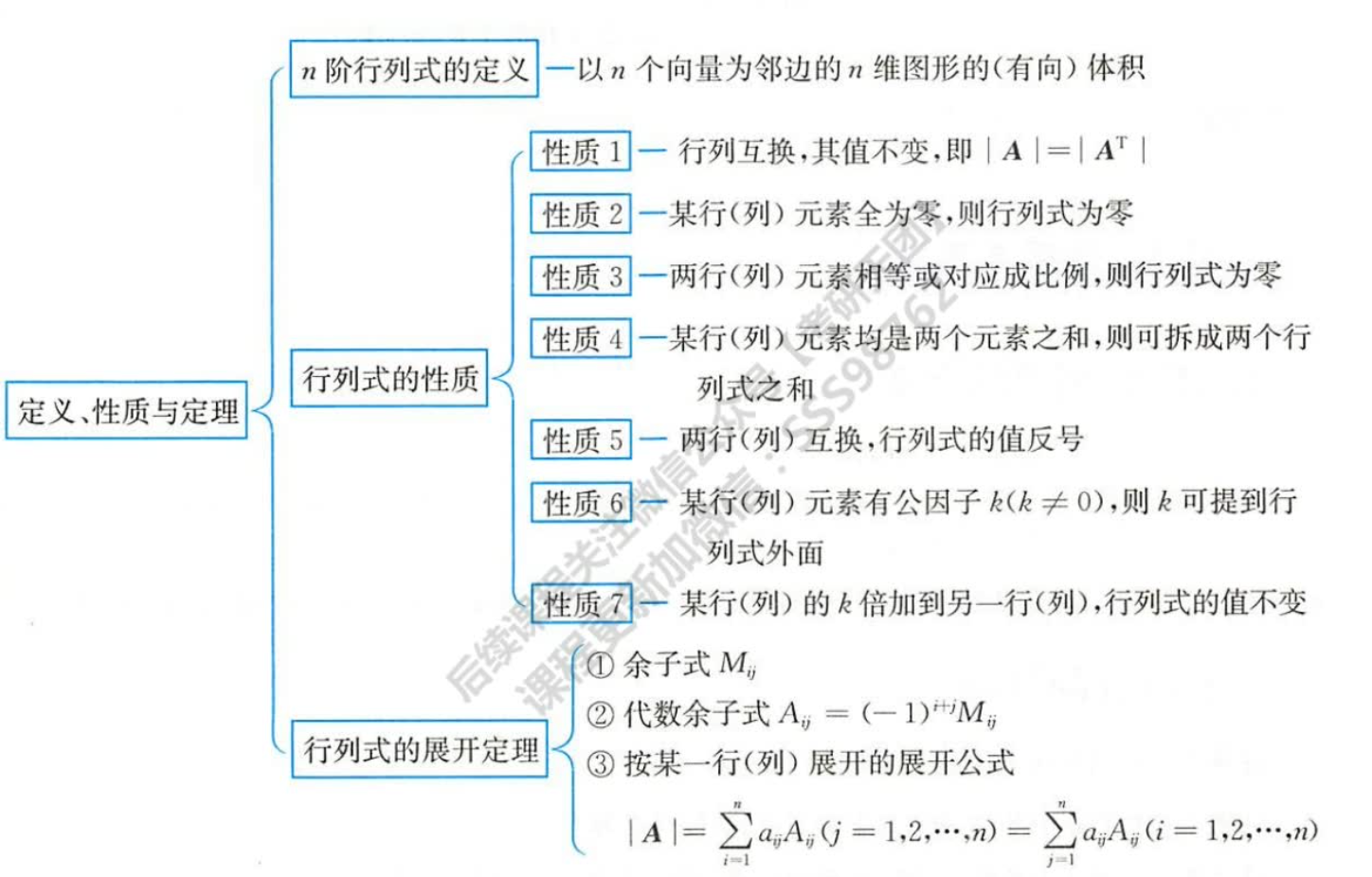
什么是非零子式? ===>跟行列式有关 行列式的概念
-
define:
- 不能单独的把它看作数字,要看作向量,然后多个向量组成的向量组。
- 一维:相当于一个数字;
- 二维:相当于面积;
- 三维:相当于体积,行列式就是向量组的体积.
- D3=0 => V=0 => α,β,γ 线性相关
- D3=0 => V = 0 => α,β,γ 线性无关(因为不在一个平面上,肯定线性无关)
- 所以当他为零的几种情况:
- 一维向量等于0,二维共线,三维共面
- 至少有两个向量平行
- 余子式: Mij
-
nature:
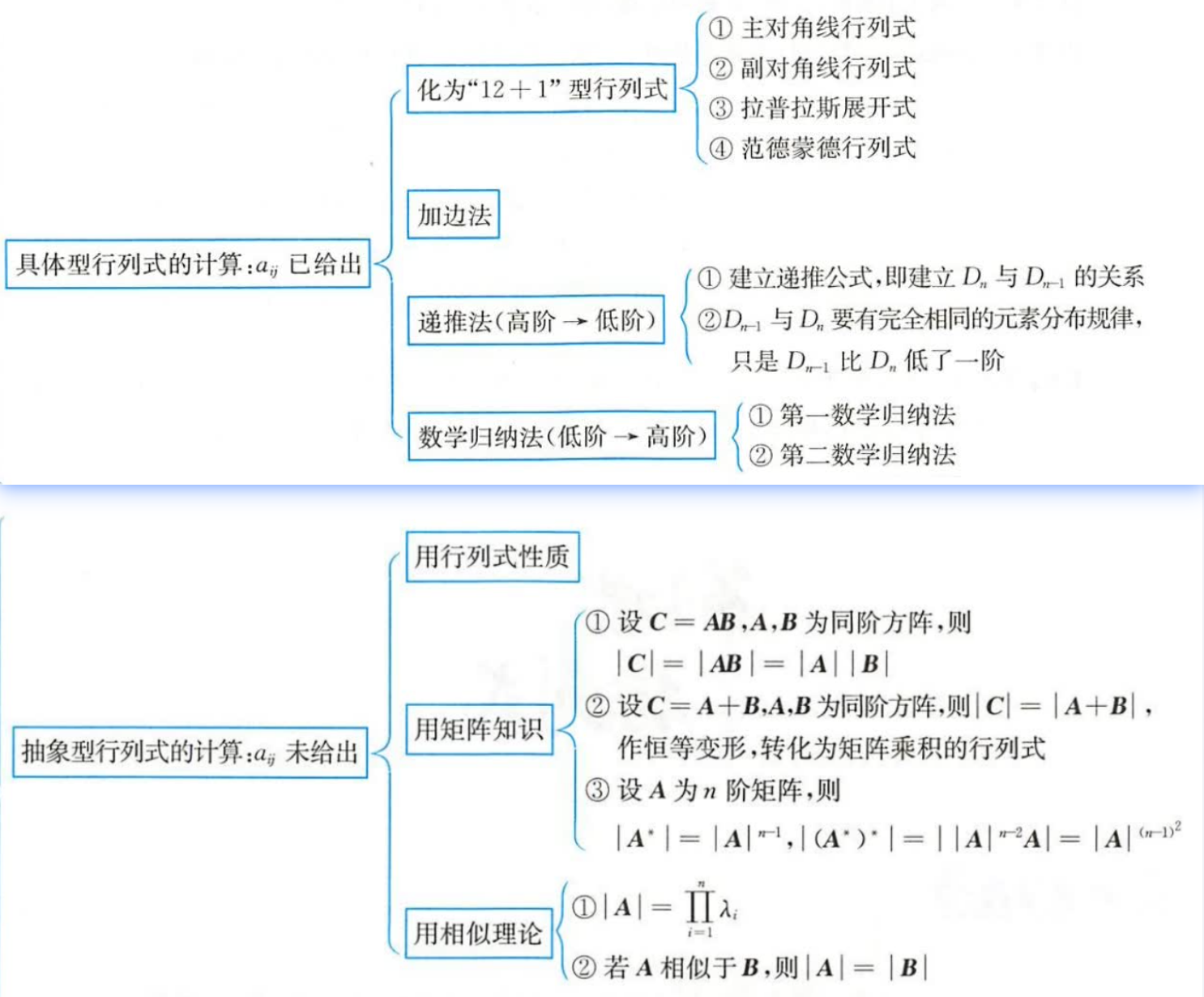
- 行列式的计算。
- 具体:
- 抽象:
- 用行列式的性质
- 用矩阵知识
- ∣C∣=∣AB∣=∣A∣∣B∣
- ∣C∣=∣A+B∣=恒等变形,化为上式的两矩阵相乘∣a(b1+b2)∣=∣a∣∣b1+b2∣
- ∣A∗∣=∣A∣n−1,∣(A∗)∗∣=∣∣A∣n−2A∣=∣A∣(n−1)2
- A⋅A∗=∣A∣⋅E→∣A∣⋅∣A∗∣=∣A∣n
- ∣kA∣=kn∣A∣⎩⎨⎧(kA)⊤=kA⊤(kA)∗=kn−1A∗(kA)−1=k1A−1
- 相似理论:
TODO
- 任何方阵都有伴随矩阵,
- |A|=0;仍有伴随矩阵,只是不能用A∗=(∣A∣1A)−1=∣A∣A−1,只能使用代数余子式求(用定义)

⎝⎛123⎠⎞x1+⎝⎛−1−12⎠⎞x2+⎝⎛−1−3−5⎠⎞x3=⎝⎛210⎠⎞
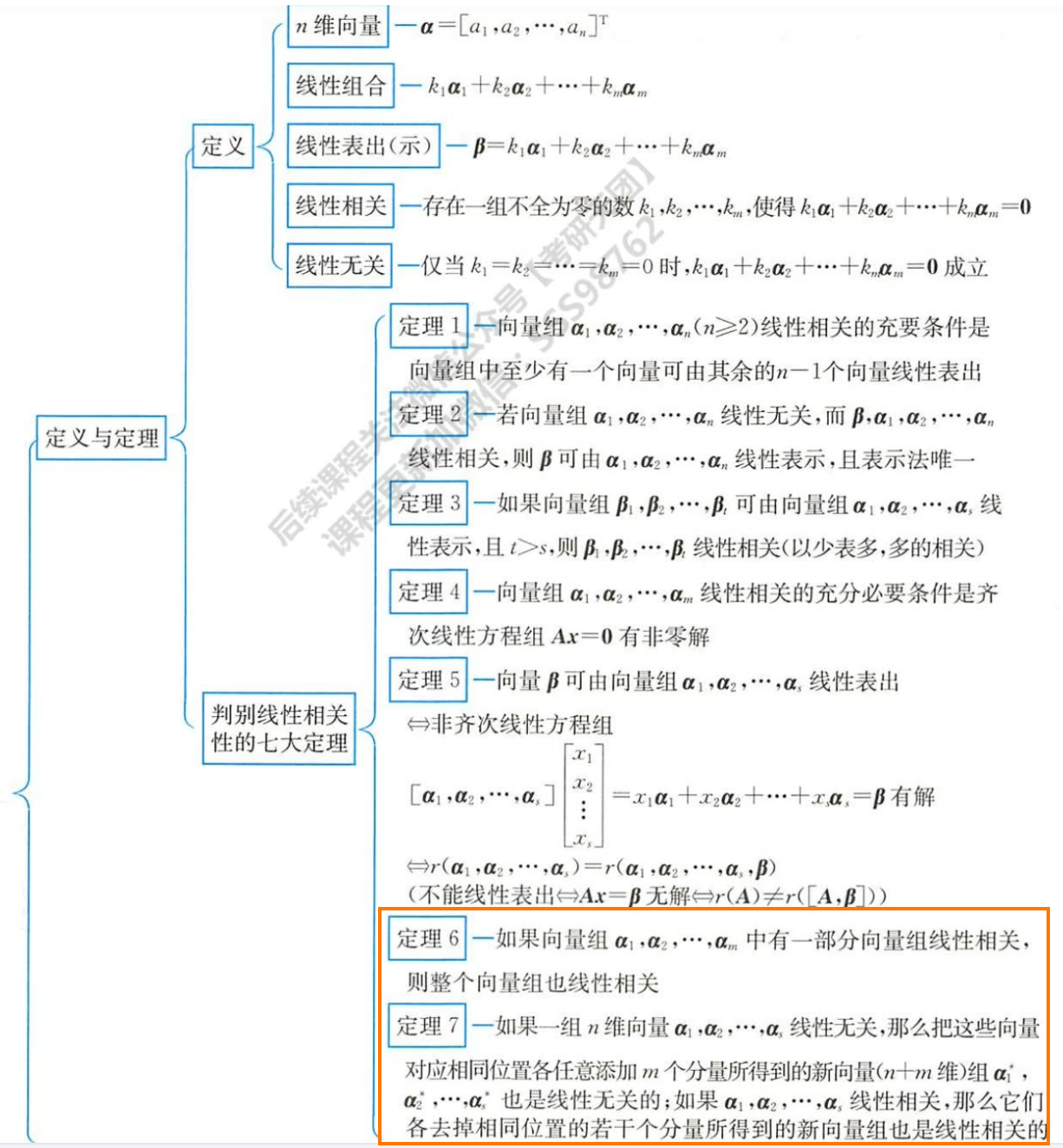
-
定理7:列无关,延长行(增加维度),还是无关
- r(A)m⋅n=m;r(A∣b)m⋅(n+1), 行满秩,再加一列,不影响行的秩
-
线性表示 / 线性相关-无关
- 向量之间的关系(相关-无关/表示)要从两个方面来分析:
-
从向量之间的关系来:
- 成比例的向量,为0的向量 ==> 线性相关
- 单个非零向量,两个不成比例的向量 ==> 线性无关
-
从方程组的角度来分析
- 线性表示/不能线性表示 ====>类比AX=B 非齐次方程组
- 线性表示(出) ====>类比AX=B 非齐次方程组的有解(唯一解也好/无穷解也好,只要有解)
- 线性表示 ====>多个向量进行线性表示 向量等价
- 线性无关/线性相关 ====>类比AX=0 齐次方程组
- 线性无关 ====>类比AX=0 齐次方程组的有零解
- 线性相关 ====>类比AX=0 齐次方程组的有无穷多个解(从而有非零解)
- 能不能把线性相关无关这些概念 ====>极大线性无关组 跟r(A)联系起来 ( ====>有效方程个数 方程组)
| 向量 |
方程组 |
| 个数 |
未知数 |
| > 个数++-- |
未知数++-- |
| >> 部分线性相关,整体线性相关 |
click |
| >> 整体线性无关,部分线性无关 |
这个很好理解 |
| ----------------------------------------------- |
- |
| 维度 |
方程个数 |
| 维度++-- |
方程个数++--(约束条件的变化) |
| 线性相关-无关 |
齐次AX=0 |
| > 线性无关 |
齐次AX=0;只有零解 |
| >> 原来无关,延长必无关(原来就是无缘的人,延长时间还是无关) |
只有零解的情况下,减少约束条件,有零解/∞解;增加约束条件,只会有零解 |
| >> 原来相关,缩短必相关 (原来就是有缘的人,缩短时间还是能一见钟情) |
有∞解的情况下,减少约束条件,∞解;增加约束条件,只有零解/有∞解 |
| > 线性相关 |
齐次AX=0;有∞解 |
| 线性表示(出) |
非齐次AX=B |
-

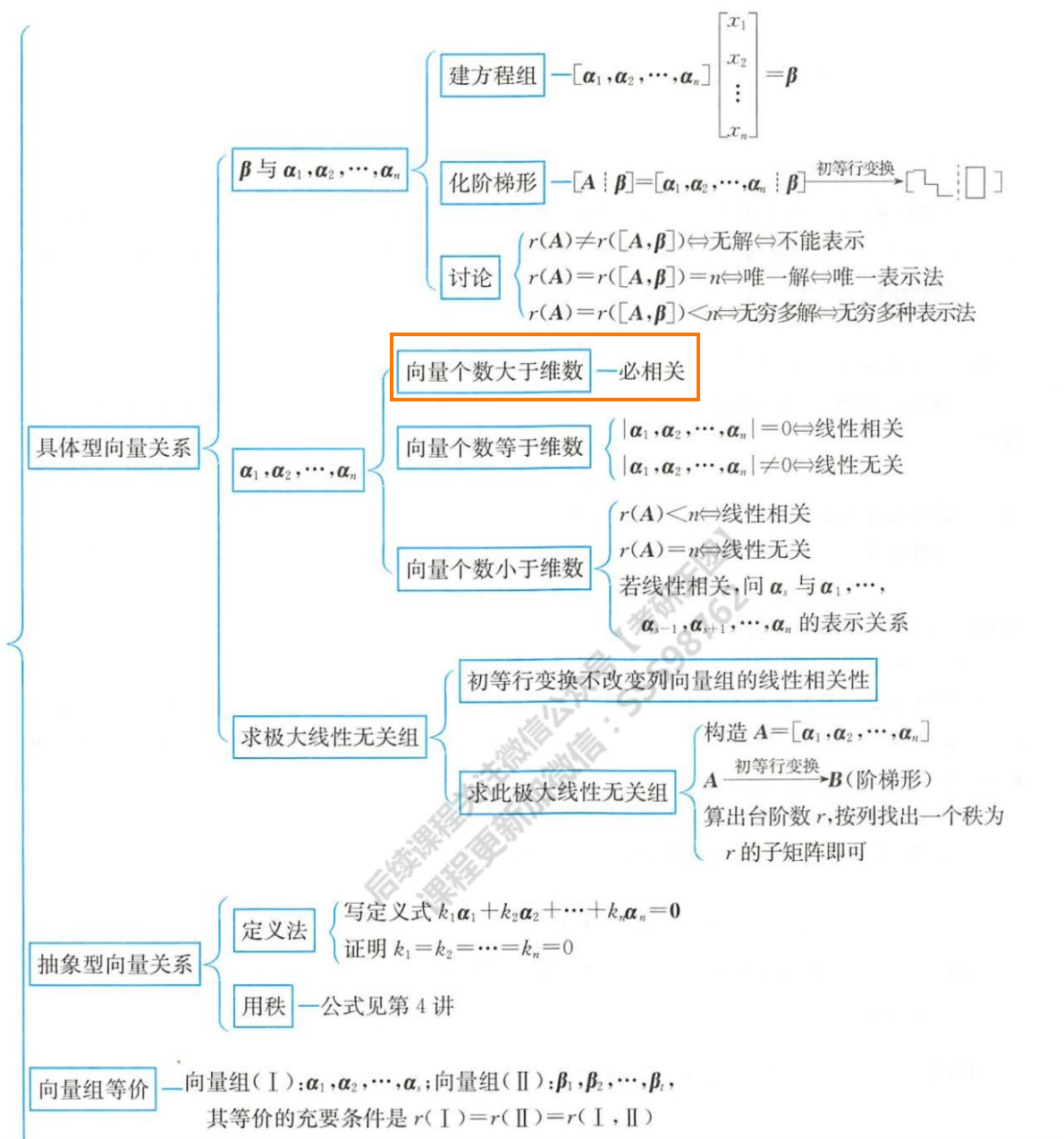
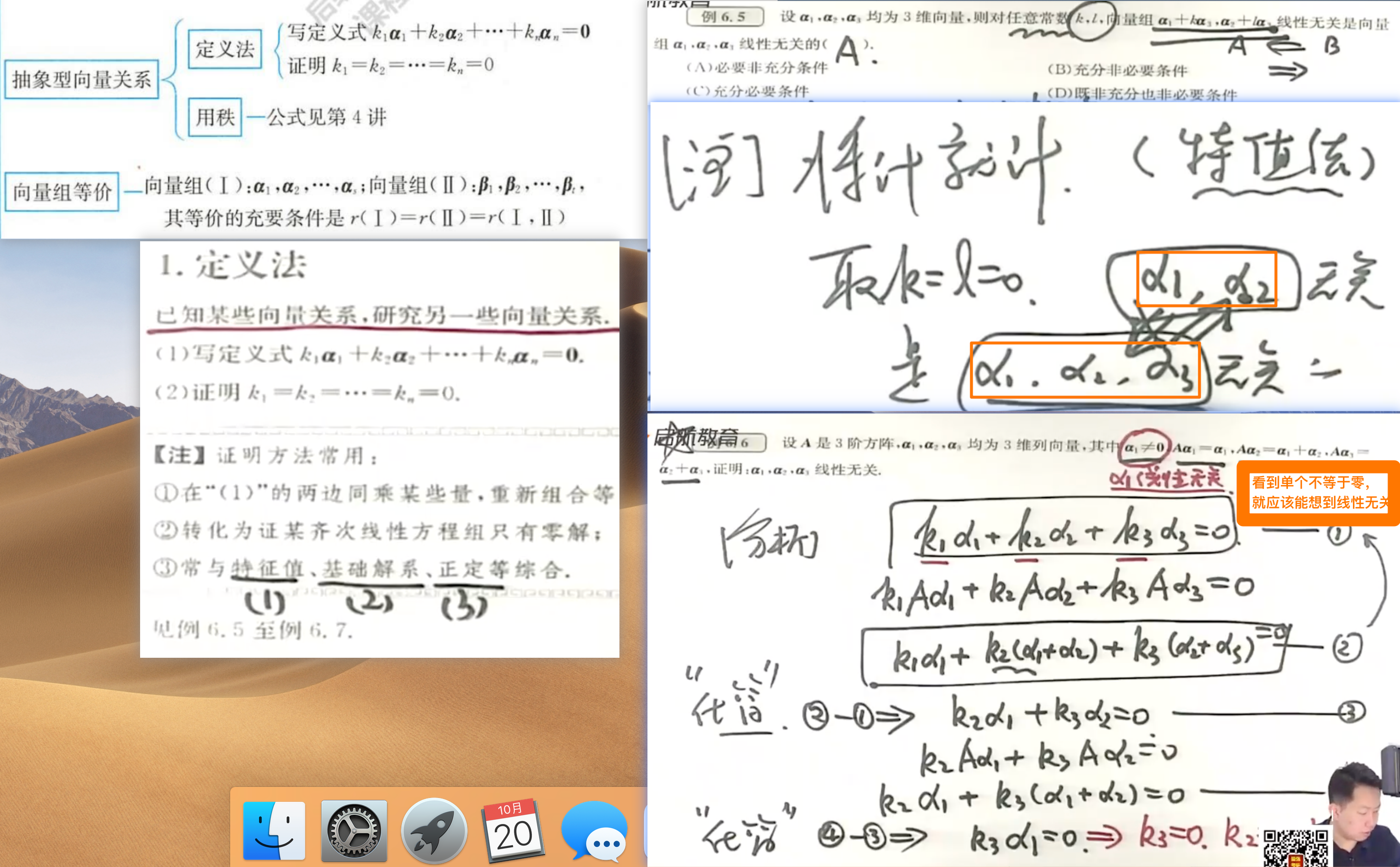
有解无解判定成功后,有解如何表示?
尤其是无穷多解。

怎么表示无穷多解? <========引出解个数判定,让它们自由组合(在前面赋予系数k1,k2...) 无穷多个解中选出几个具有代表性的解。
代表性的解 ========> 线性无关的解
行列式里面都是方的
相似理论-特征值/向量都是方的
二次型一定是方的
- 特征值-特征向量:
- ∣3A+2E∣=0⇒λ=−32→−ab


-
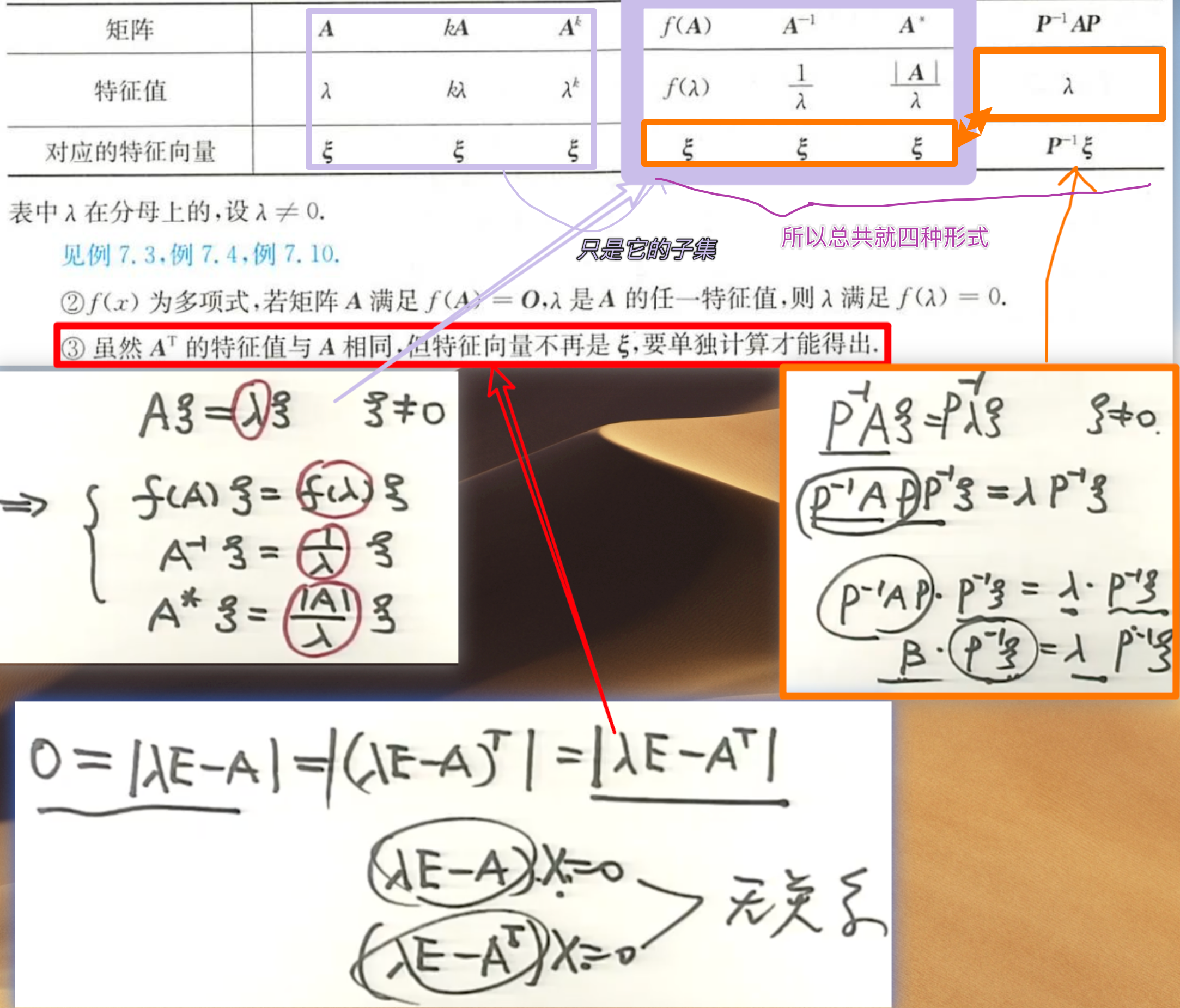
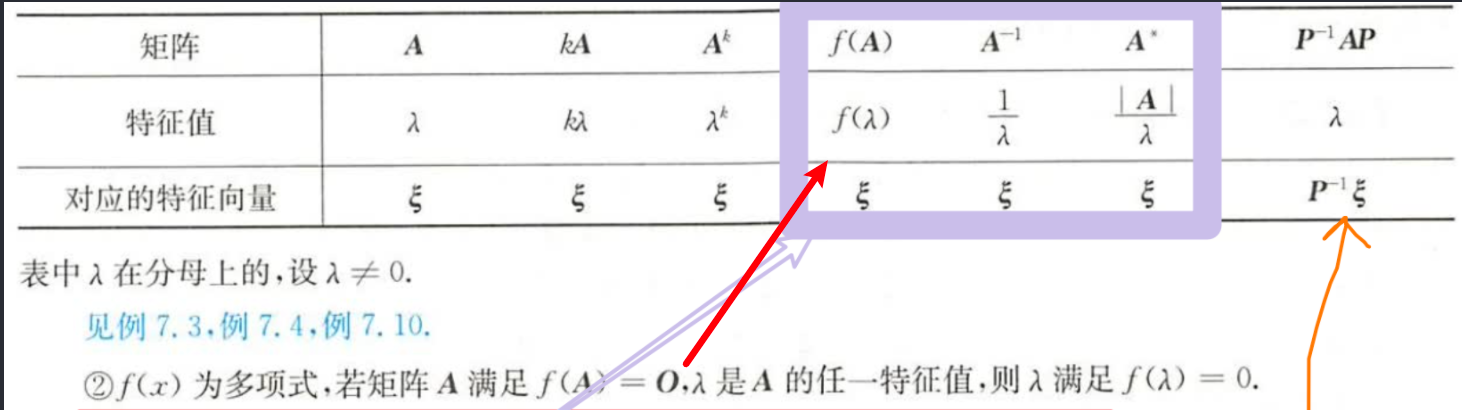
特征值命题:
- f(A)ξ=f(λ)ξ
- A−1ξ=λ1ξ
- A∗ξ=λ∣A∣ξ
- (P−1AP)(P−1ξ)=λ(P−1ξ)
-
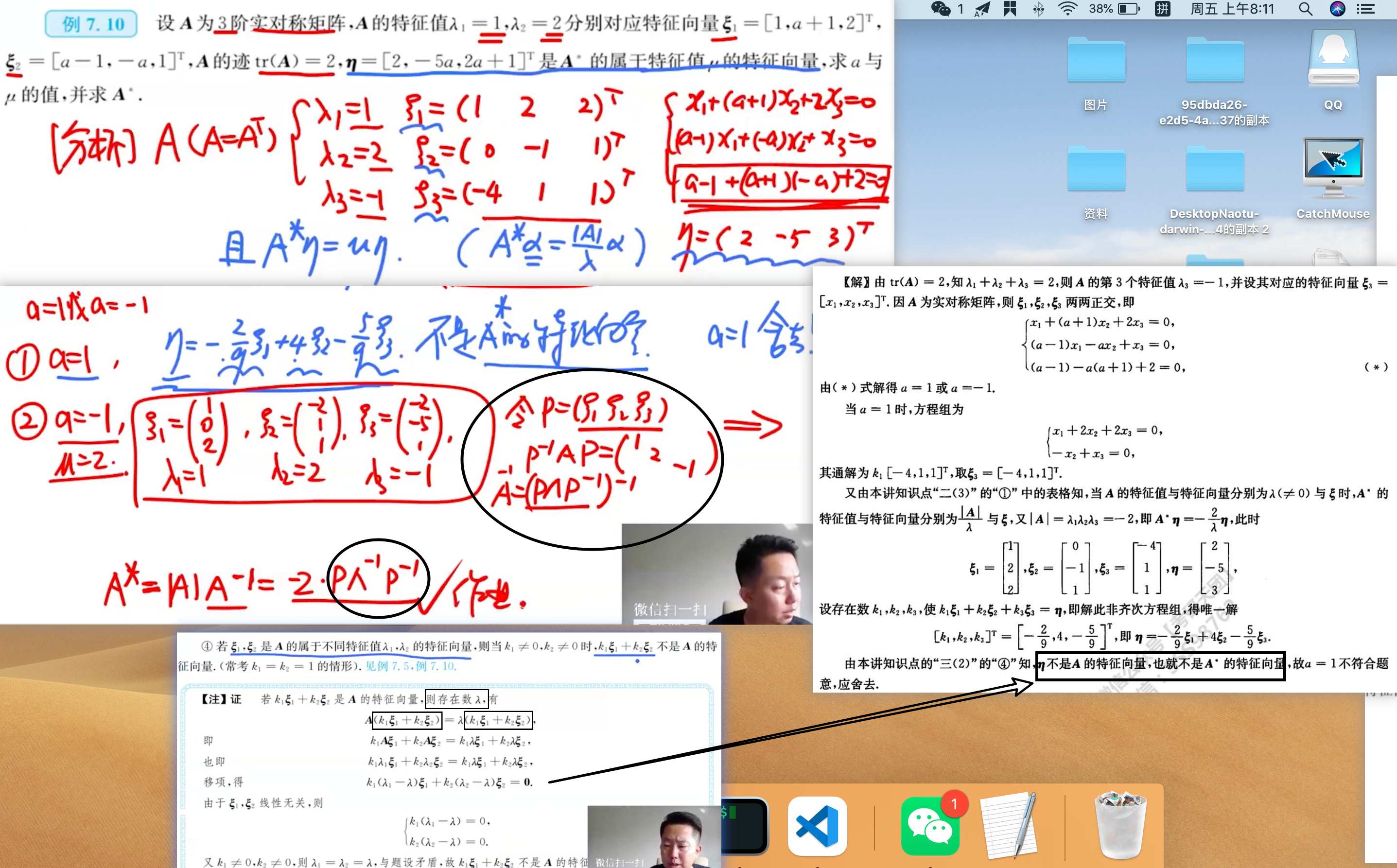
特征向量例子:
-

- 矩阵方程命题:

相似合同这里的判定:
- 相似合同
- 判断合同:
- 用定义法:A,B合同⇔存在可逆矩阵C,使得CTAC=B.
- 用正、负惯性指数: A,B合同⇔pA=pB,qA=qB.(相同的正、负惯性指数)
- 同阶实对称矩阵 A,B相似必合同;
- A=AT;B=BT,且A~B
- 下面这一条应该是错的,特征值相同,不能推出合同=>实对称矩阵A,B相似⟶因实对称矩阵→必定可以相似对角化有相同的特征值/特征向量⟶⟶⟶⟶⟶⟶⟶⟶pA=pB,qA=qB(相同的正负惯性指数⇔A,B合同)A,B必合同
- 为什么是对称矩阵必有可逆矩阵C,使得CTAC=Λ, 其中 Λ 为对角矩阵?
- 实对称矩阵有正交矩阵C, C−1AC=CTAC=Λ
- 所以实对称矩阵相似,就有相同的Λ,所以CTAC=C1TAC1−>A=(C1⋅C−1)TB(C1⋅C−1), 所以不是通过上面的用特征值相同得到正负惯性得到
- 用传递性: A合同于C,C合同于B,则A合同于B.
- 实对称矩阵/正交矩阵(四/二性质)
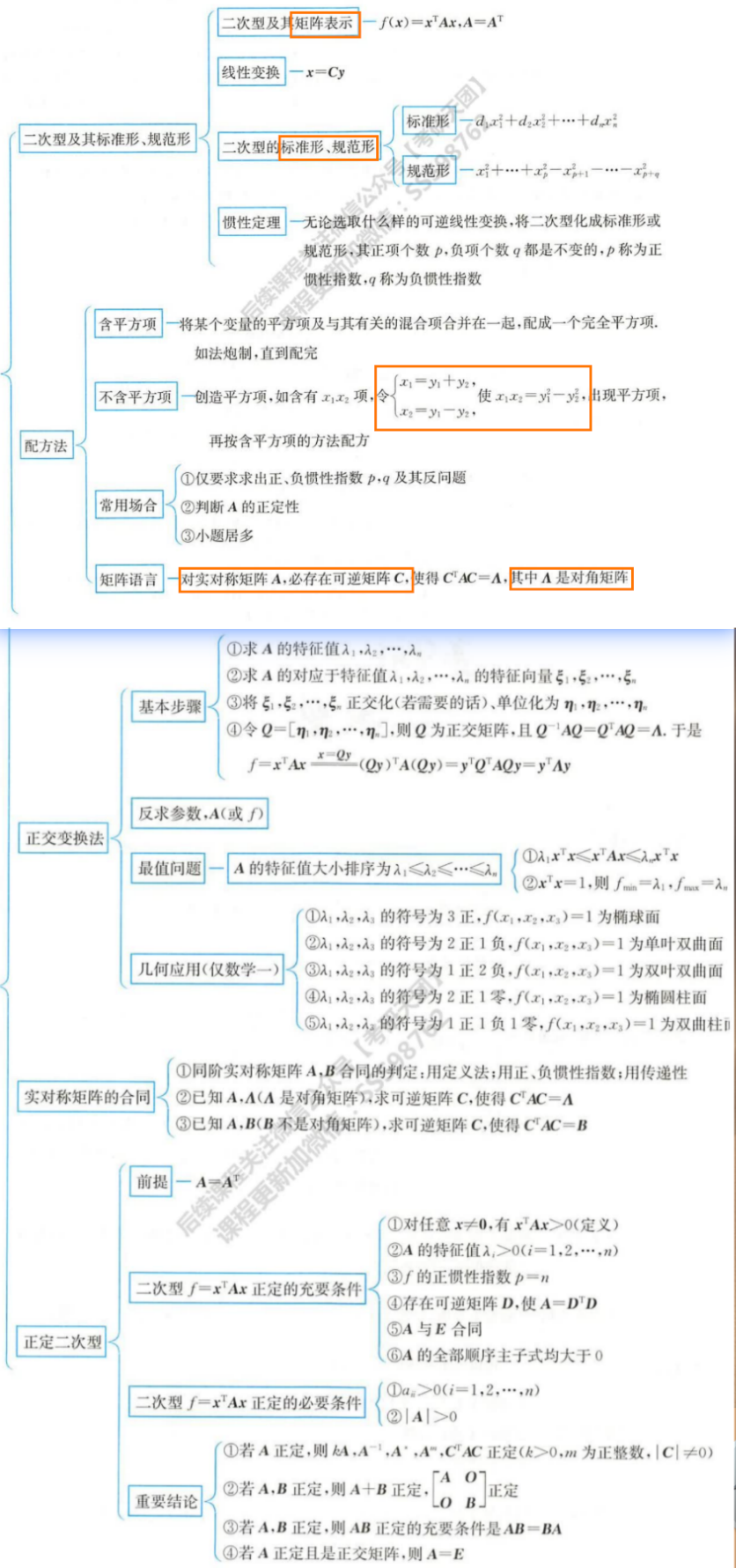
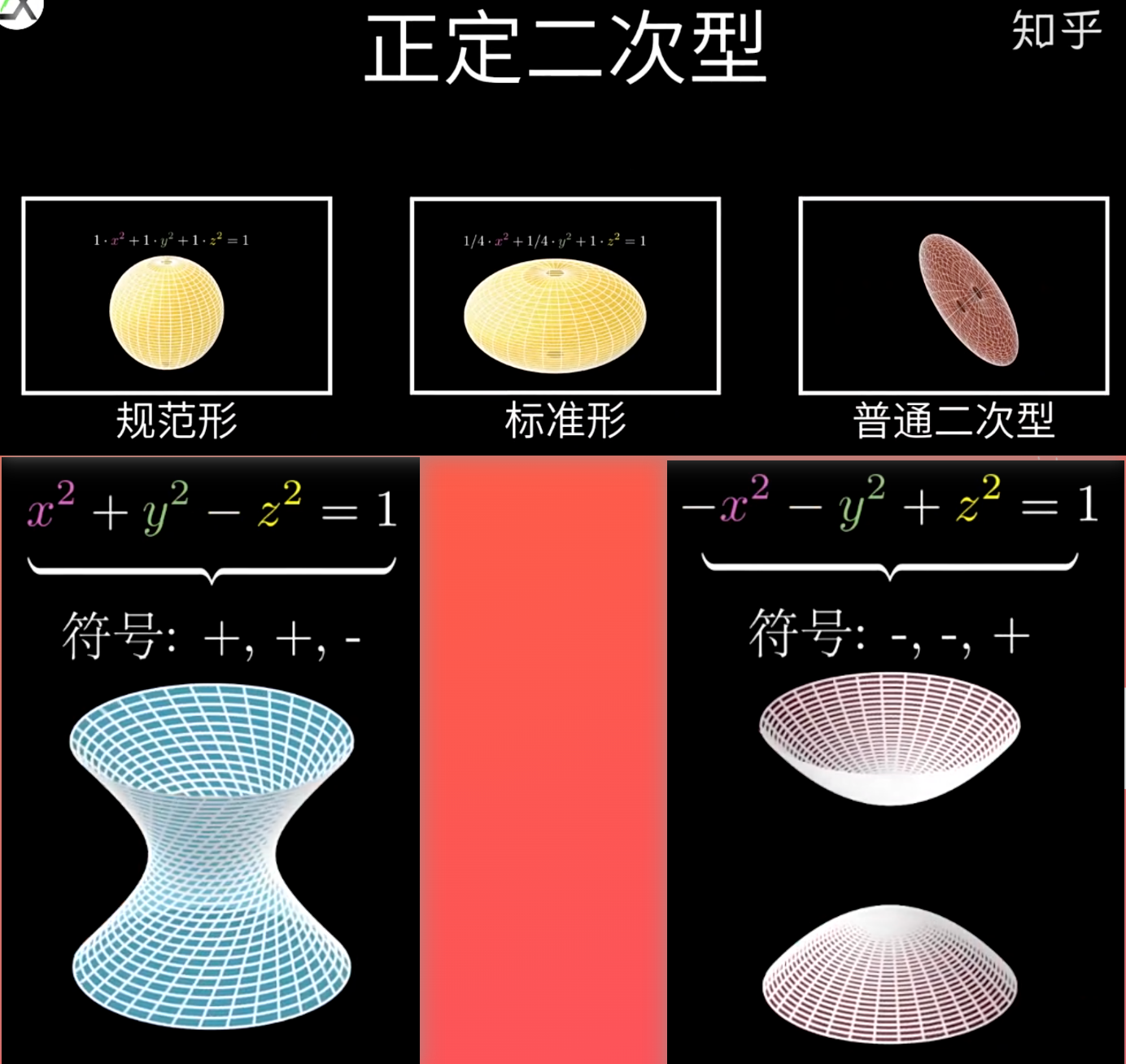
- 二次型是应用
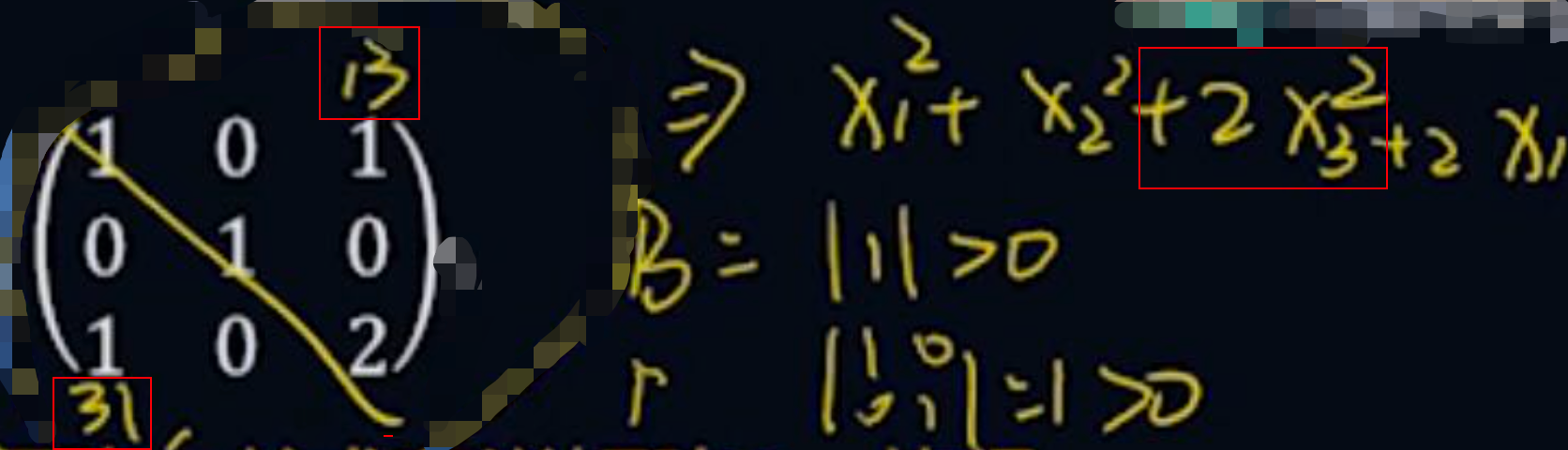
- 正定是描述二次型的->正定二次型
- 判断是否正定
- |A|:
- λ,α:
- 相似合同:
- C可逆,A=CTC
- CTAC=E;A与E合同
- 二次型:
- 定义:x=0,xTAx>0
- f的正惯性指数p=n

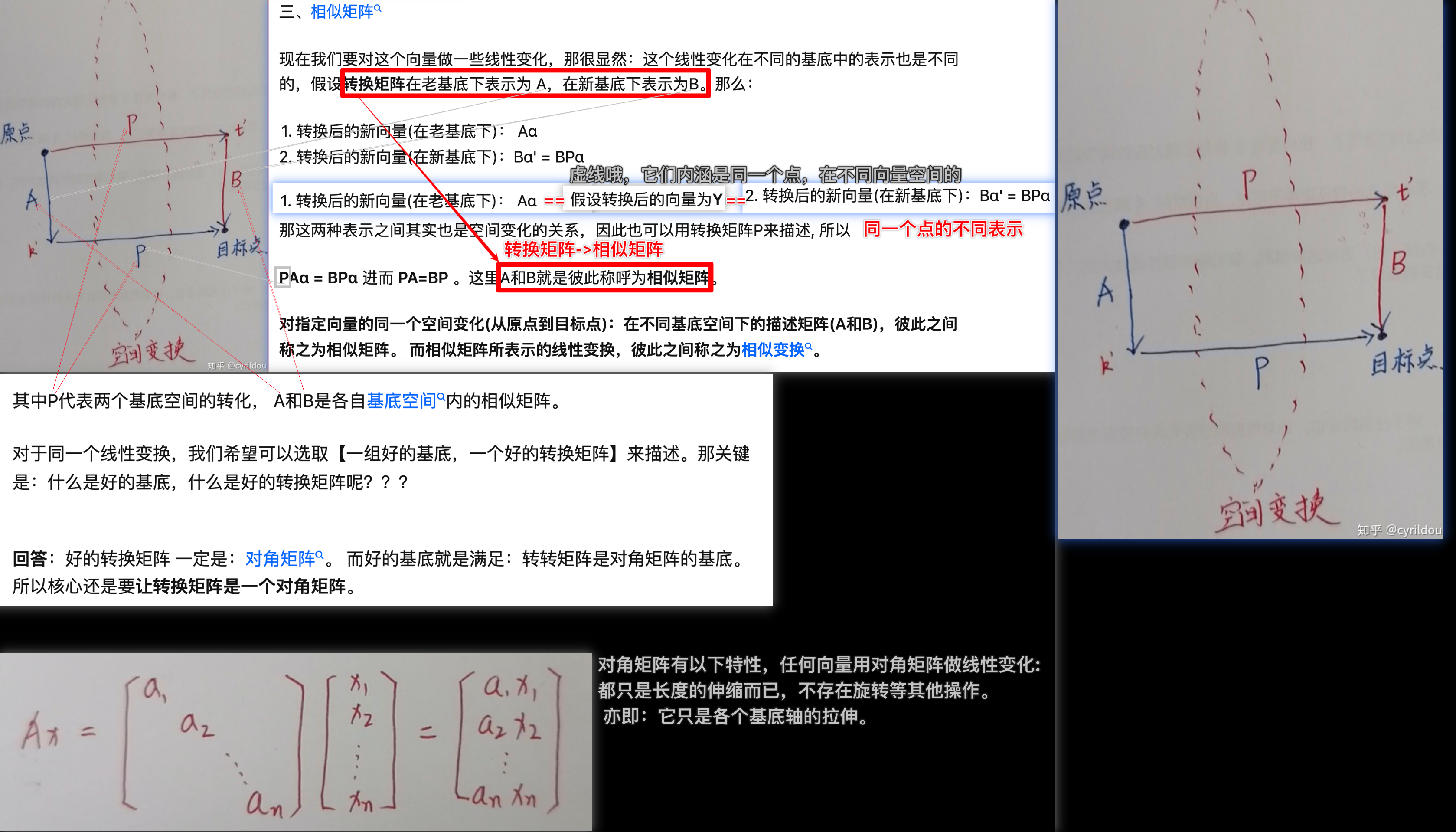
- 当要求相似关系的时候,一个重要的突破点;就是有n个向量无关的特征向量,而特征向量又是与特征值密切相关的,就是一般就是判断矩阵A的特征值。
- 当求A的特征值的时候,比较难,或者题目是抽象的,根本不能直接求出来,一个重要的思想就是f(A)=0; f(λ) = 0,进而求出A的特征值。
- A的秩为1,它的迹不等于0 ==> 可推出A能相似对角化。
- 秩为1,则A2=tr(A)∗A→f(A)=A2−tr(A)A=0→f(λ)=0→λ2−tr(A)λ=0→λ只能是0,tr(A)
- 由于 tr(A)=λ1+λ2+...+λn,所以A有n-1个0, 1个tr(A)的特征值。n重特征值有n个线性无关的特征向量,那么就能得证。
- 当f(A)=0;比如f(A)=A→g(A)=f(A)−A=0

- 2512
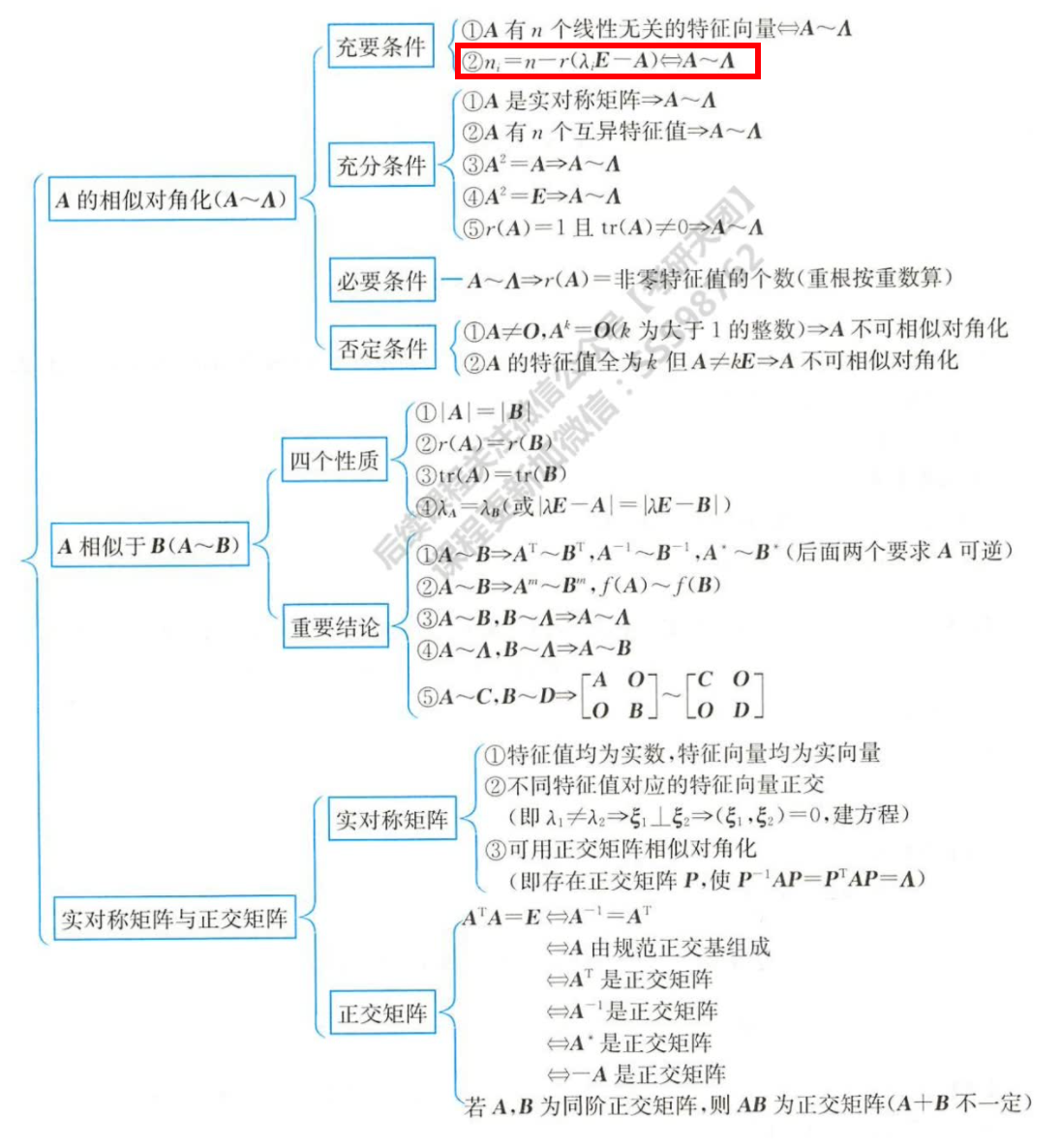
- 找出所有: λ
- 特征值 f(A)=0−>f(λ)=0
- 利用: ni=n−r(λiE−A)⇔A∼Λ
- 回归到: A 有 n 个线性无关的特征向量 ⇔A∼Λ
- 充分必要条件:
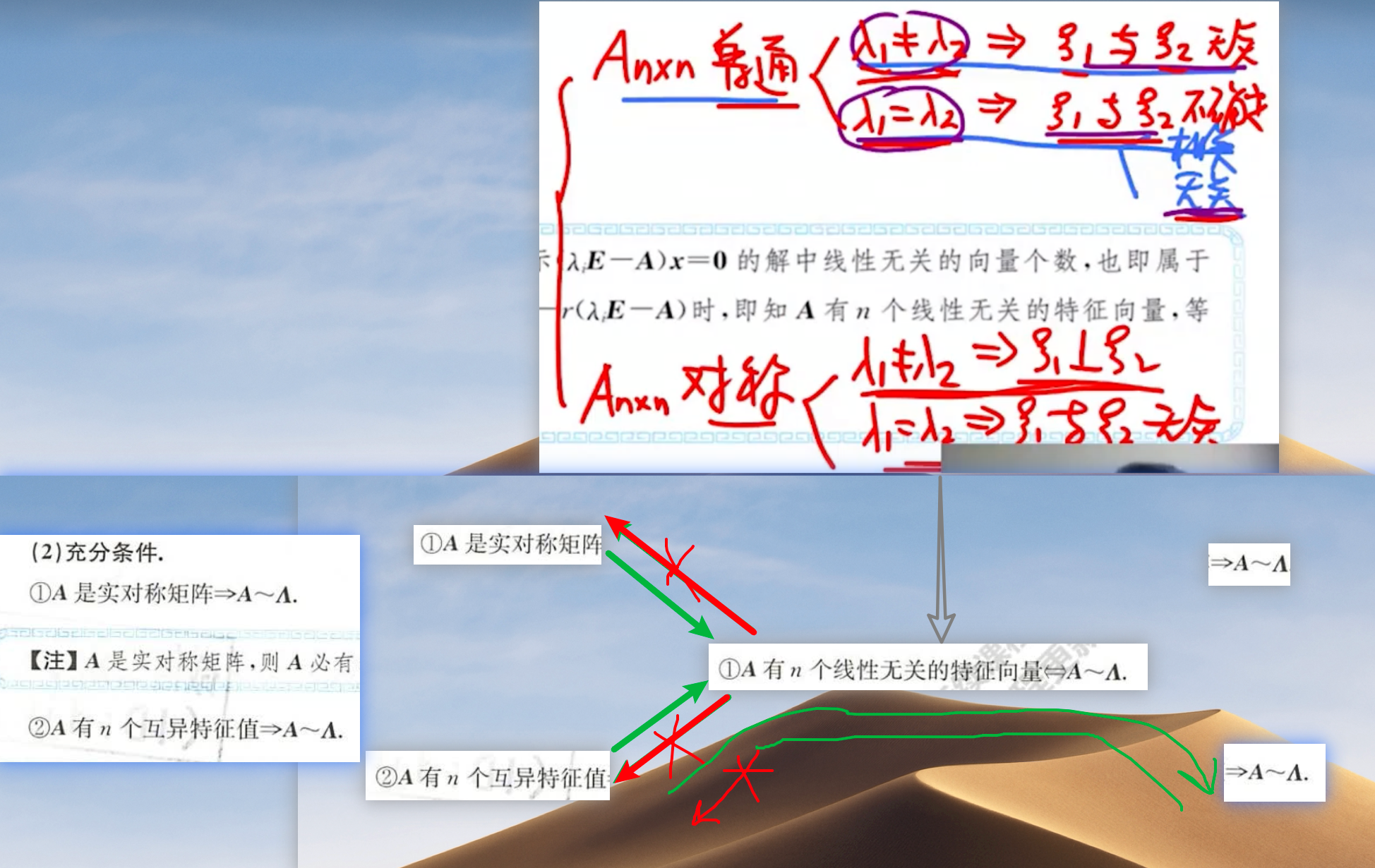

-
增加的充分条件:
-
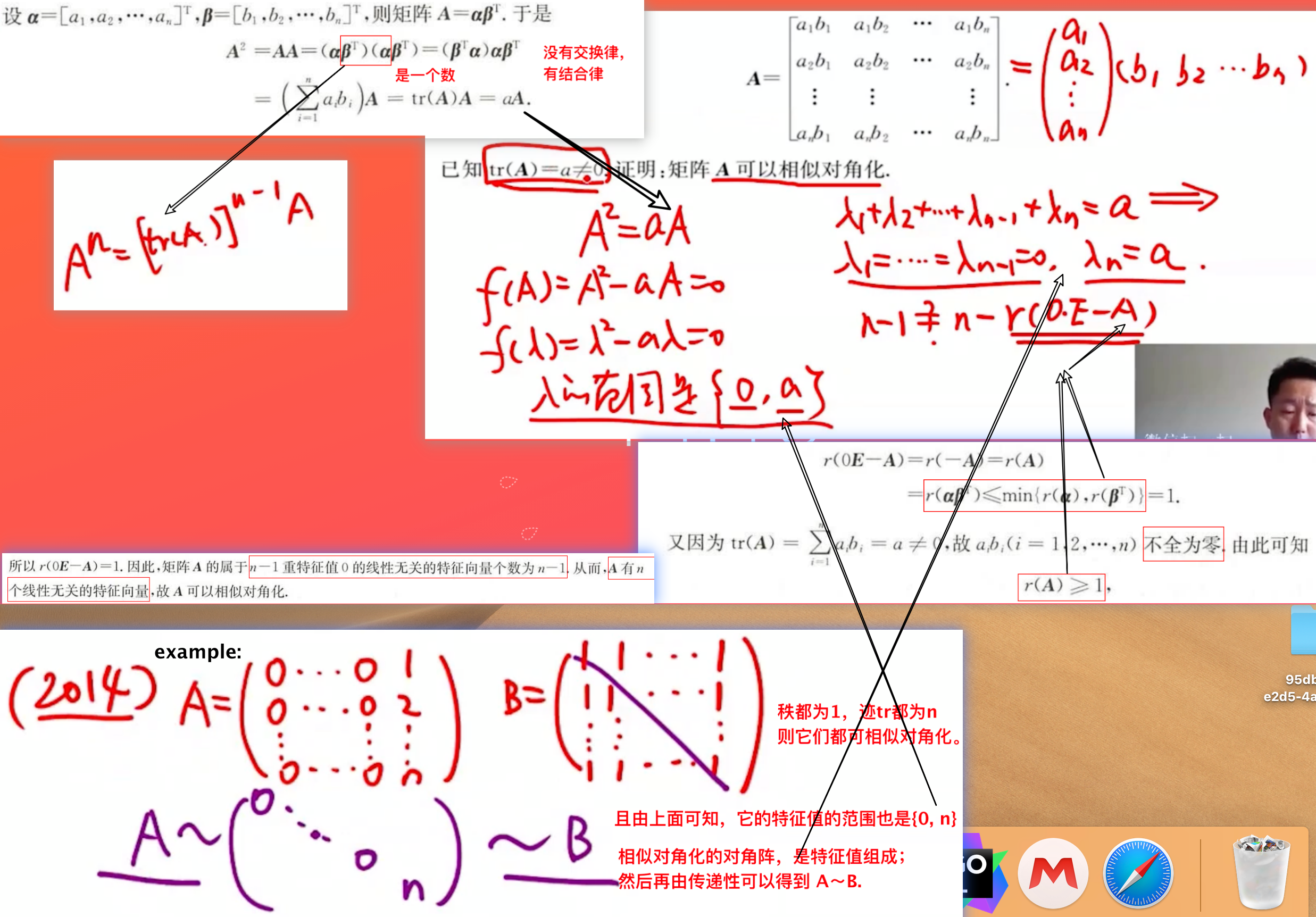
-
必要条件/否定条件:
- 四个必要不充分条件:

- AB相似的四个条件
- λA==λB

- r(A)==r(B)
- 重要结论:
-

-

- A∼Λ与B∼Λ中,Λ应该要相等。
-
实对称矩阵四条性质:
: 先说特征值->特征向量->有正交矩阵相似对角化(这里就包括了第三个性质)(特征向量之间必定线性无关)
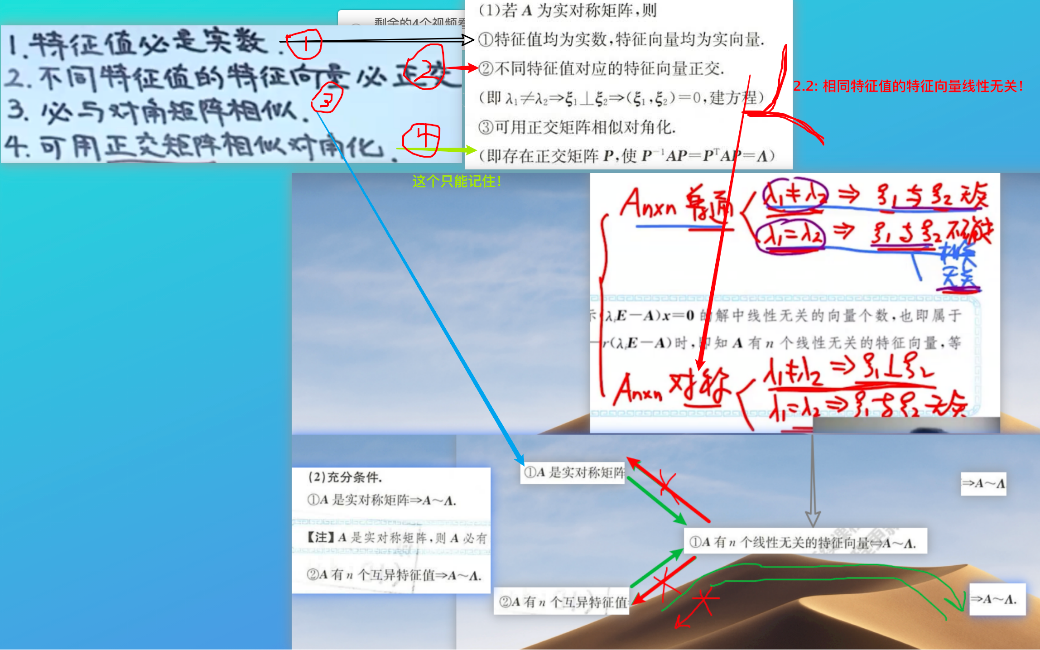
-
正交矩阵的二个性质:正交矩阵的转置-求逆-伴随都是正交矩阵
⎩⎨⎧ATA=E 若 A,B⇔A−1=AT⇔A 由规范正交基组成 ⇔AT 是正交矩阵 ⇔A−1 是正交矩阵 ⇔A∗ 是正交矩阵 ⇔−A 是正交矩阵 为同阶正交矩阵,则 AB 为正交矩阵 (A+B 不一定 )
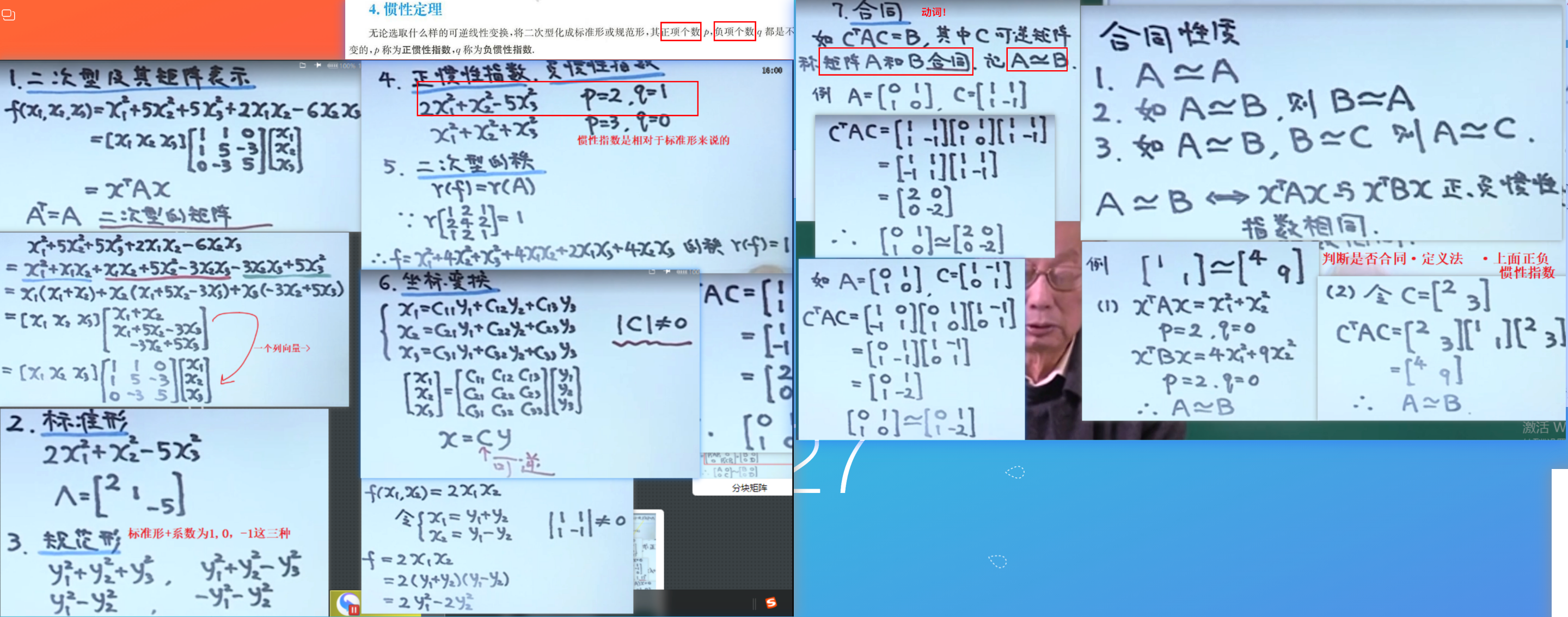
- 为什么是对称矩阵必有可逆矩阵C,使得CTAC=Λ, 其中 Λ 为对角矩阵?
- 实对称矩阵有正交矩阵C, C−1AC=CTAC=Λ
- 如何求齐次方程组的解?(求特征向量)
- 施密特正交化
β1=α1β2=α2−(β1,β1)(α2,β1)β1β3=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2
⎩⎨⎧β1=α1;β2=α2−(β1,β1)(α2,β1)β1β2=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2
-
在已知A和r(A)的前提下,求A∗,可以通过r(A)与r(A∗)来简化计算

-
∣A−λE∣=(−1)n∣λE−A∣=0
- ∣A−λE∣=∣λE−A∣
-
A与B在相似的环境的下(是实对称矩阵,在合同的环境下)
- A?之间的关系B : 一个很取巧的方式是通过中介:比如Λ
- Q⊤AQ=Λ1A=(Q⊤)−1Λ1Q−1 先翻转到一边,然后再代入其它式子里面
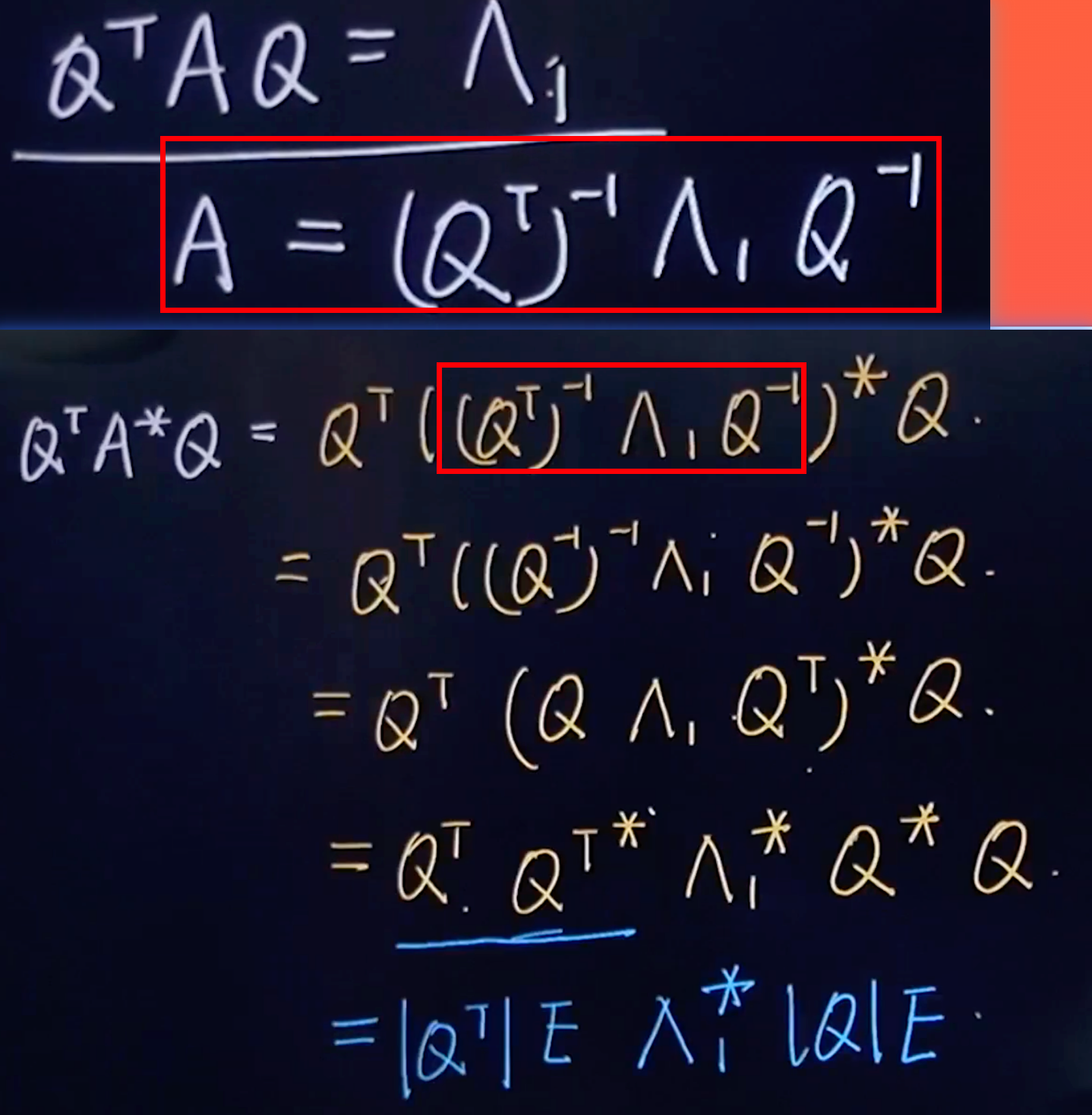
- 求A~B

- 相同的P, P−1AP,PTBP
- 从内到外易->从外到内难->所以从里面向外一层层剥开;也就是分解P,把P=QC
A~B,必要条件: 四个重要的等式


- E
- AAT=E
- AA−1=E
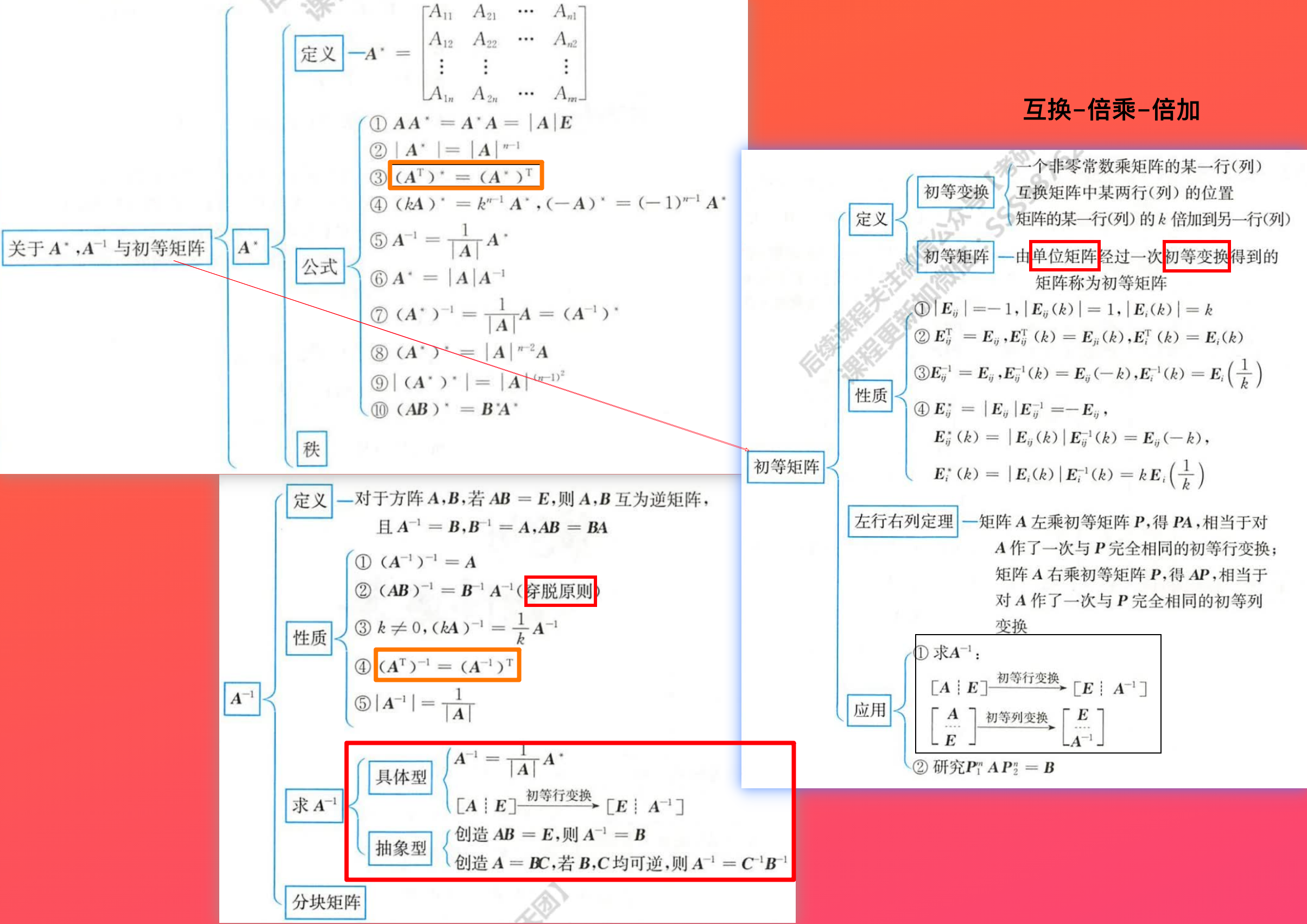
- 初等矩阵:

- Eij
- Ei(K)
- Eij(K): 第i行(列)∗K加到第j行(列)
- Eij(K): 第i行(列)∗K加到第j行(列)
- Eij−1(K): 第i行(列)∗K加到第j行(列),然后再取逆,它的结果与Exx(X)的关系
| . |
秩 |
转置T(想象一下三阶的单位矩阵(⚠️须是单位矩阵,其他矩阵是没有这个特性):ET=E−>如果不是倍加的情况,其他转置情况都不变) |
求逆-1 |
伴随* |
| Eij |
x |
x |
Eij |
| Ei(K) |
x |
x |
Ei(K1) |
| Eij(K) |
x |
Eji(K) |
Ei(−K) |
- 求逆-1: 想一想(A∣E)−>(E∣A−1)
- 伴随*: A∗=∣A∣A−1
⎩⎨⎧⎣⎡100010001⎦⎤−>Eij⎣⎡010100001⎦⎤−>T⎣⎡010100001⎦⎤−−−−−−−⎣⎡100010001⎦⎤−>Eij⎣⎡010100001⎦⎤
- 当P=E原始;;;当PA−>左行右列E原始A−>左行右列E12(1)⋅E2(−2)⋅E12(1)⋅E⋅A
- 方向是先化为行阶梯,然后反过来算对应的E_{xxx}
⎣⎡1101−10001⎦⎤−>化为阶梯形⎣⎡1001−20001⎦⎤−>⎣⎡100110001⎦⎤−>⎣⎡100010001⎦⎤⎣⎡1101−10001⎦⎤<−E12(1)⎣⎡1001−20001⎦⎤<−E2(−2)⎣⎡100110001⎦⎤<−E12(1)⎣⎡100010001⎦⎤E原始=E12(1)⋅E2(−2)⋅E12(1)⋅E

- 单独记忆A∗总是保持统一的,
- 比如(二): (kA)∗它的最终结果还是A∗乘以某个结果,跟(kA)−1=k1A−1,以A−1为本一样
- 比如(四): (A∗)∗它的最终结果还是A乘以某个结果,跟(A−1)−1=A相同,以A为本
- 比如(五): ∣A∗∣它的最终结果还是∣A∣为本,跟∣A−1∣=∣A∣1相同,以|A|为本
- (二),(三):
- (kA)−1=(kEA)−1=A−1(kE)−1=(kE)−1=k1Ek1A−1
- (kA)∗=(kEA)∗=A∗(kE)∗=(kE)∗=∣kE∣(kE)−1=kn(kE)−1kn−1A∗
- (一),(四):
- 互异,可以相互翻转
- 相同的,可以抵消(除了A∗)
- (A∗)∗=⎩⎨⎧∣A∗∣(A∗)−1∣A∗∣(A−1)∗∣A∣n−1∣A∣1A
- ∣A∗∣=∣∣A∣A−1∣=∣A∣n∣A−1∣=∣A∣n−1
- 相似/合同(合同引出二次型)的里面也有二个矩阵:
- 实对称矩阵的定义是:如果有n阶矩阵A,:

- 实: 其各个元素都为实数;
- 对称: 矩阵A的转置等于其本身(AT=A),则称A为实对称矩阵。
- 二次型矩阵一定是实对称矩阵
A可相似−>P为正交对角化A一定是实对称矩阵?
- 先假设一个A可以相似对角化(普通),那么就有 P−1AP=Λ(为对角阵)⟶A=PΛP−1
- 所以AT=A=PΛP−1(PΛP−1)T=(P−1)TΛTPT============================再假设P正交对角化,因为正交矩阵的性质,PPT=E,所以P−1=PTPΛP−1⟶AT=A,那么A一定是对称的。得证,A一定是对称矩阵
- 实对称矩阵A和B相似的充要条件是A和B有相同的特征值;
- 相同特征值表明“重数相等”;
- AB特征值相同则相似于同一个对角矩阵,根据相似的传递性,A相似与B。
- 正交矩阵: n阶方阵A, ATA=E ⟶AT=A−1
- 判断合同:
- 用定义法:A,B合同⇔存在可逆矩阵C,使得CTAC=B.
- 用正、负惯性指数: A,B合同⇔pA=pB,qA=qB.(相同的正、负惯性指数)
- 同阶实对称矩阵 A,B相似必合同;
- A=AT;B=BT,且A~B
- 实对称矩阵A,B相似⟶因实对称矩阵→必定可以相似对角化有相同的特征值/特征向量⟶⟶⟶⟶⟶⟶⟶⟶pA=pB,qA=qB(相同的正负惯性指数⇔A,B合同)A,B必合同
- 用传递性: A合同于C,C合同于B,则A合同于B.

- 初等变换
- define:三种基本的变换
- nature:
- 初等行变换不改变矩阵的秩:(矩阵的秩:向量的角度-矩阵的角度)
- 因为对矩阵做初等行变换,就相当于对齐次线性方程组做同解变换。而方程组同解时,当然它的秩(即独立方程的个数)就不会变。
- 一开始学秩的时候就觉得应该用独立方程个数来定义,不明白为什么还要引进一个非零子式的最高阶数
- application:
- 左行右列:可以求An
- A−1: (AE)⟶作初等变换(EA−1)
- 行阶梯
- 每一非零行都在每一零行之上。
- 某一行的先导元素所在的列位于前一先导元素的右边。
- 某一先导元素所在列下方元素都是零。
- 行最简:若一个阶梯形矩阵还满足一下性质,则称它为简化阶梯形(或简化行阶梯形)矩阵。
- 每一非零行的先导元素是1.
- 每一先导元素1是该元素所在列的唯一非零元素。
- 非零子式

把它向量组合起来,当成一个矩阵,然后想象成一个方程组形式
- 向量的维度代表方程的个数
- 向量的个数代表方程的未知数的个数
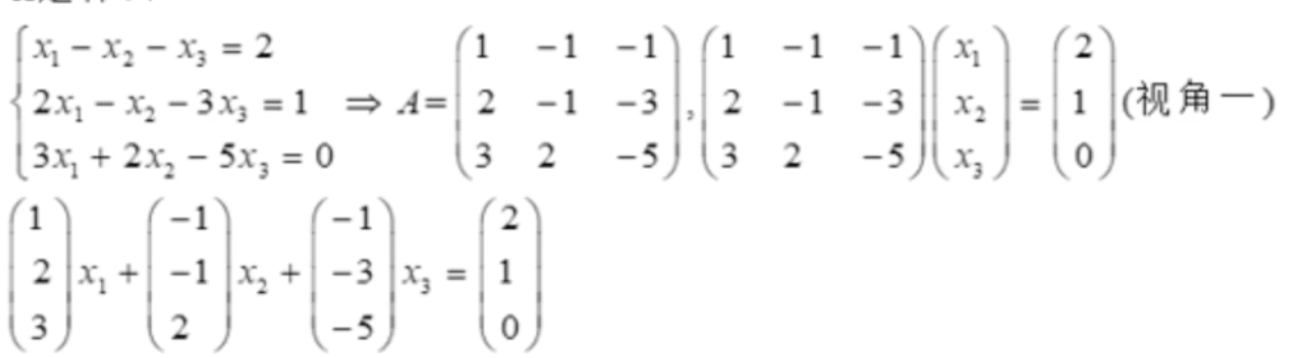
方程组研究对象
向量是研究方程的理论。
行列式/矩阵 研究工具
行列式一个数。核心是如果求这个数。并且这个数代表的含义是什么?
特征值/二次型应用。
https://pan.baidu.com/disk/pdfview?path=%2F考研%2F强化%2F线代指导%2F2022张宇考研数学线代9讲.pdf&size=84363937&fsid=183295534477322
李林: https://www.bilibili.com/video/BV1CR4y1J7fx?p=2
https://pan.baidu.com/play/video#/video?path=%2F考研%2F强化%2F05.2022强化专项特训%2F02.2022线代强化%2F15.第5讲线性方程组03.mp4&t=14
https://account.chsi.com.cn/passport/login?entrytype=applystu&service=https%3A%2F%2Fyz.chsi.com.cn%2Fapply%2Fj_spring_cas_security_check%3Bjsessionid%3D3BC4179936F13E60D01441DBA239E0BD
https://pan.baidu.com/disk/pdfview?path=/考研/强化/线代指导/2022张宇考研数学线代9讲.pdf&size=84363937&fsid=183295534477322

副对角行列式的由来:
不是第一行是(-1)(n+1),最后一行是(-1)(1+1),所以不应该是(-1)^{n(n+3)/2}?
(−1)n(n+3)/2=(−1)n(n−1)/2+2n=(−1)n(n−1)/2
一个结果。
你是用的思路是行列式展开定理
我是用的行列式定义算的,用逆序数判断的正负号
行列式每项都包括各行各列一个元素.
观察发现,第一行只能取最后一个数,第二行取倒数第二个数……
所以这样的行列式只有来自副对角元素乘积的一项,
正负号通过列的逆序数判断,τ(n,(n-1),(n-2)……3,2,1)=n(n-1)/2
所以副对角线以上都为零的矩阵的行列式=(-1)^n(n-1)/2乘以所有副对角元素
- 对于方阵A,B,若AB=E,则A,B互为逆矩阵,且A−1=B,B−1=A,AB=B
- (1)(A−1)−1=A.
- (2)(AB)−1=B−1A−1(穿脱原则).
- (3)k=0,(kA)−1=k1A−1.
- (4)(AT)−1=(A−1)T.
- (5)∣∣A−1∣∣=∣A∣1
逆序:(5,4)5>4,则他们是一个逆序
逆序数:(4,2,1,6,3,5)= 3+1+0+2+0
- 4的逆序有:(4,2),(4,1),(4,3)
- 2的逆序有:(2,1)
- ...
- 点积(Dot Product)又称数量积,是一个接受两个等长度的数字序列(通常是向量坐标),然后返回单个数字的代数运算。在欧几里德几何中,两个笛卡尔坐标向量的点积常称为内积(Inner Product)。
(1) 0⩽r(Am×n)⩽min{m,n} (2) r(kA)=r(A)(k=0) (3) r(A)=r(PA)=r(AQ)=r(PAQ) (4) r(AB)⩽min{r(A),r(B)} (5) r(A+B)⩽r([A,B])⩽r(A)+r(B) (6) r([AOOB])=r(A)+r(B) (7) r(A)+r(B)⩽r([ACOB])⩽r(A)+r(B)+r(C) (8) r(AB)⩾r(A)+r(B)−n (9) r(A)=r(AT)=r(AAT)=r(ATA) (10) r(A∗)=⎩⎨⎧n,1,0,r(A)=nr(A)=n−1r(A)<n−1(11)若A2=A,则r(A)+r(A−E)=n(12)若A2=E,则r(A+E)+r(A−E)=n(13)Ax=0的基础解系所含向量的个数s=n−r(A)(14)若A∼Λ,则ni=n−r(λiE−A),其中λi是ni重特征根(15)若A∼Λ,则r(A)等于非零特征值的个数,重根按重数算
-
\beta2=\belta1+\frac{(\belta1,\alpha2)}{(\alpha2,\alpha2)}\alpha2
-
\beta3=\belta+\frac{(\belta1,\alpha2)}{(\alpha2,\alpha2)}\alpha2
-
∣kA∣=kn∣A∣⎩⎨⎧(kA)⊤=kA⊤(kA)∗=kn−1A∗(kA)−1=k1A−1
- 定义 A*B=E
- A−1=∣A∣1A∗
- 可逆矩阵一定可以经过若干次初等行变换,化为同阶的E. (A∣E)→(E∣A−1)