离散数学
数理逻辑
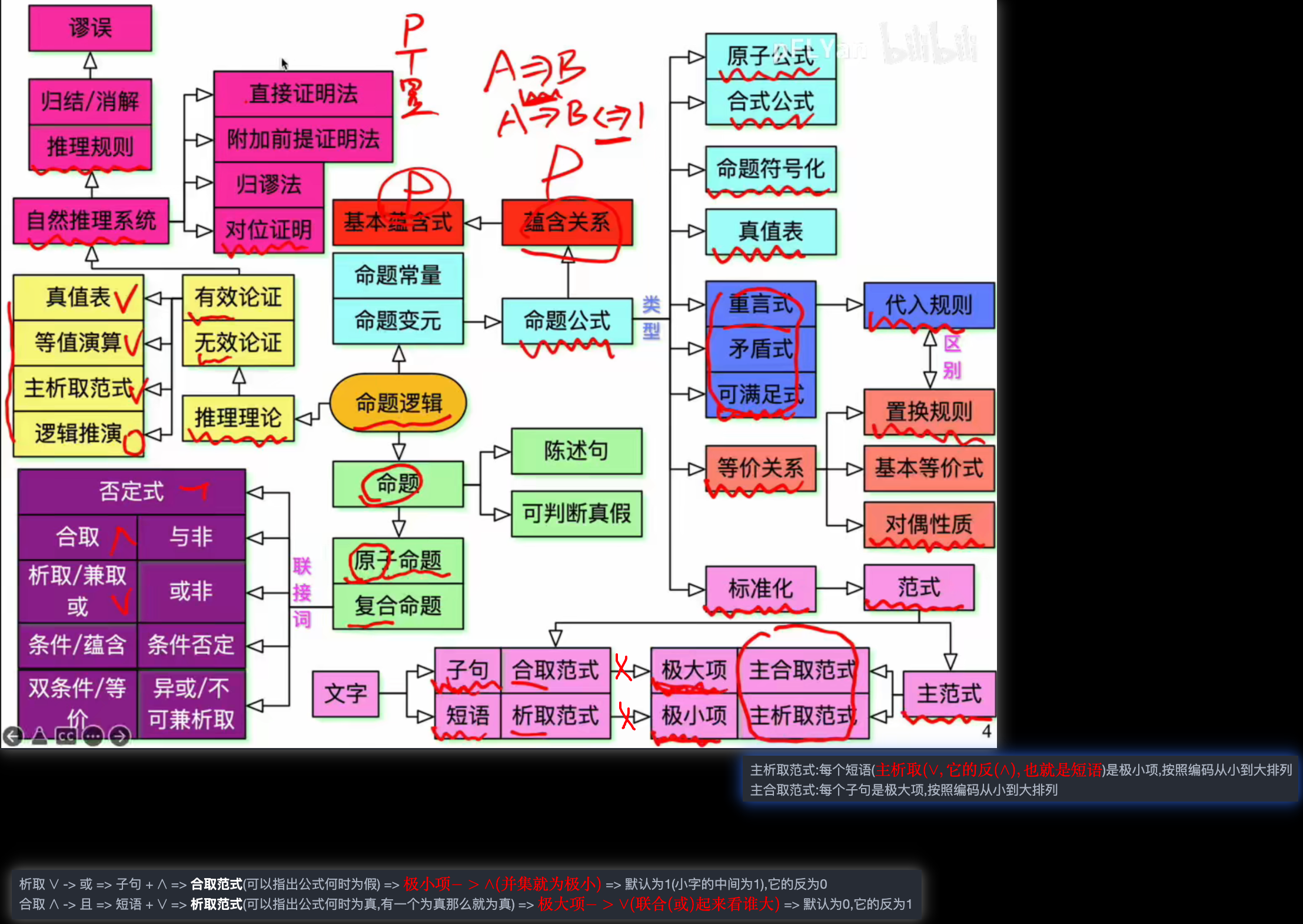
命题逻辑
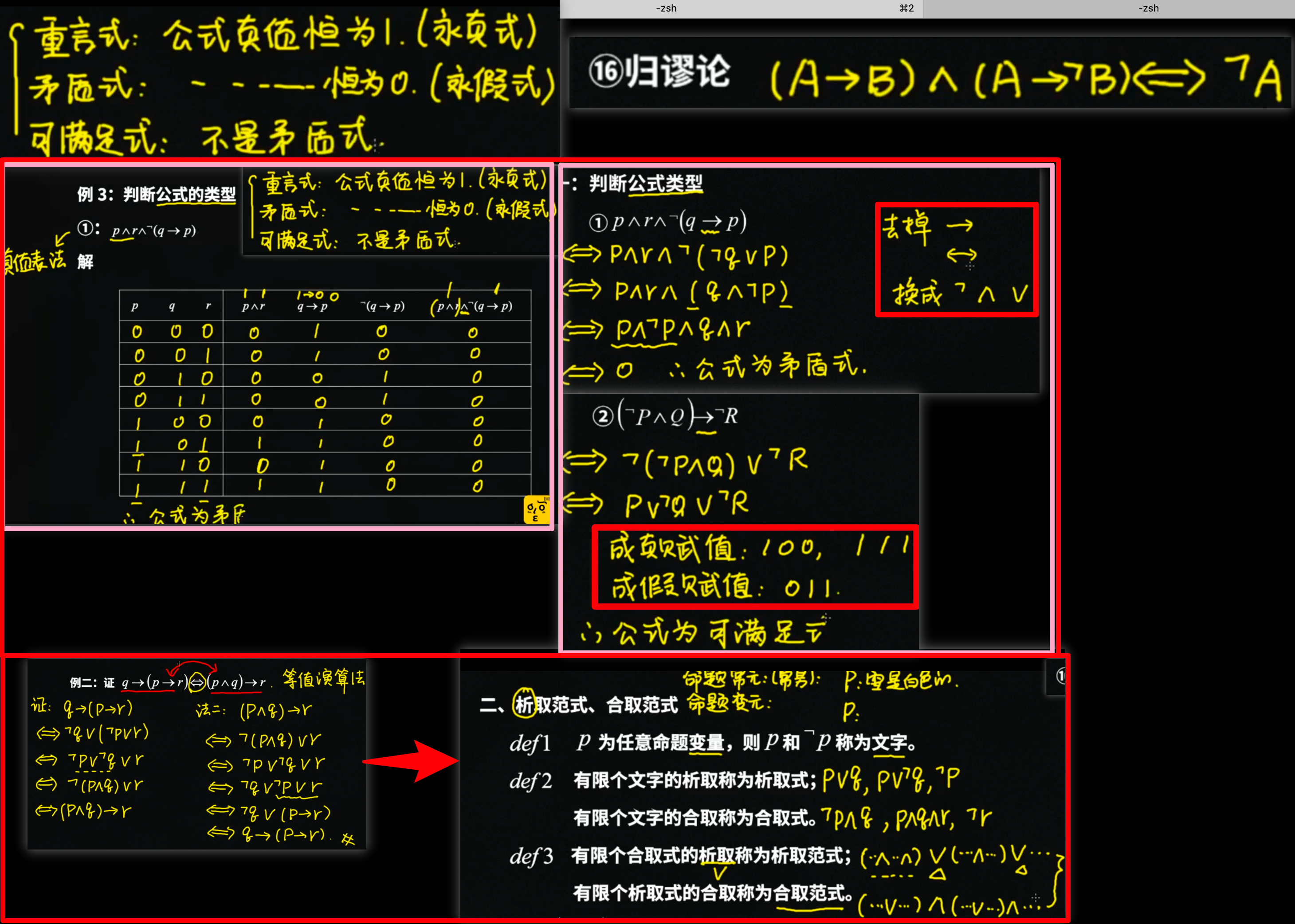
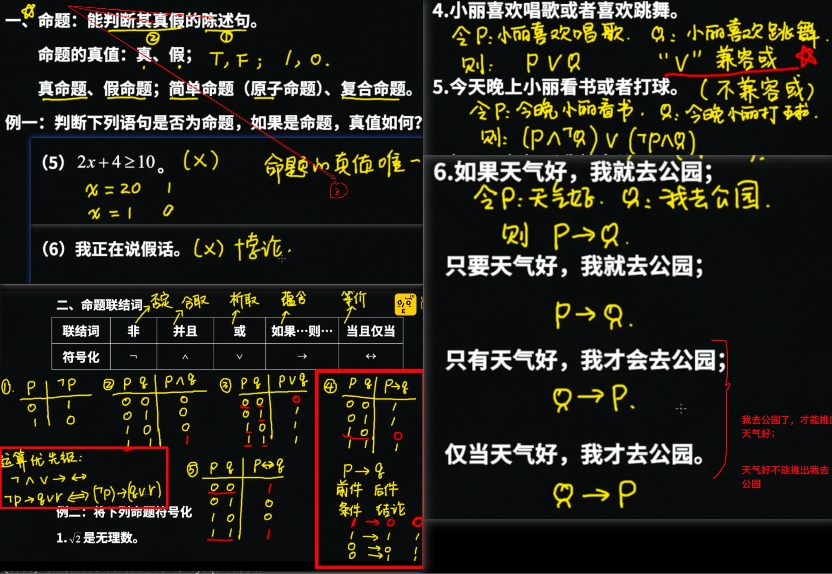
- 析取 -> 或 => 子句 + => 合取范式(可以指出公式何时为假) => => 默认为1(小字的中间为1),它的反为0
- 合取 -> 且 => 短语 + => 析取范式(可以指出公式何时为真,有一个为真那么就为真) => => 默认为0,它的反为1
- 主析取范式:每个短语()是极小项,按照编码从小到大排列
- 主合取范式:每个子句是极大项,按照编码从小到大排列
-
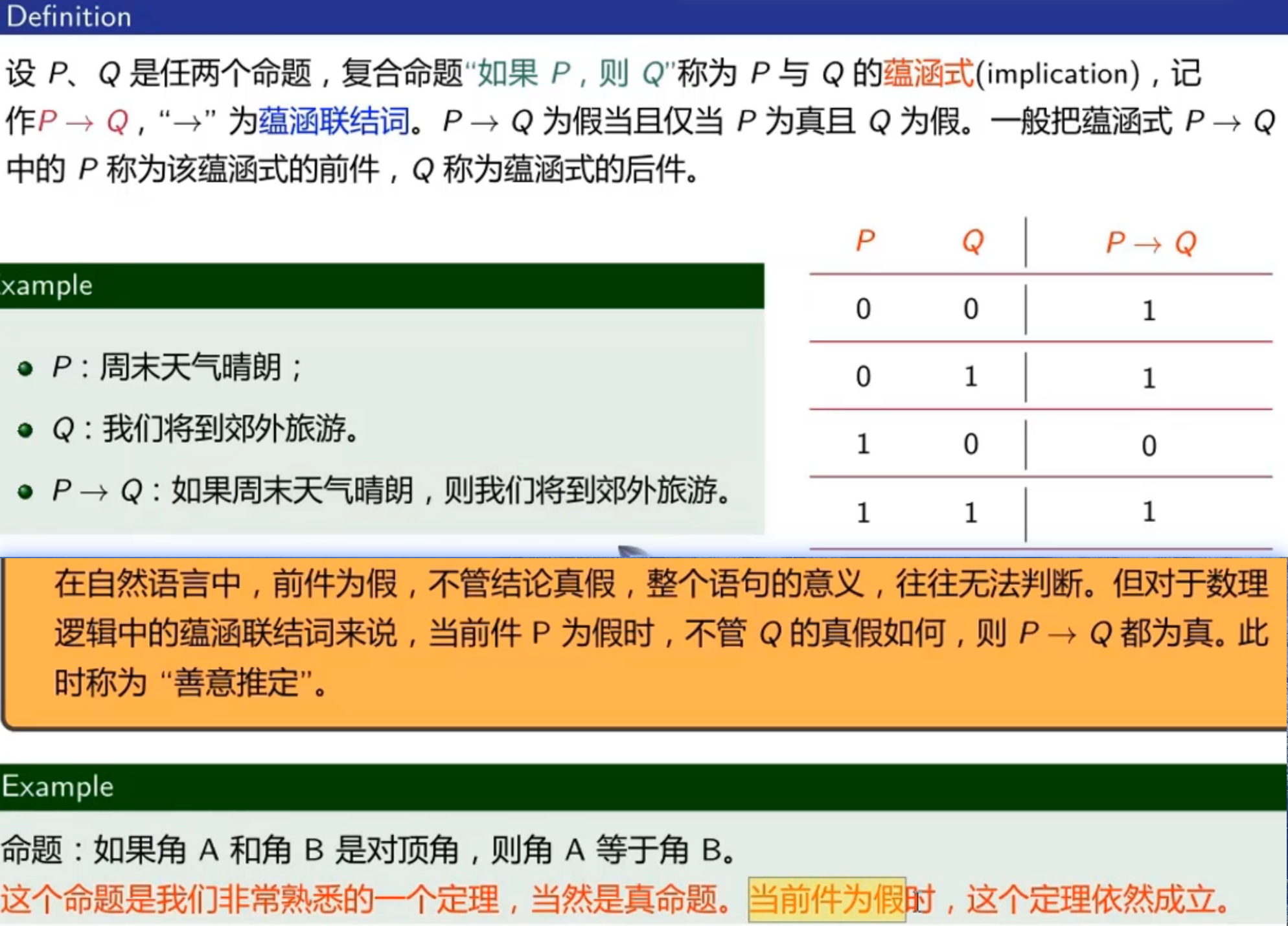
判断蕴含的真假
-
极大/极小的编码方式记忆,成假/真
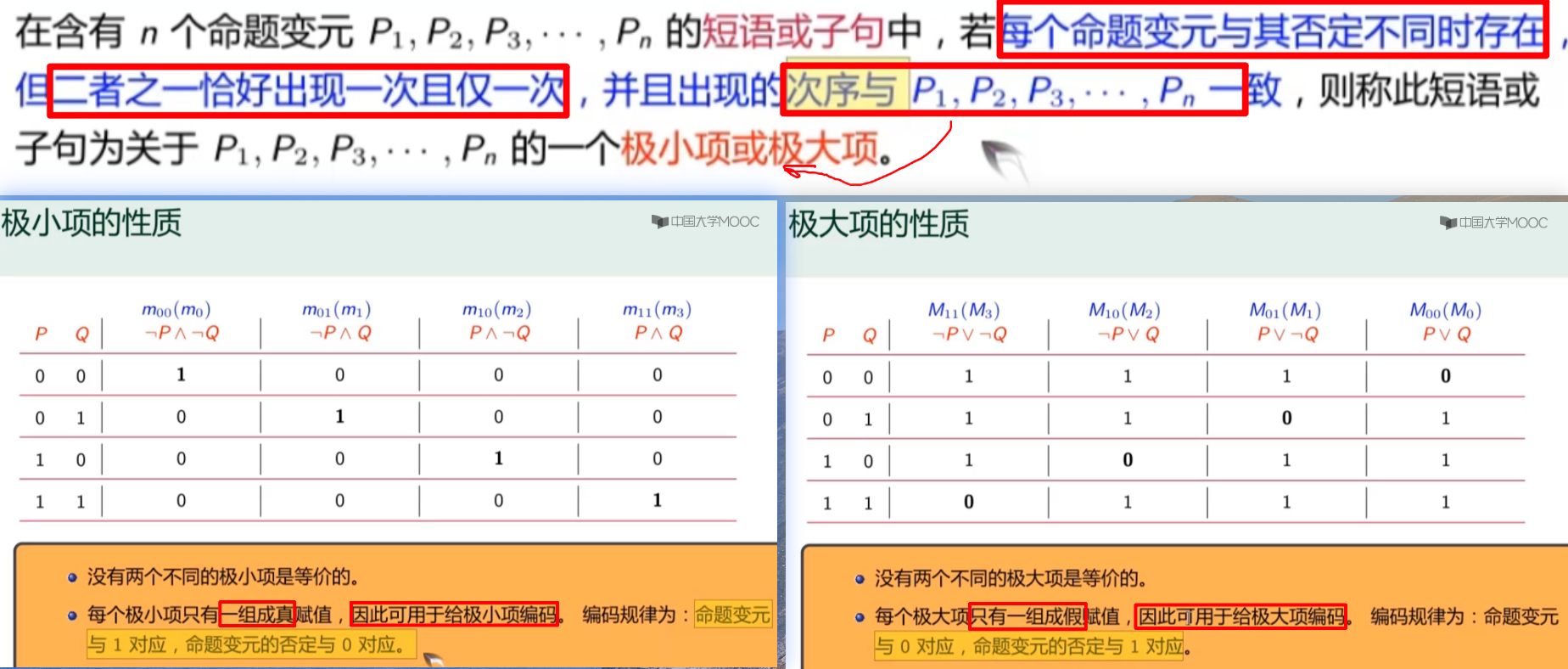
- 极大项是让它真值结果为假,要让它析取为假,需让它每一项为假,
- 极大项是让它真值结果为假,要让它析取为假,需让它每一项为假,
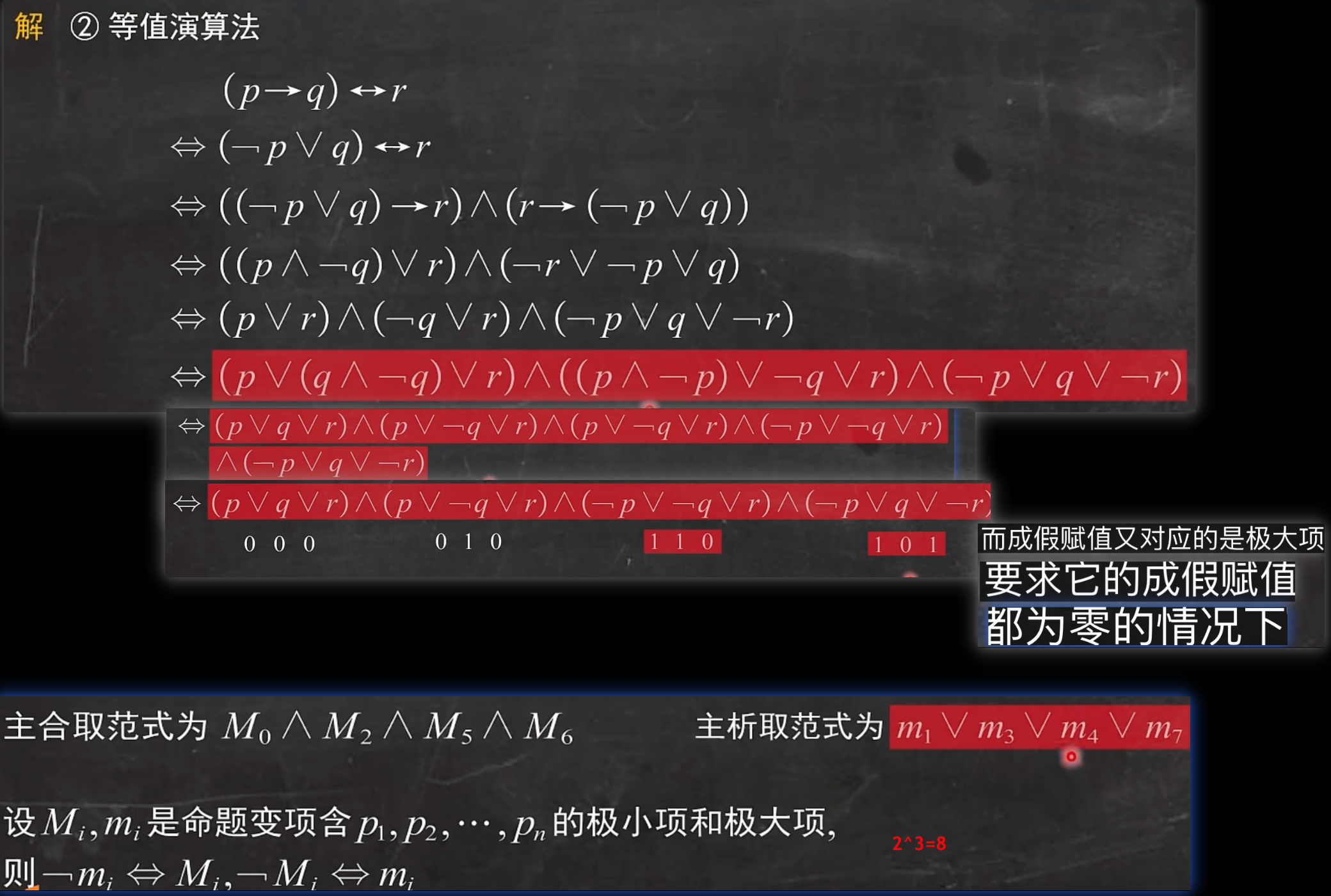
求主析取/合取范式
真值表发
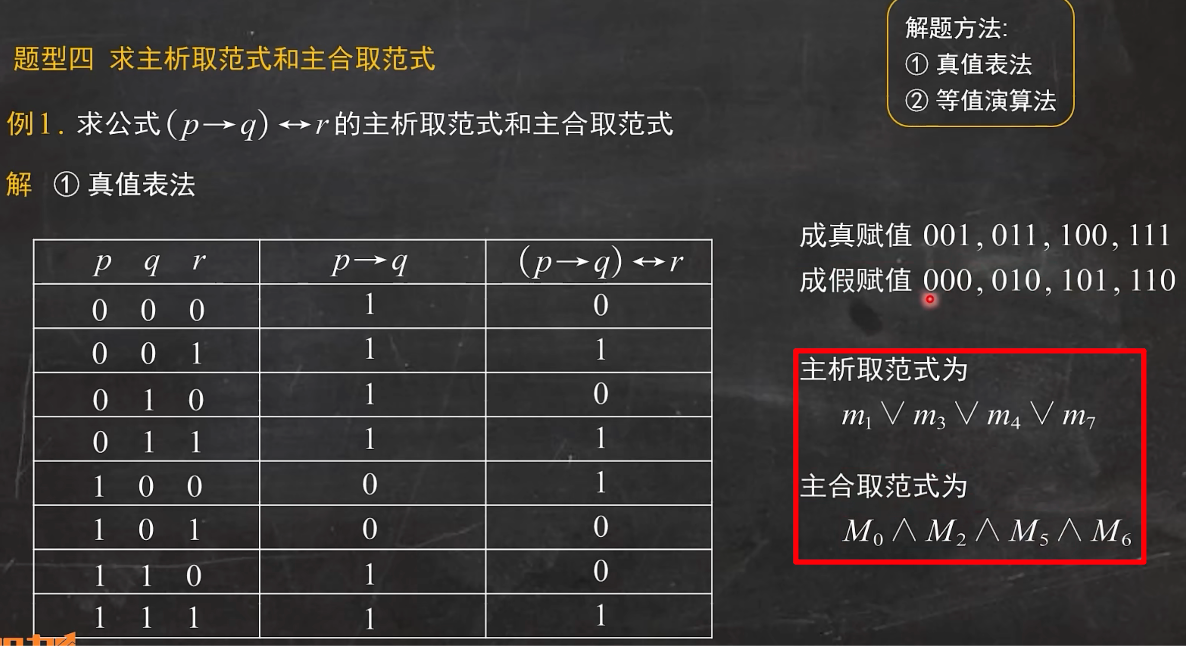
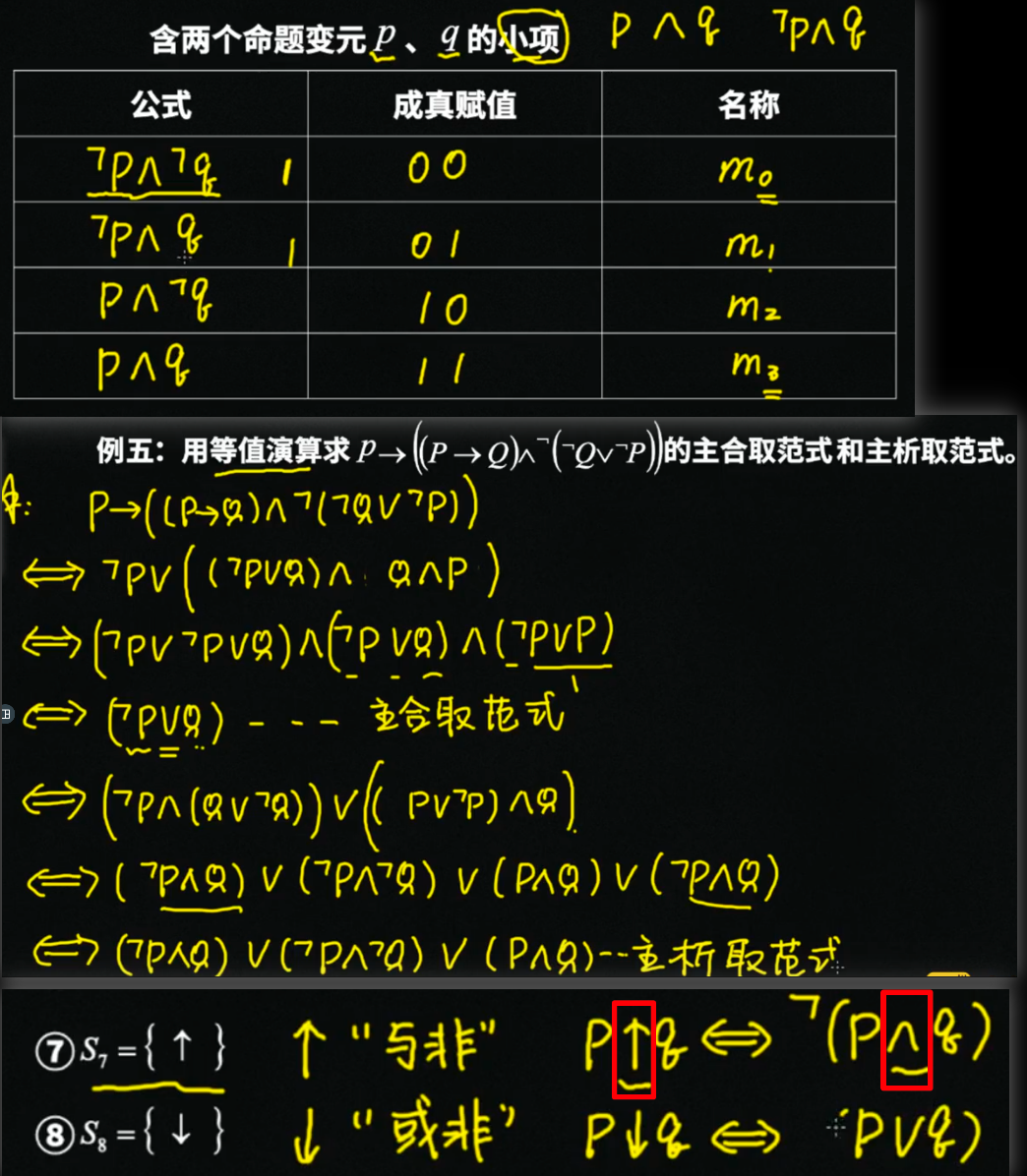
- 极小项<=>合取
- 极大项<=>析取
- 成真赋值 合取 => 极小项
- 成真赋值 => 合取 主析取范式
等值演算法
当缺P的公式中,其他项之间是用 ; 那么需要加 (零)
当缺P的公式中,其他项之间是用 ; 那么需要加 (一)
谓词逻辑
-
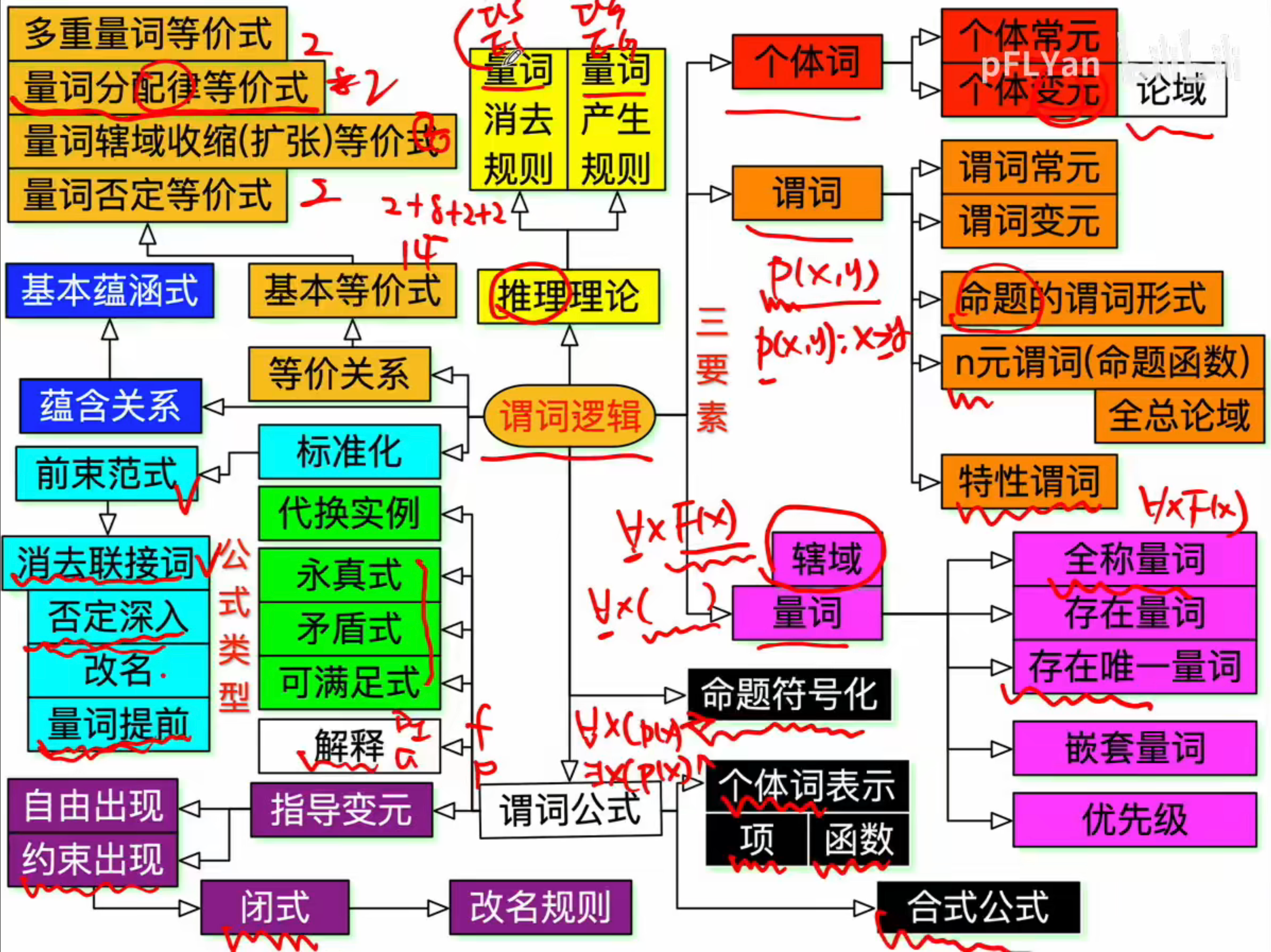
-
P(x,y), P才是谓词
-
全称/存在量词。
证明法
证明的基本工具
- 等价
[=]变形(E) - 推理
也叫蕴含[=>](I)nfer:- 如果所有前提的合取为真,则结论为真,如果
GvH为真,则G或H有一个为真, 为真,则G为假,则H为真 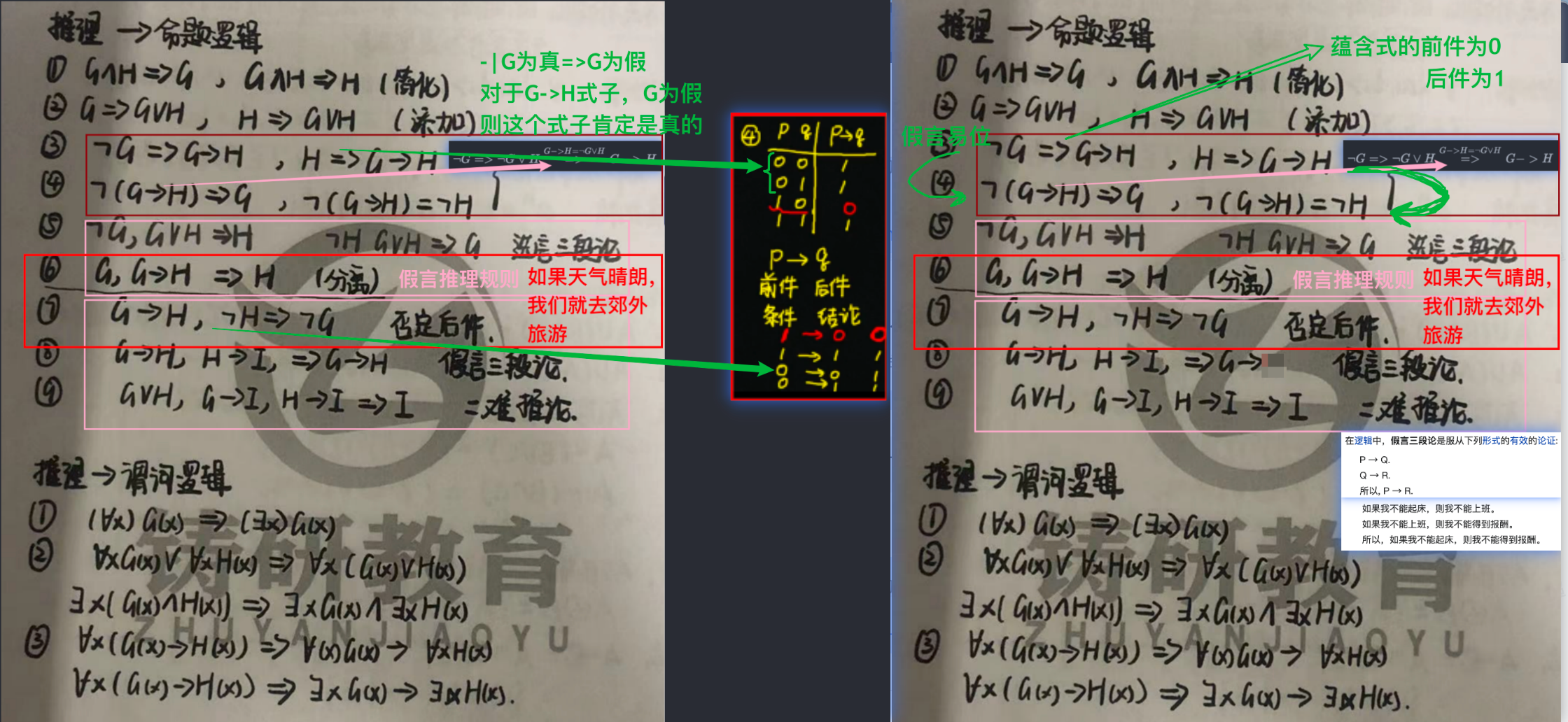
- 如果所有前提的合取为真,则结论为真,如果
- 推理规则:US,ES,UG,EG
- US(全称指定规则 Universal Specify)
- ES(存在指定规则 Exstential Specify)
- UG(全称推广规则 Universal Generalize)
- EG(存在推广规则 Existential Generalize)
- P(Premise)规则:就是直接利用推理中给出的前提,即前提引入。
- T(Transformation)规则:就是由某一个或几个前提可以通过等价、蕴含得到其他命题公式,即推理规则。
- I表示在T规则中通过蕴含式推出其他命题公式,即推理规则中的蕴含推理。
- E表示在T规则中通过等价式推出其他命题公式,即推理规则中的置换(等价)规则。
- CP(Conclusion Premise)规则即附加前提引入,在最后使用。
- 如能从给定的前提集合C与公式P推导出S,则能从此前提集合C推导出
- →与⇒
- 命题逻辑中的"→"符号表示了一个命题。比如说p→q,代表的是我们在给出命题"p→q"时,目的就是为了去判别命题的真假。(或者以此命题为依据来判别其他命题的真假)
- 而数学中的"⇒"符号表示了一个对事实的陈述,意思就是当我们说"p⇒q"时相当于断言
- 而我们使用"⇒"符号是为了以"p→q"这个已经被证明过的命题为前提,去判断p或q的真实性,而不是去研究命题本身的真值。
证明方式
演绎法
-
- 消去量词
- 那么它的量词的消去有顺序?是的,先用ES在用US.
-
- 无量词
- 使用基本等价公式,基本蕴含公式
-
- 添加量词
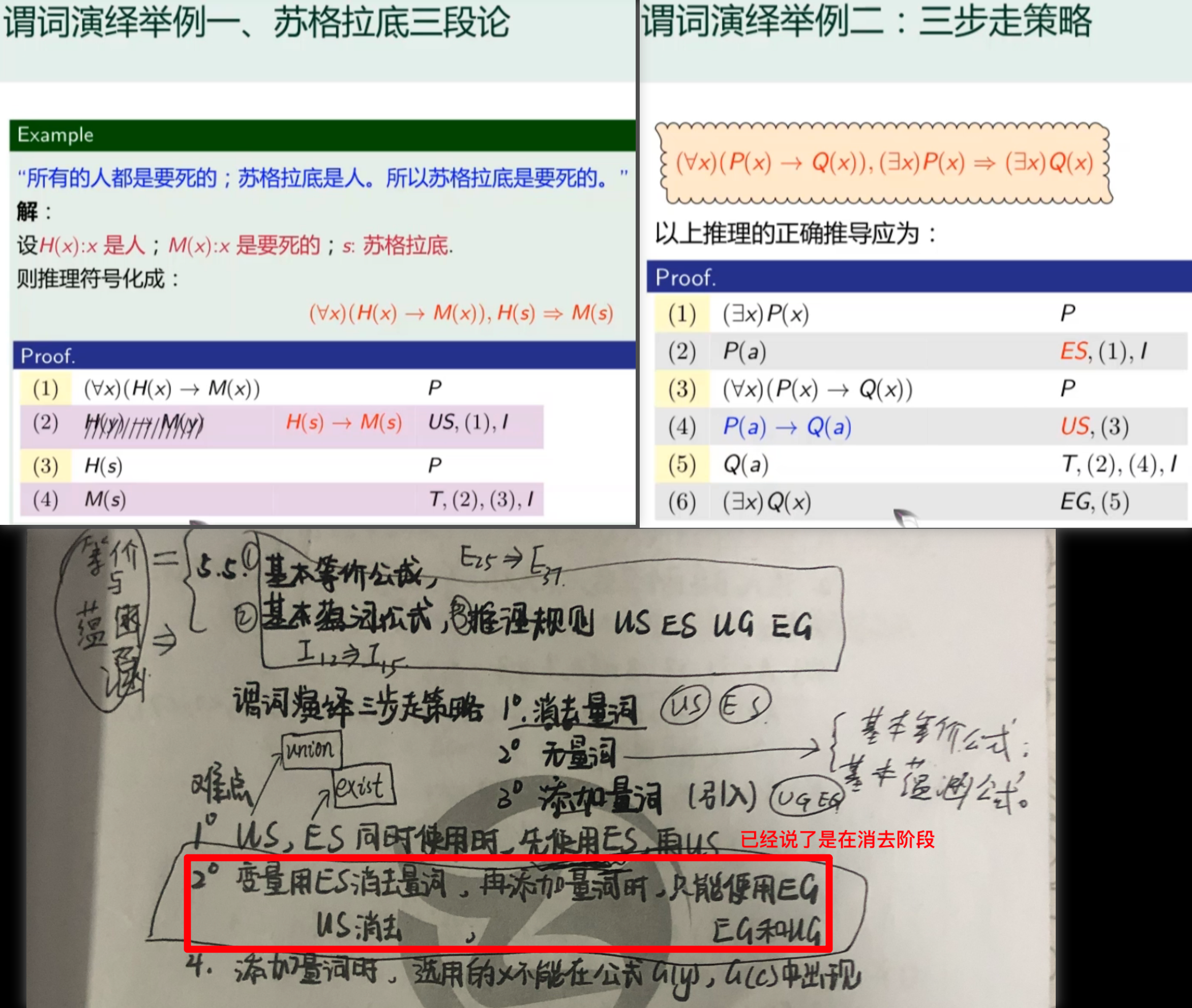
CP规则
- CP(Conclusion Premise)规则即附加前提引入,在最后使用。
- 如能从给定的前提集合C与公式P推导出S,则能从此前提集合C推导出

反证法
前束范式
-

- 首先去除蕴含等值(使用蕴含式 )
- 然后使用量词否定等值
- 换名规则;
- 最后辖域扩张/收缩;
-

函数
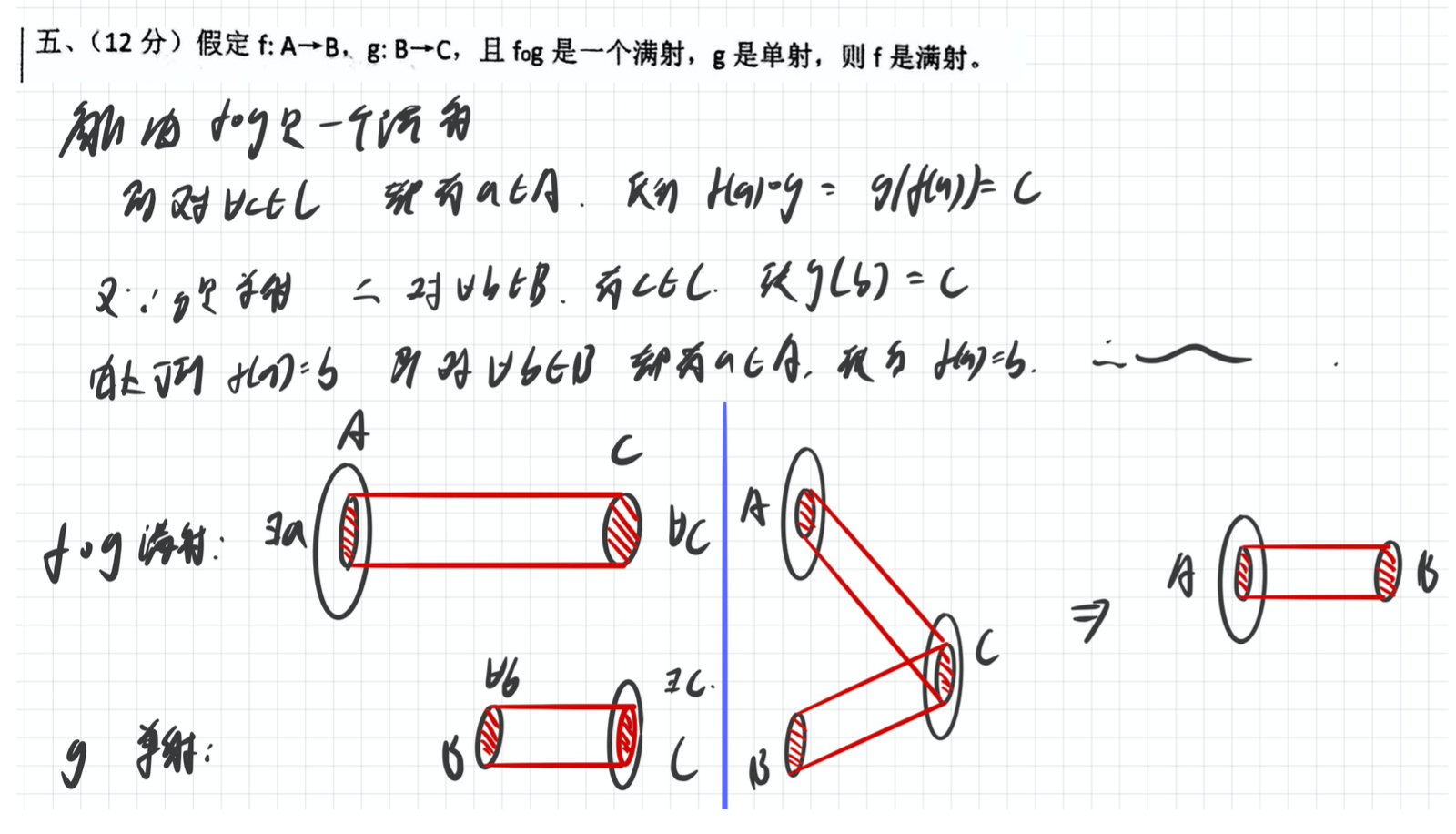
证明单射、满射和双射(单射+满射)
证明单射:证明当x≠y时,f(x)≠f(y),可以取x和x+1等
证明满射:证明对于所有的b∈B,存在a∈A,使得f(a)=b
设R为实数集合,定义f: RXR -> RXR为
f(<x,y>)=<x+2y,x-2y>其中x,y属于R,证明f是双射
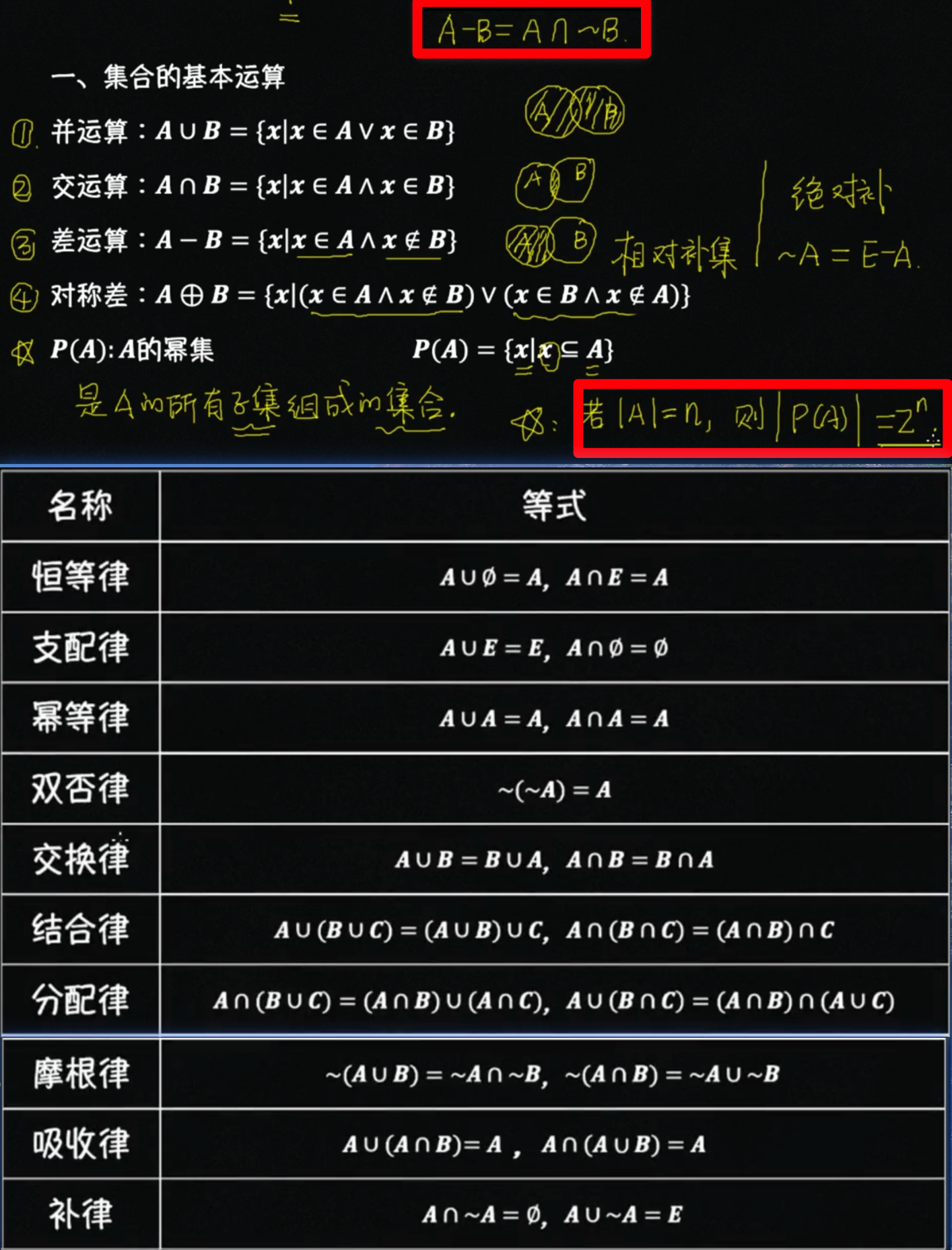
集合
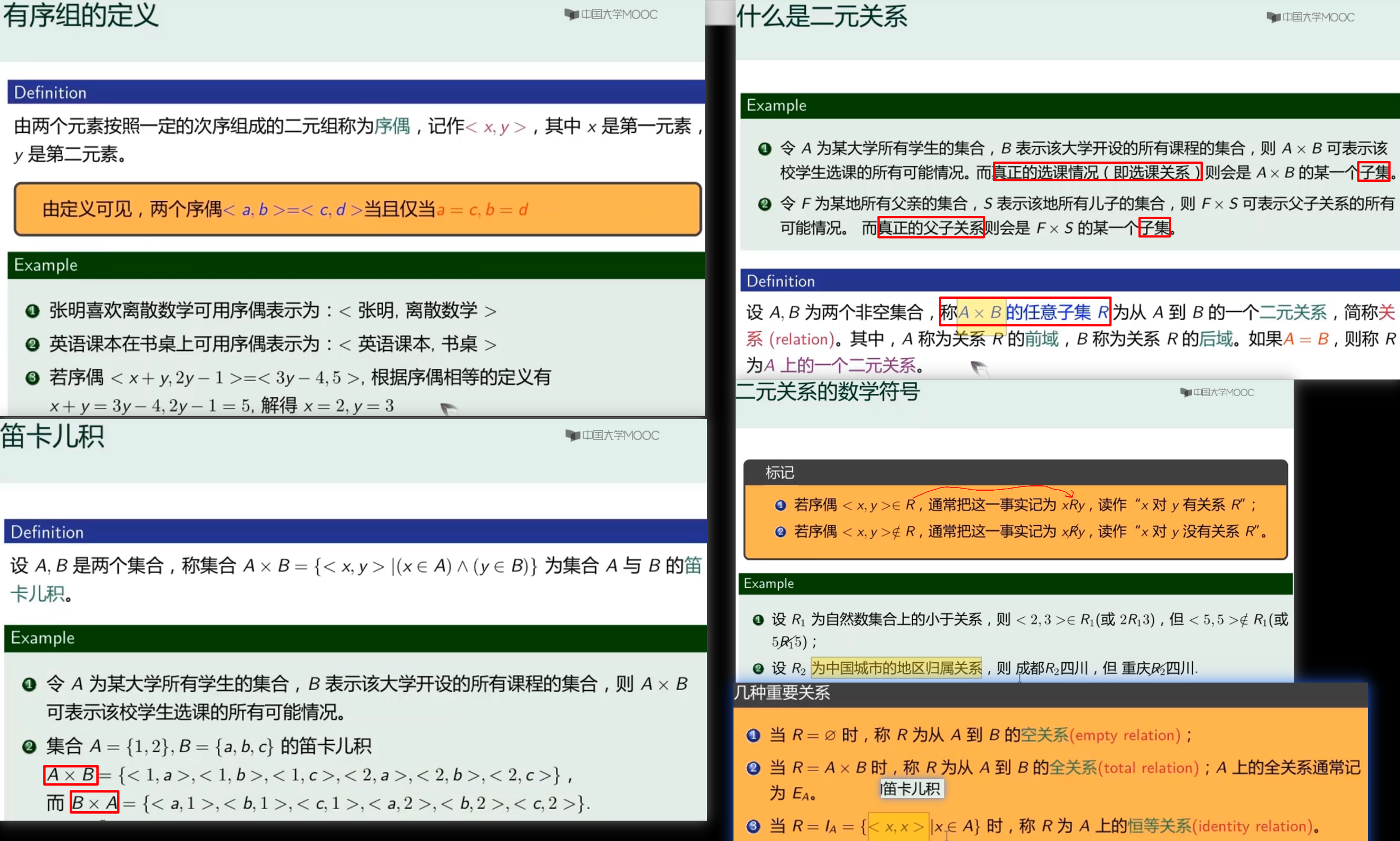
关系
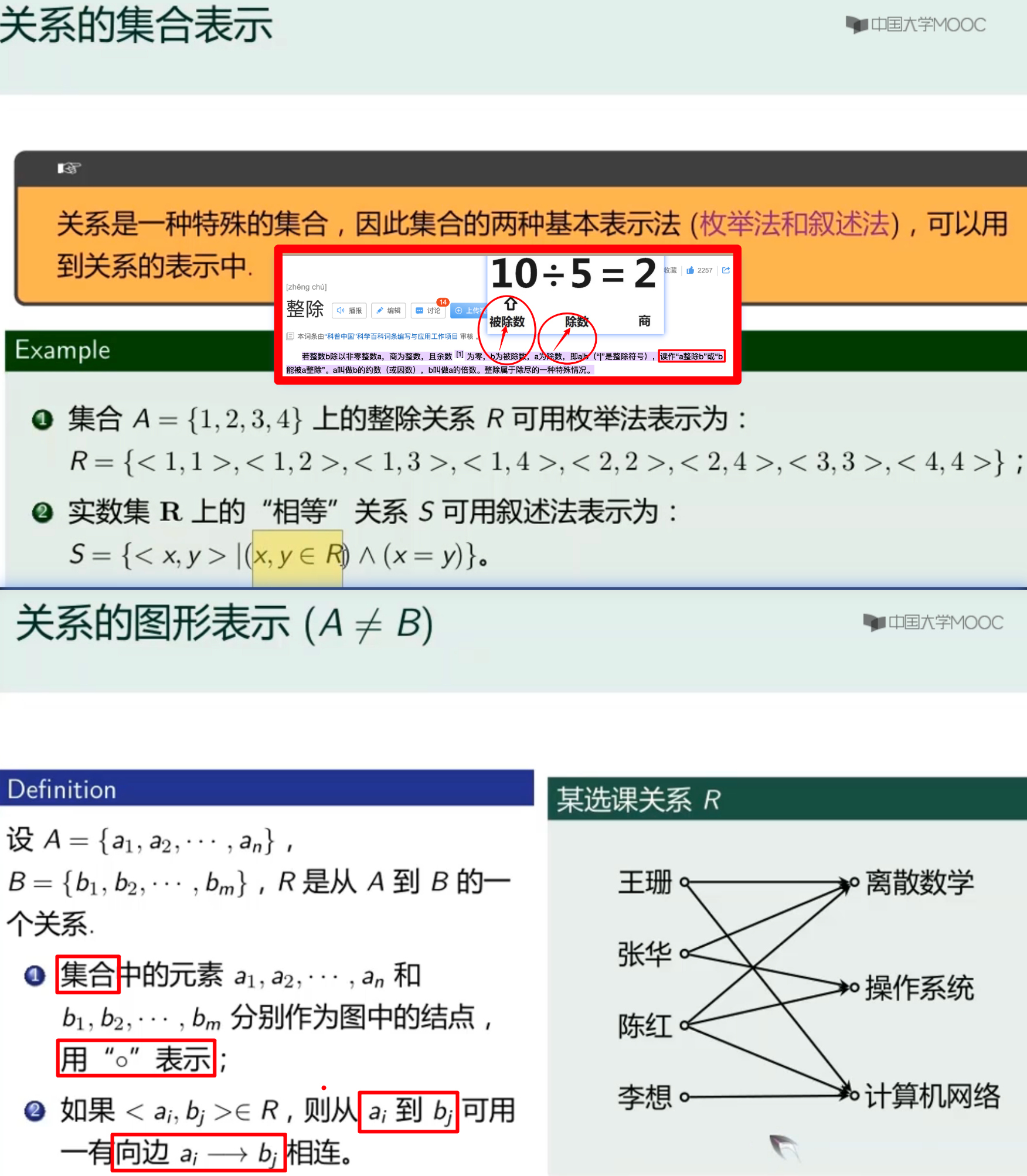
序偶的集合用R
- 有序对(序偶)的集合用R
- 嵌套的二元关系
- 当是一元关系的时候:
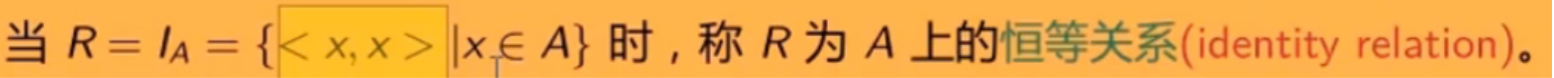
- <<a,b>,<c,d>>这种:

- 嵌套的I为
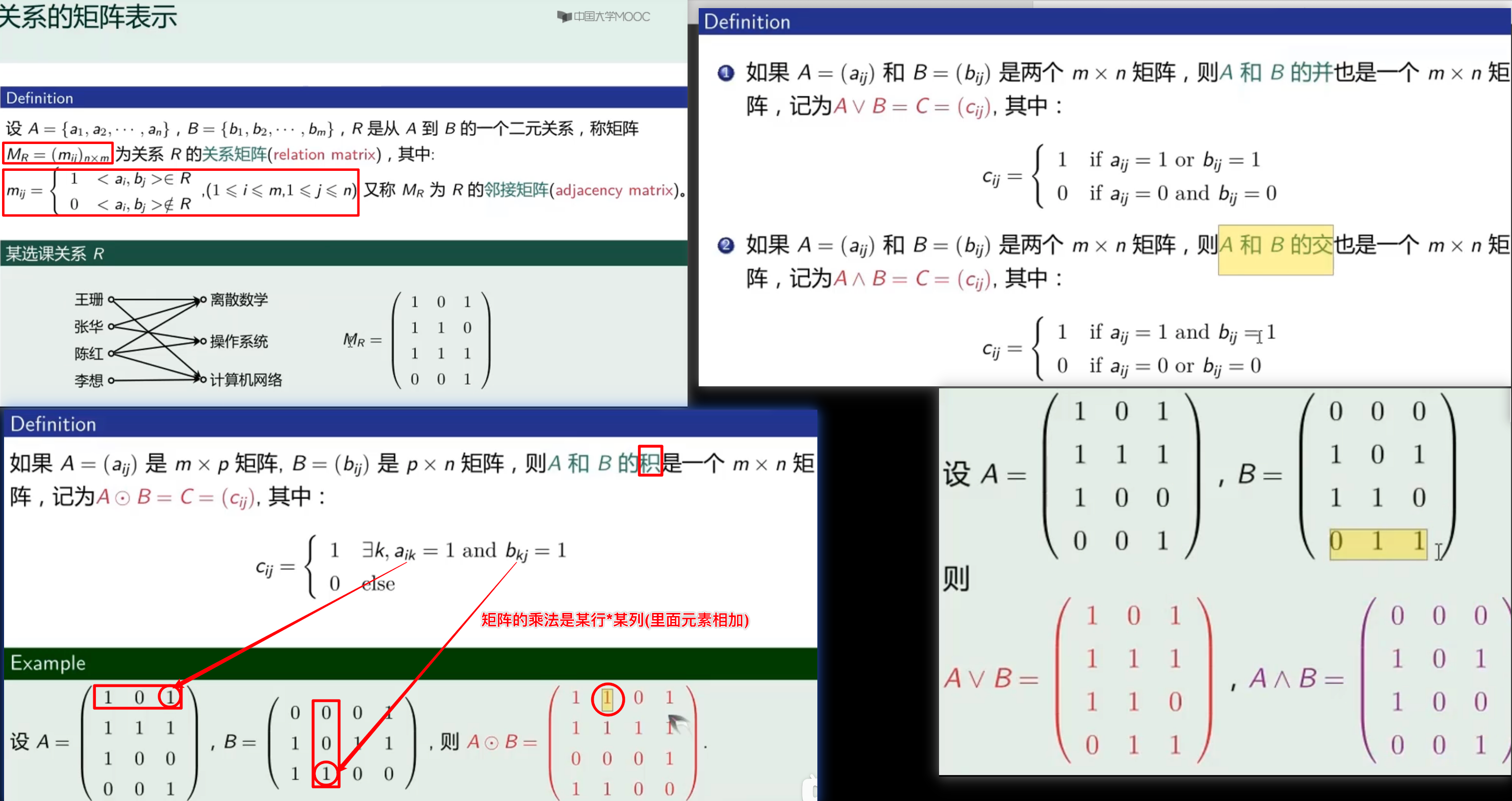
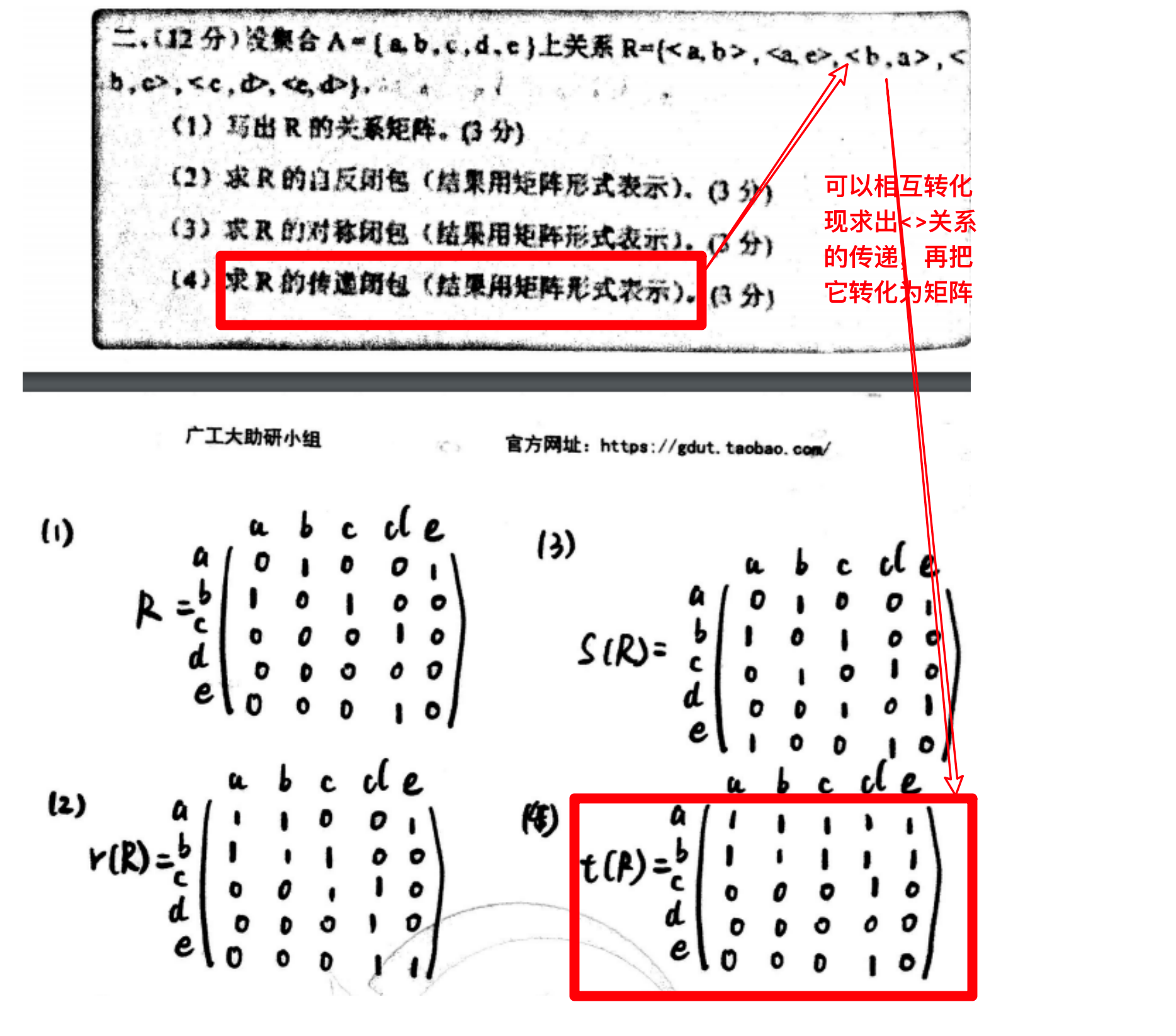
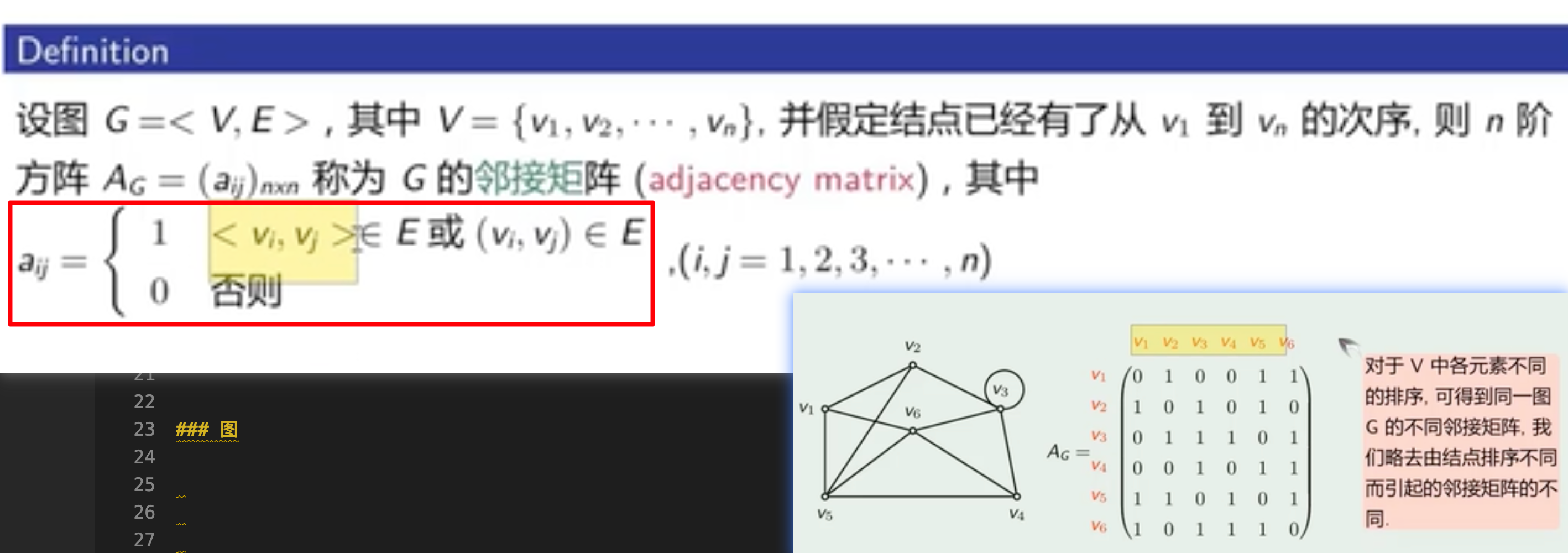
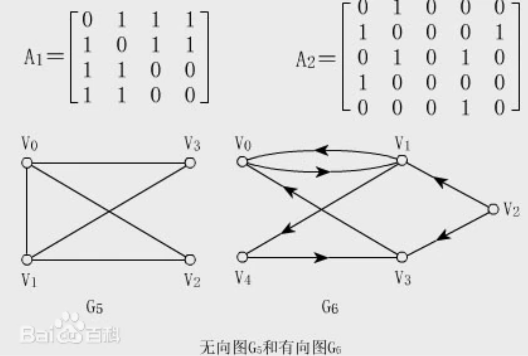
关系图/关系矩阵
- 邻接矩阵用
- 关系图用
五个关系
-
r(R)自反(Reverse): 首先仅有自己,自己反应该结果就是<自己,自己>
-
每个节点都有子环
-
-
s(R)对称(Symmetric): 就不需要管<x,y>;
-
反对称: 就需要对
<x,y>;x==y,这种开恩- 因为它实际上不算是对称,它是自己内部本身就对称
- 任何一对节点之间至多只有一条边
-
t(R)传递(Transfer)
- x到y有一条边,y到z有一条边,那么x到z也会有一条边
运算
- 闭包是只能增加元素对,那么只能是自反,对称,传递
- 反自反: 需要某某不在里面, 那么如果它开始不是反自反(比如是自反,然后需要去掉
<x,y>;x==y)
- 反自反: 需要某某不在里面, 那么如果它开始不是反自反(比如是自反,然后需要去掉
=(等价) <=(偏序) <(拟序)
-
是某某集合上的关系:
-
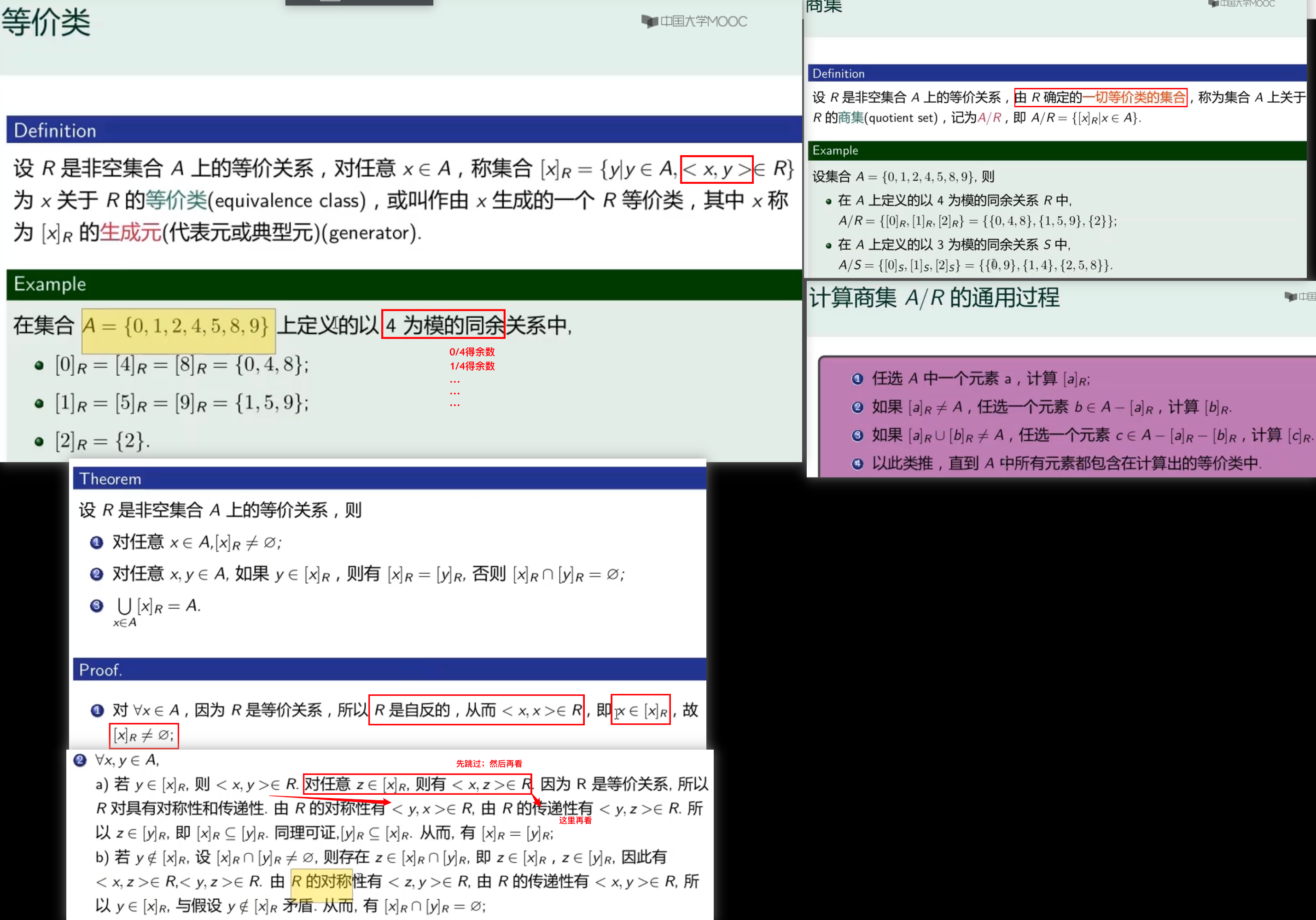
等价关系与偏序关系,只是对称/反对称这一点不一致;
- 偏序了,肯定不是对称了,反对称.
-
偏序关系(局部序关系partial order)-全序关系:
- 集合A包含B则称A大于B,显然存在两个集合互相不包含,那么这两个集合就没发比大小
- 全序关系就是偏序关系,只不过它
- 偏序关系就是指存在“序”这个概念,满足自反性、反对称性和传递性。但是并不是任何两个元素之间都有这个序的先后关系。比如集合之间的包含关系,就是一个偏序关系。但并不是任何两个集合之间都存在包含关系。
- 感谢这个答案,我从本科就没办法根据教科室和老师的解释深入理解“偏序”这个概念。遇到它,我要么忘记它的涵义,要么还得看定义再次理解。看了你的回答后我马上就明白了,”局部“这个解释才是对的,最“数学”的解释,肯定忘不了(数学上不就用partial表示“局部”的意思吗)。“偏序”这个中文翻译有问题,要是我就翻译成“局部序”,简单直接明了,而且数学上经常讲"局部",并不会讲"偏颇、偏心"。“偏”字跟“局部”毫无关系。第一个用“partial order"这个词的外国人,肯定是取"partial"这个字的"局部的"这个意思吧,取个"偏心的,不公平的"就没了数学上的意义。母语英语的一看”partial order“即便不懂也明白大概,母语汉语的一看”偏序“就懵逼(我实在是没有办法让它跟”偏“联系起来)。
-
良序集-全序集
- 良序集 [2] 是任意非空子集都有最小元的全序集。
-
偏序关系: <=关系.
-
拟序关系: 实数集上的小于关系是拟序关系.
<
-
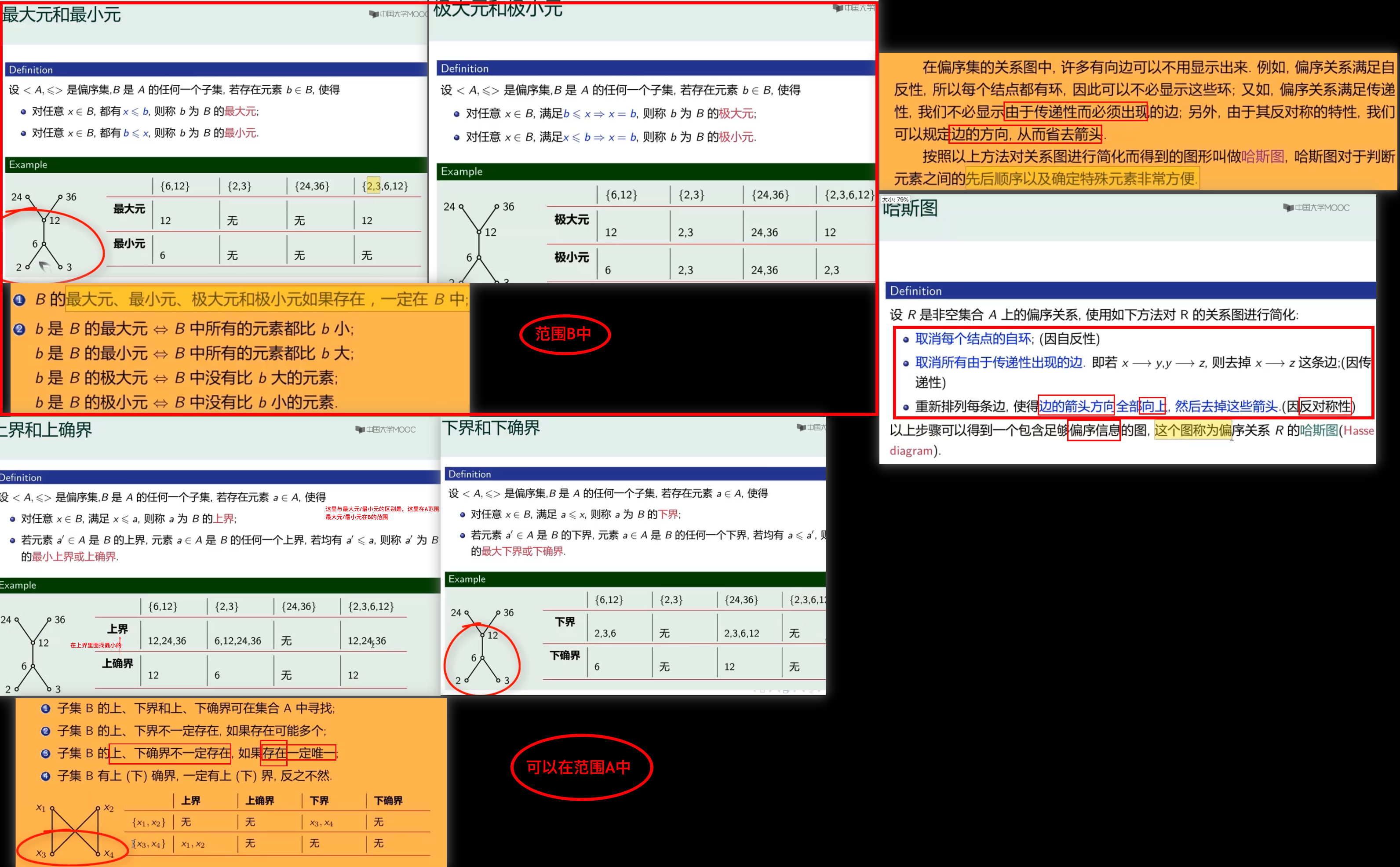
最大/小;极大/小;上/下界;确界;都为
-
最大元: 比任何其他元素都
-
极大元: 如果b小于等于某个元素,那么这个元素一定是它自己
-
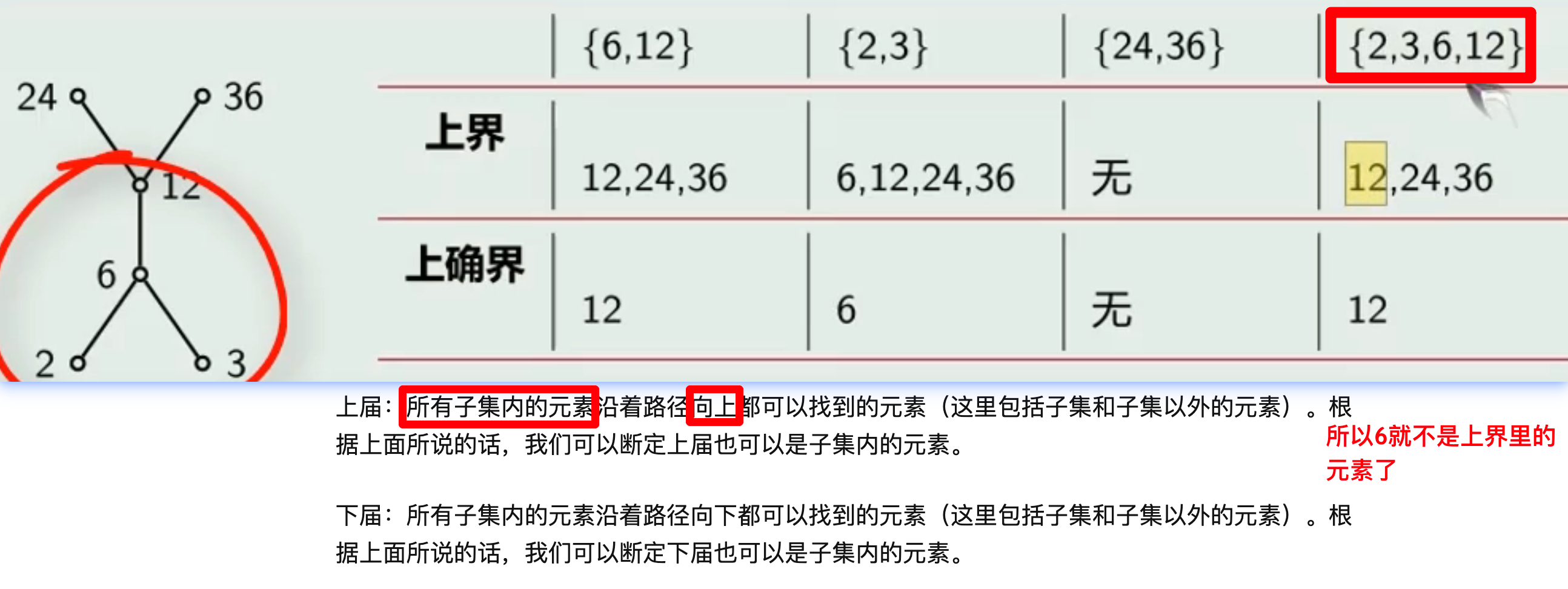
上下确界:上界里面取最小,下界里面取最大
哈斯图: 1>求出所有相关的集合(不包括中的) 2>去掉所有的传递 3>
- 偏序关系: 这个东东 自反/反对称/传递
- 去掉环
- 去掉传递的
一些用词
- 树用T
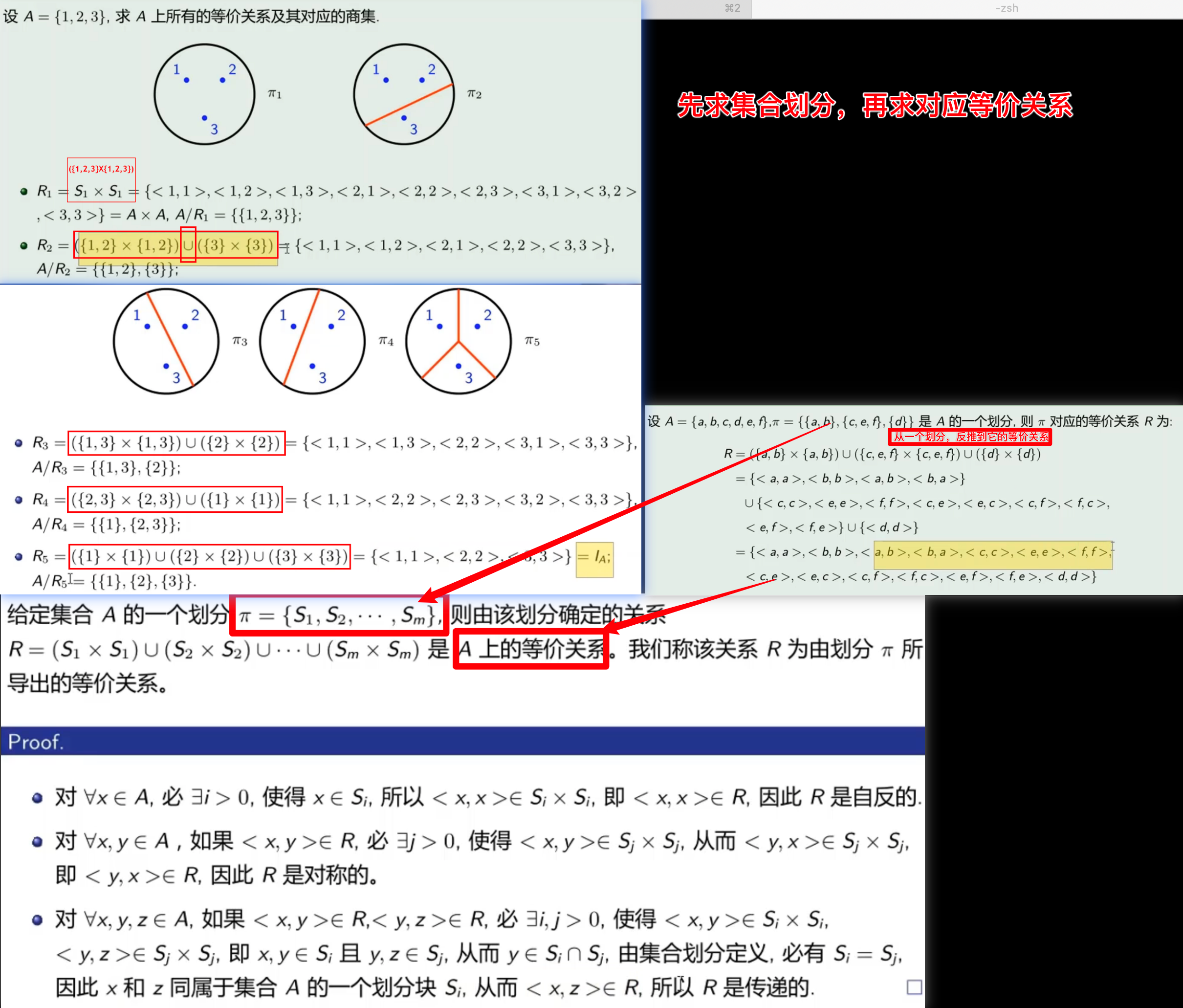
- 划分用
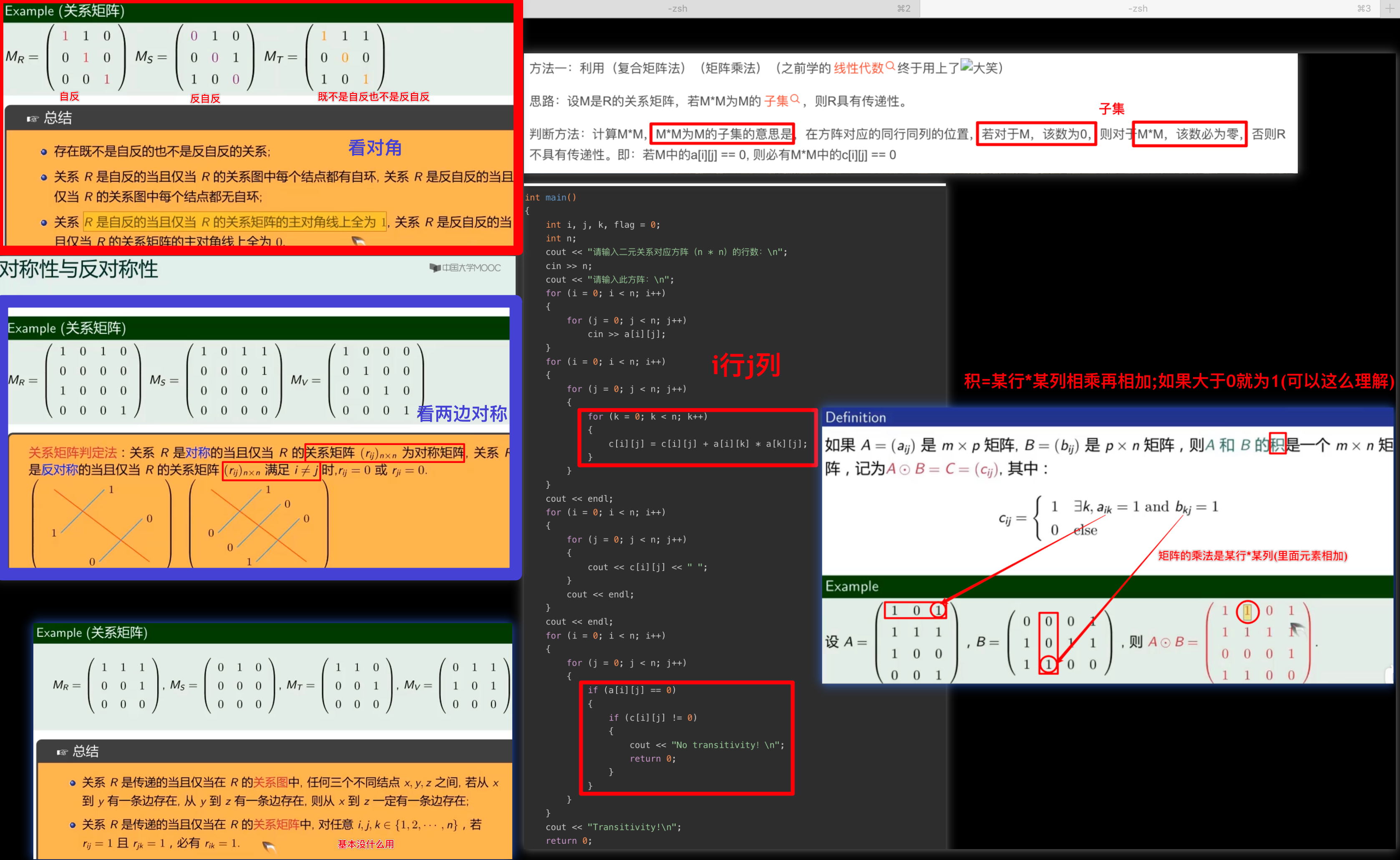
- 二次方的邻接矩阵
- 等于的偏序关系
- 入度deg+(vi)
- 集合的矩阵和图的矩阵不一样 !!!
- 图的矩阵不一定只是 1 !!!
题型
关系矩阵判断自反/对称/传递
最大/小元-极大/小元-上/下界
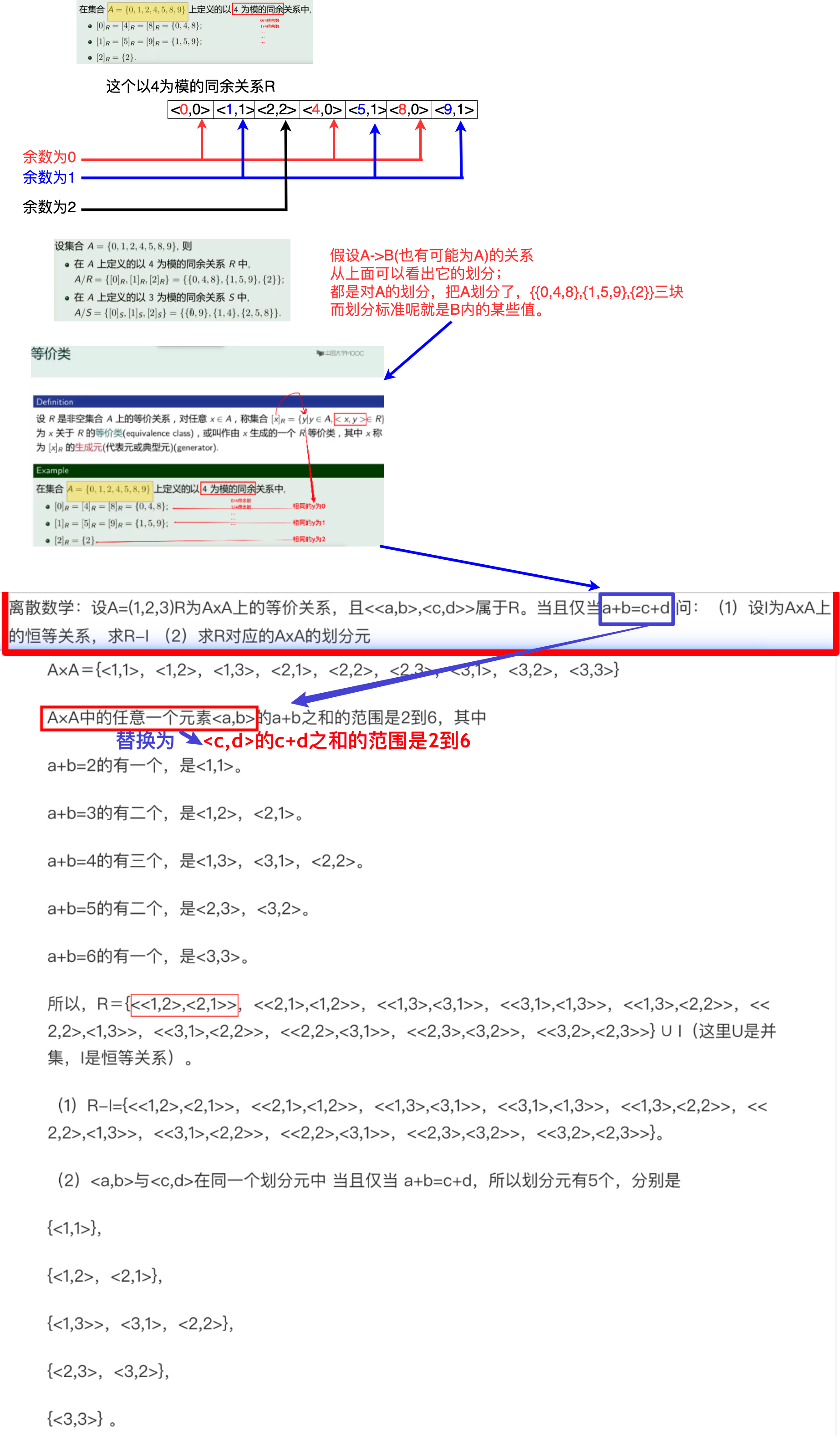
求集合的划分
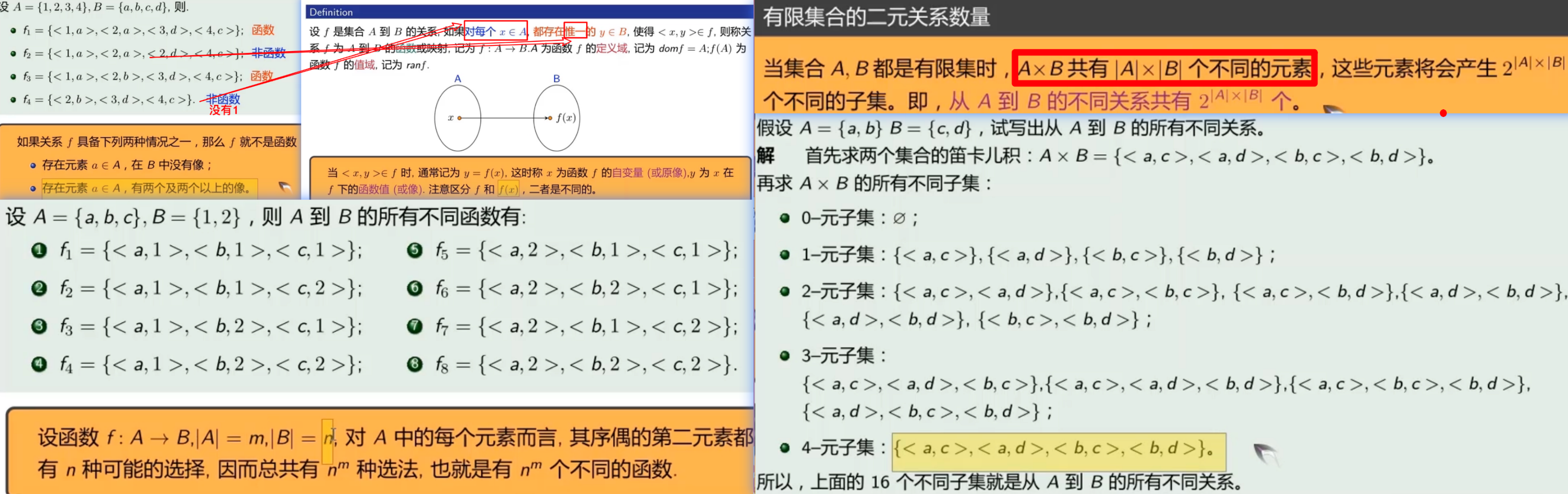
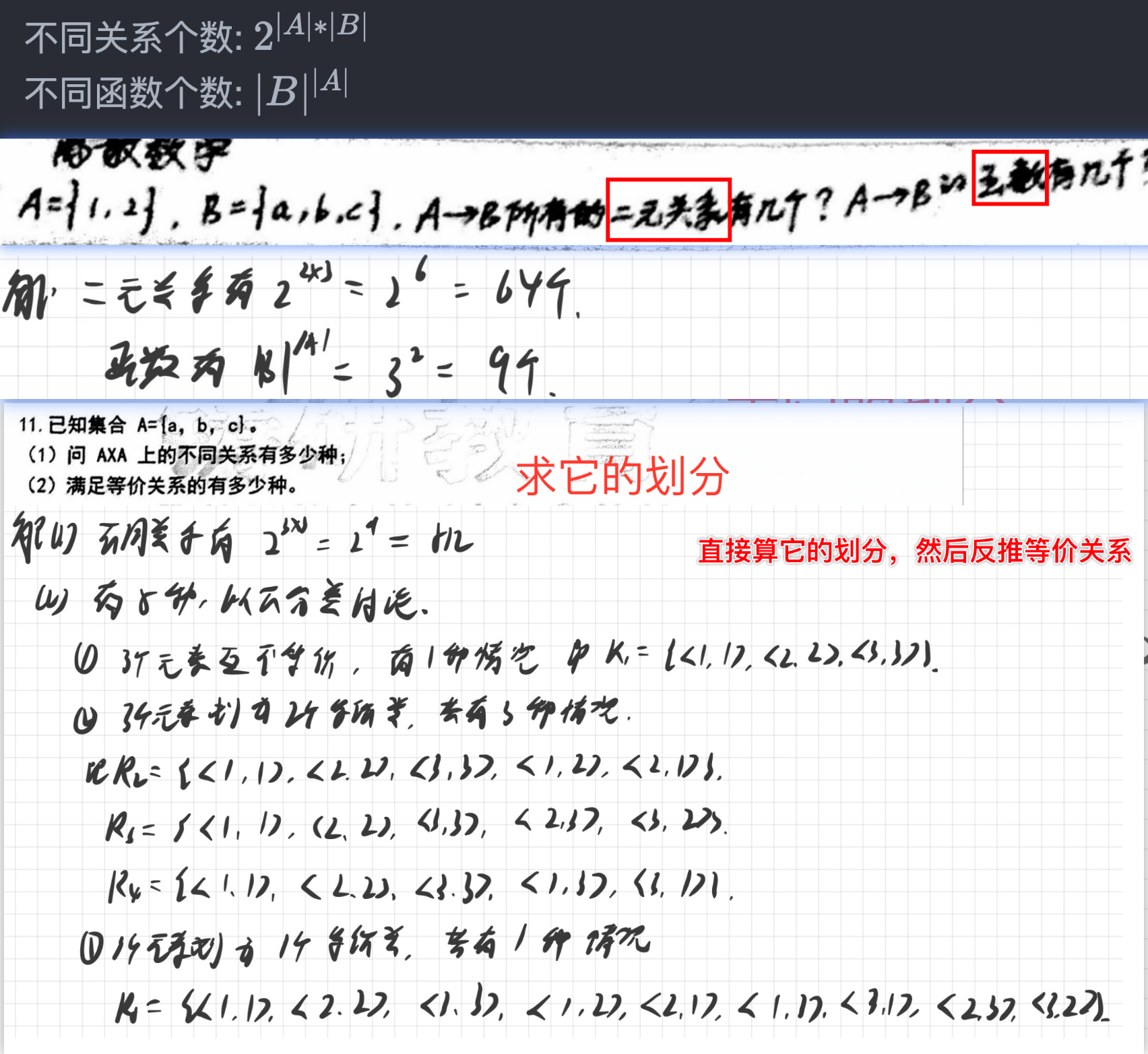
不同关系个数:
不同函数个数:
求关系R在A到B(可能为A)划分块
图
-
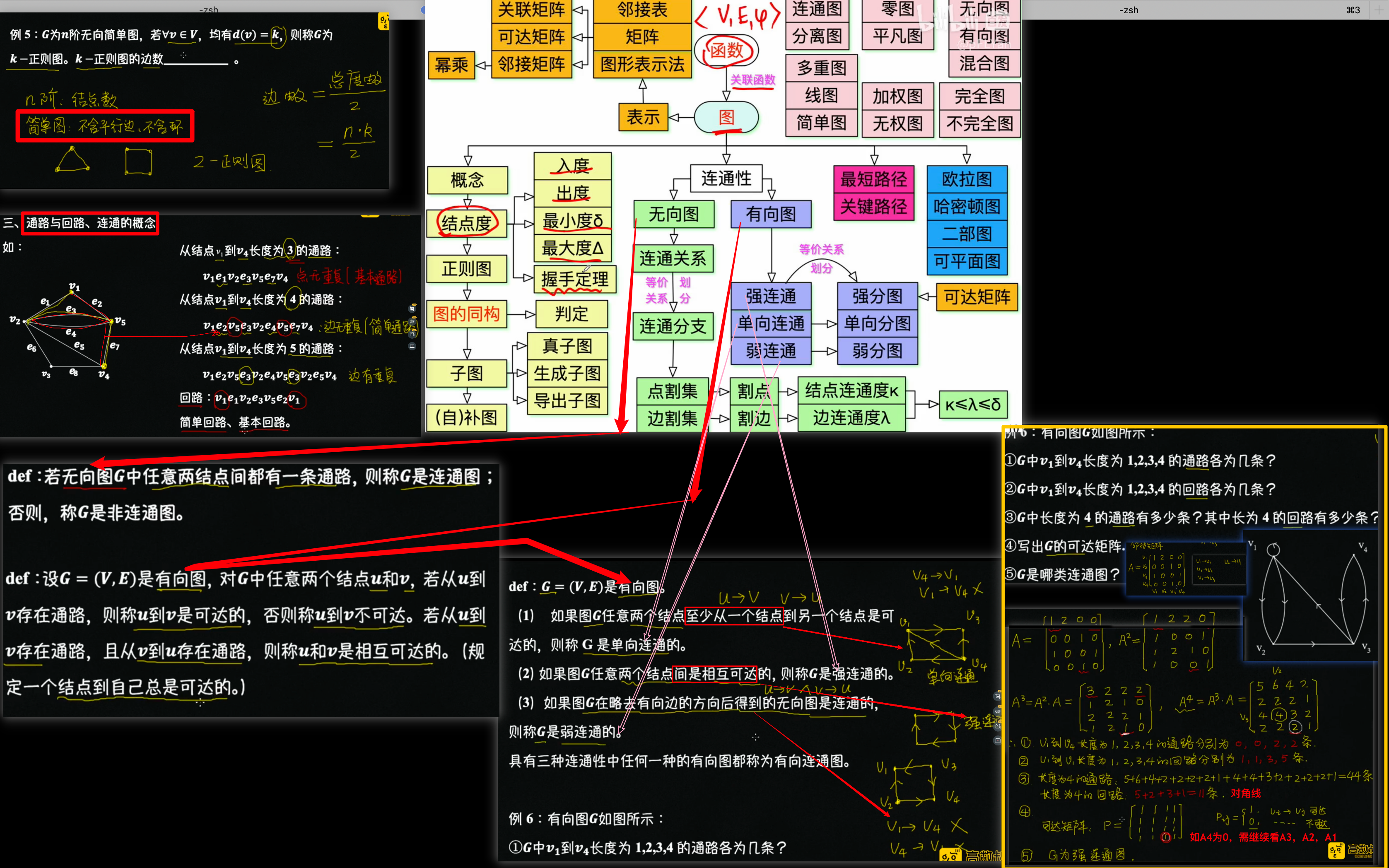
-
按连通性分类:
-
按平行边分类:
- 平行边:
- 在有向图中,两结点间 (包括结点自身间) 若有同始点和同终点的几条边,则这几条边 称为平行边;
- 在无向图中,两结点间 (包括结点自身间) 若有几条边,则这几条边称 为平行边。
- 两结点 a 、 b 间相互平行的边的条数称为边 (a, b) 或 <a, b> 的重数。
- 含有平行边的图称为多重图(multigraph);
- (不含有平行边的图)非多重图称为线图(line graph);
- 无环的线图称为。
- 平行边:
- 握手定理: 总度数=2m
- 树: m=(n-1)
总度数=2 * (结点数 - 1)
- 平面图:面的次数=2*m
- ⚠️:桥,它的面次数为2
图的表示方法
矩阵
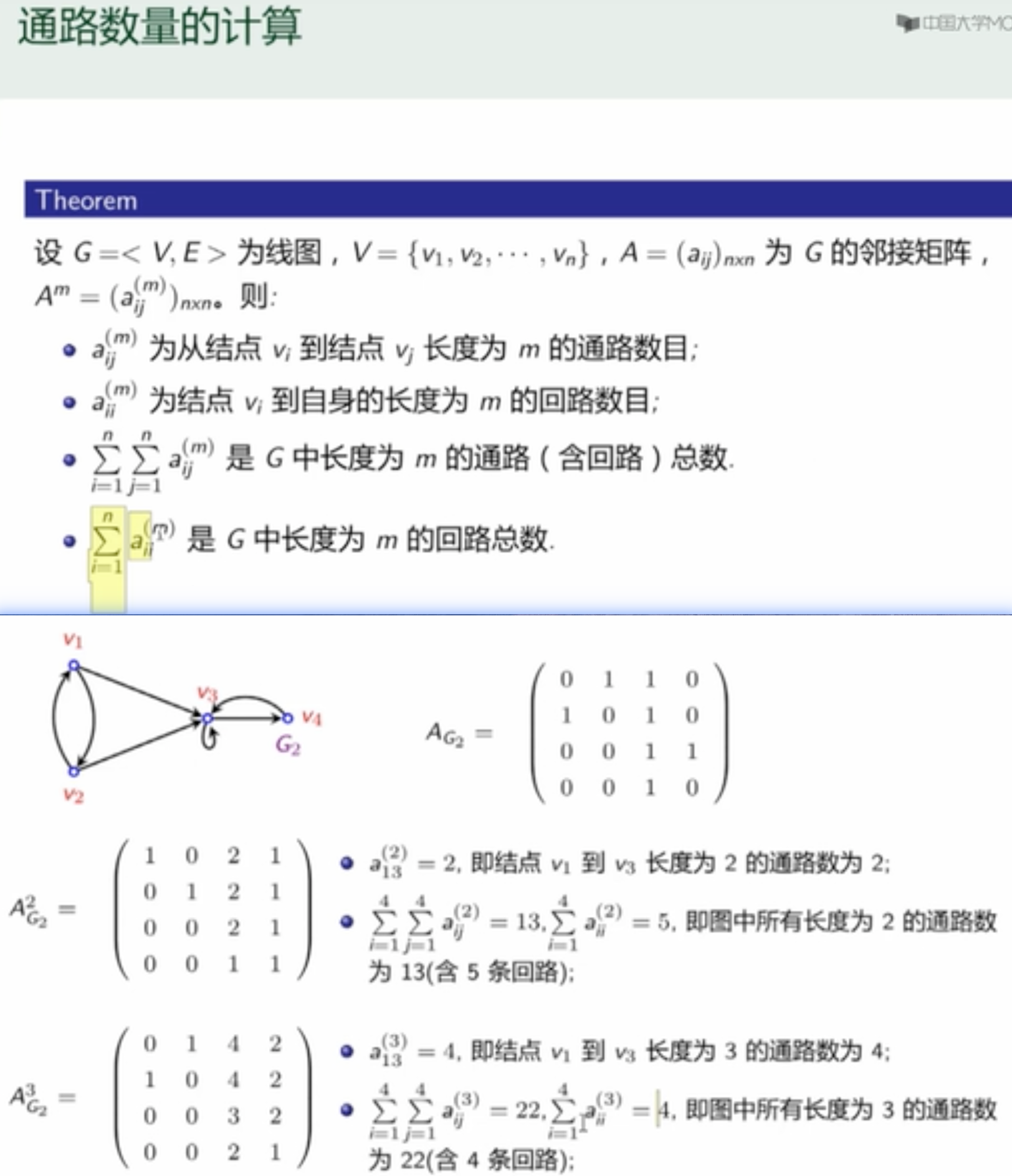
如果是求通路/回路的个数,那么矩阵里面应该是边数目。
如果是求可达->区分是强连通/弱连通/单连通:
- 那么就使用邻接矩阵
邻接点-邻接边
图的分类
-
多重图->线图->简单图:
-
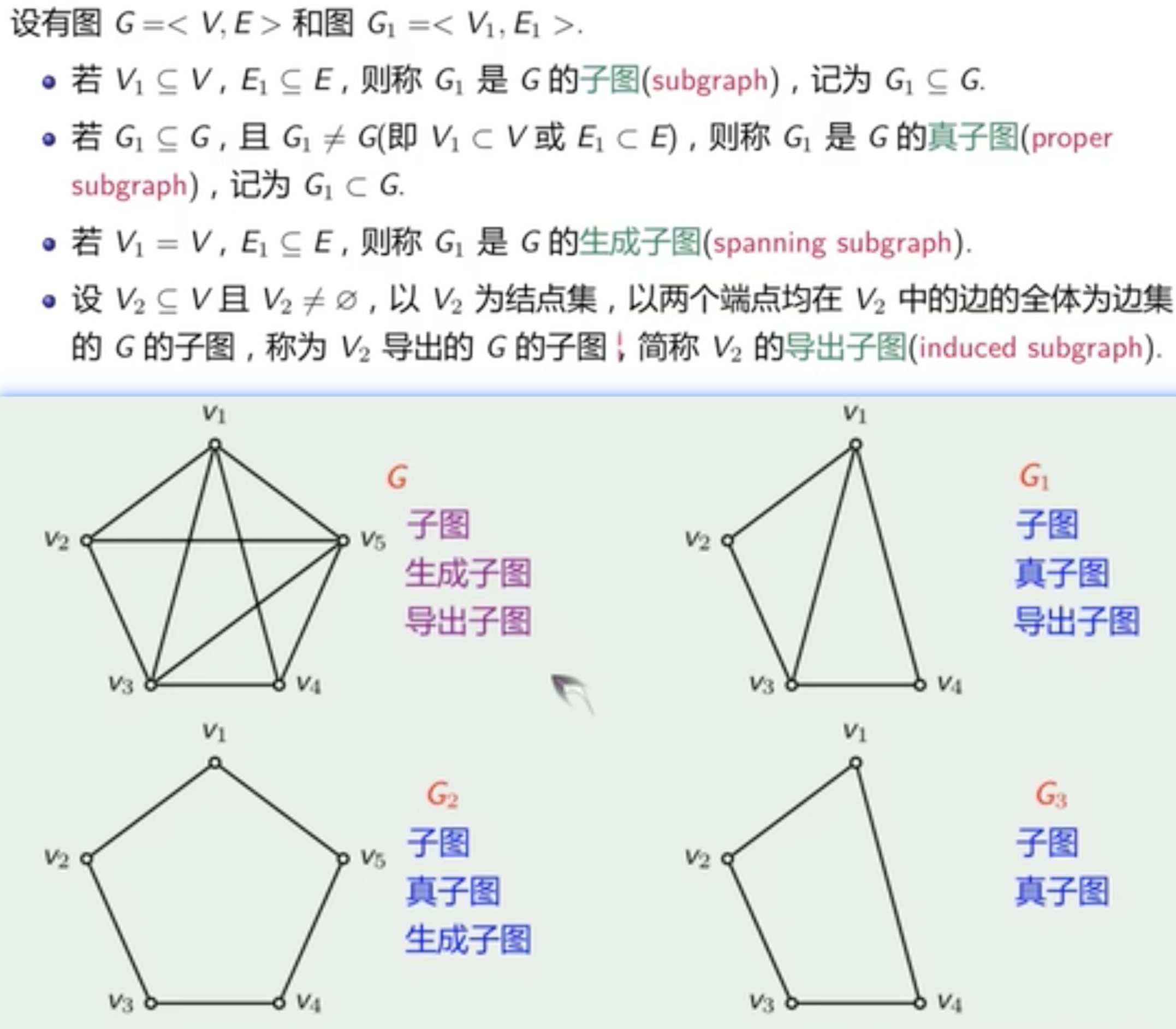
子图
-
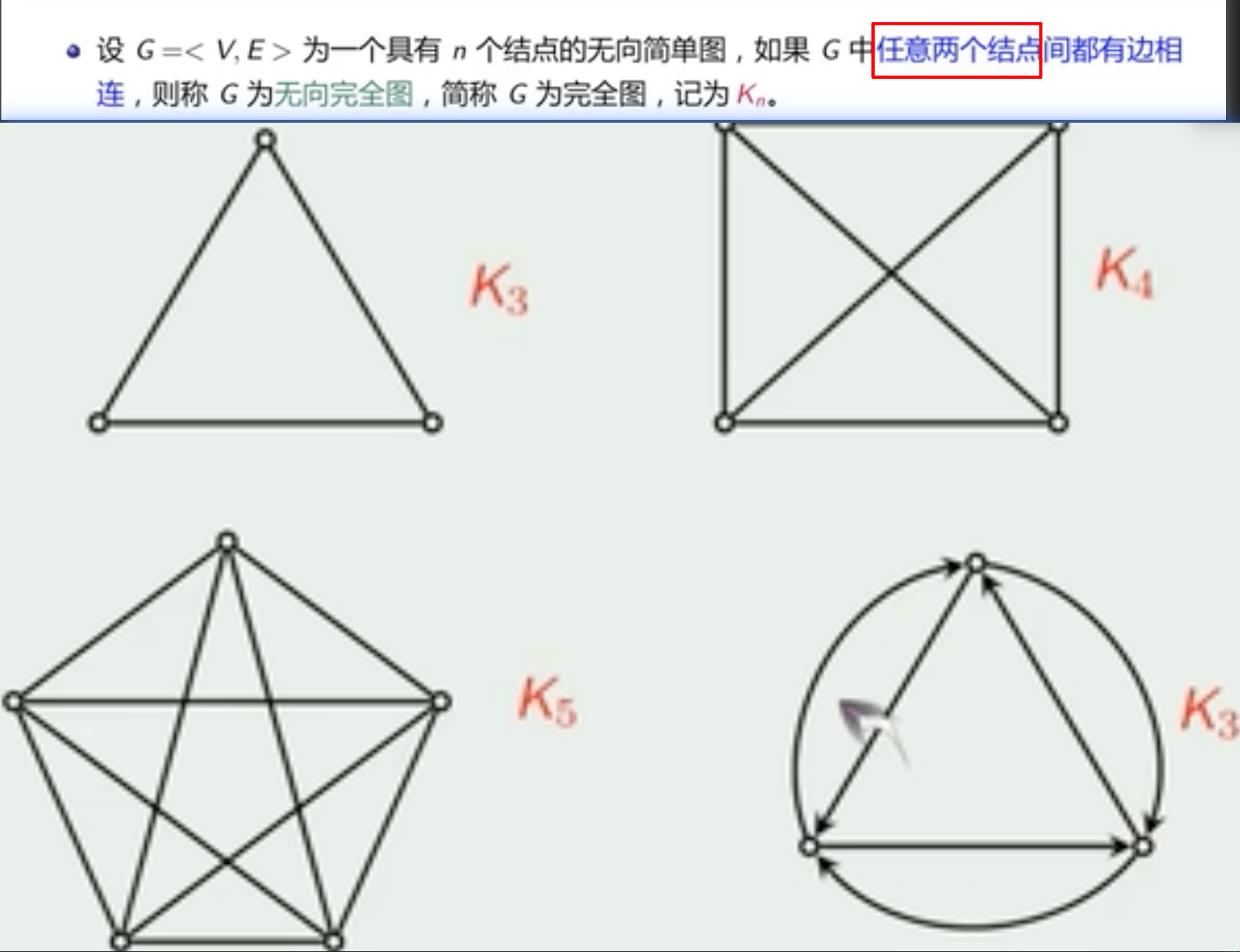
完全图
-
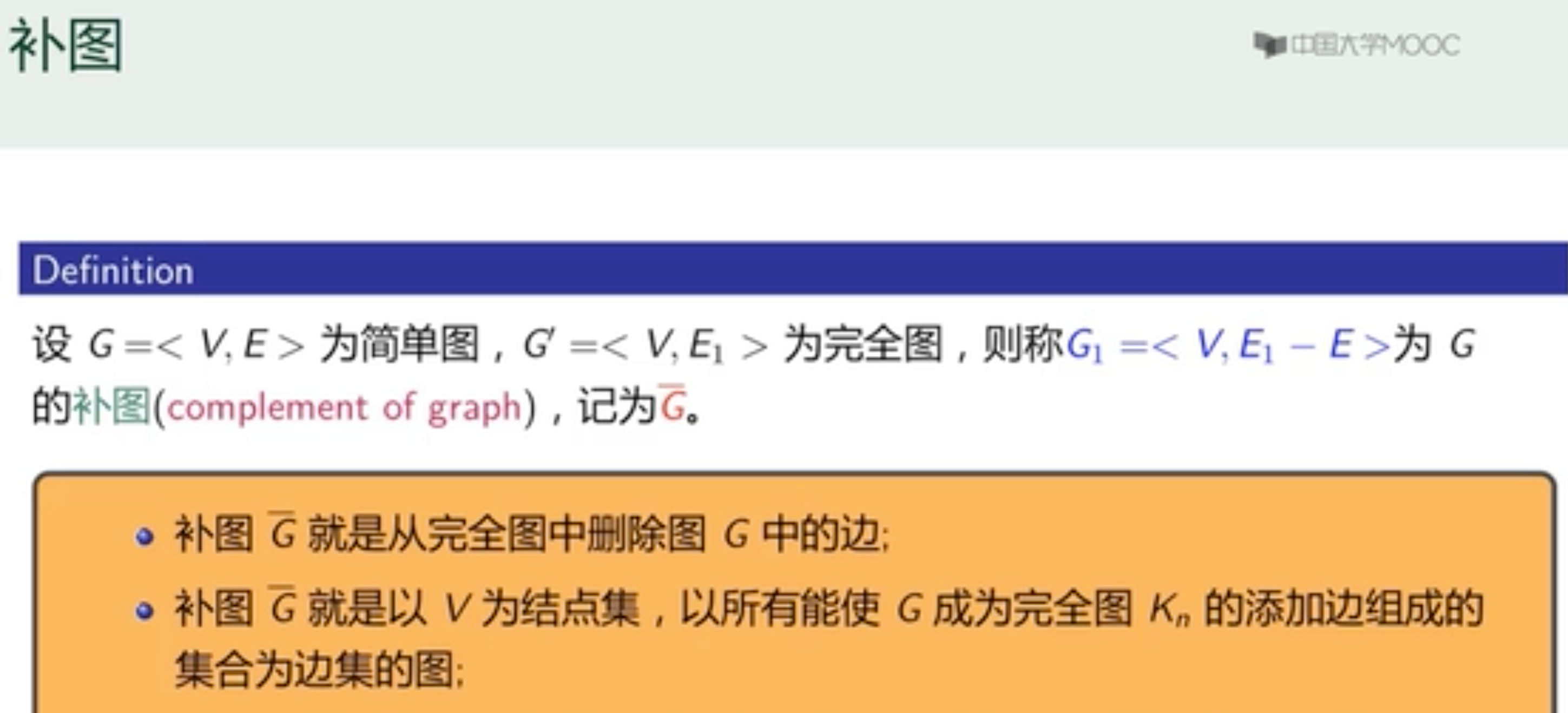
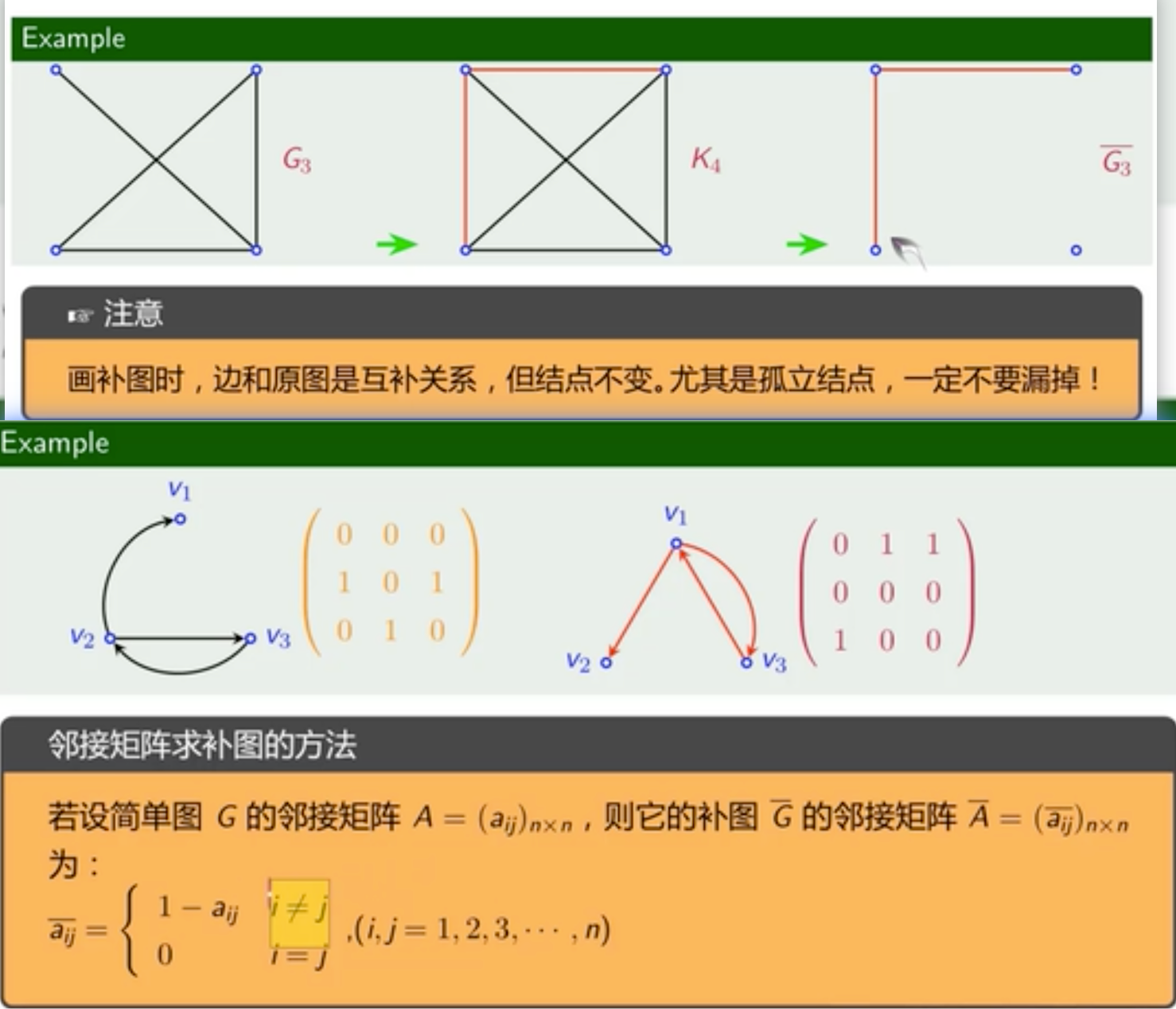
补图
度
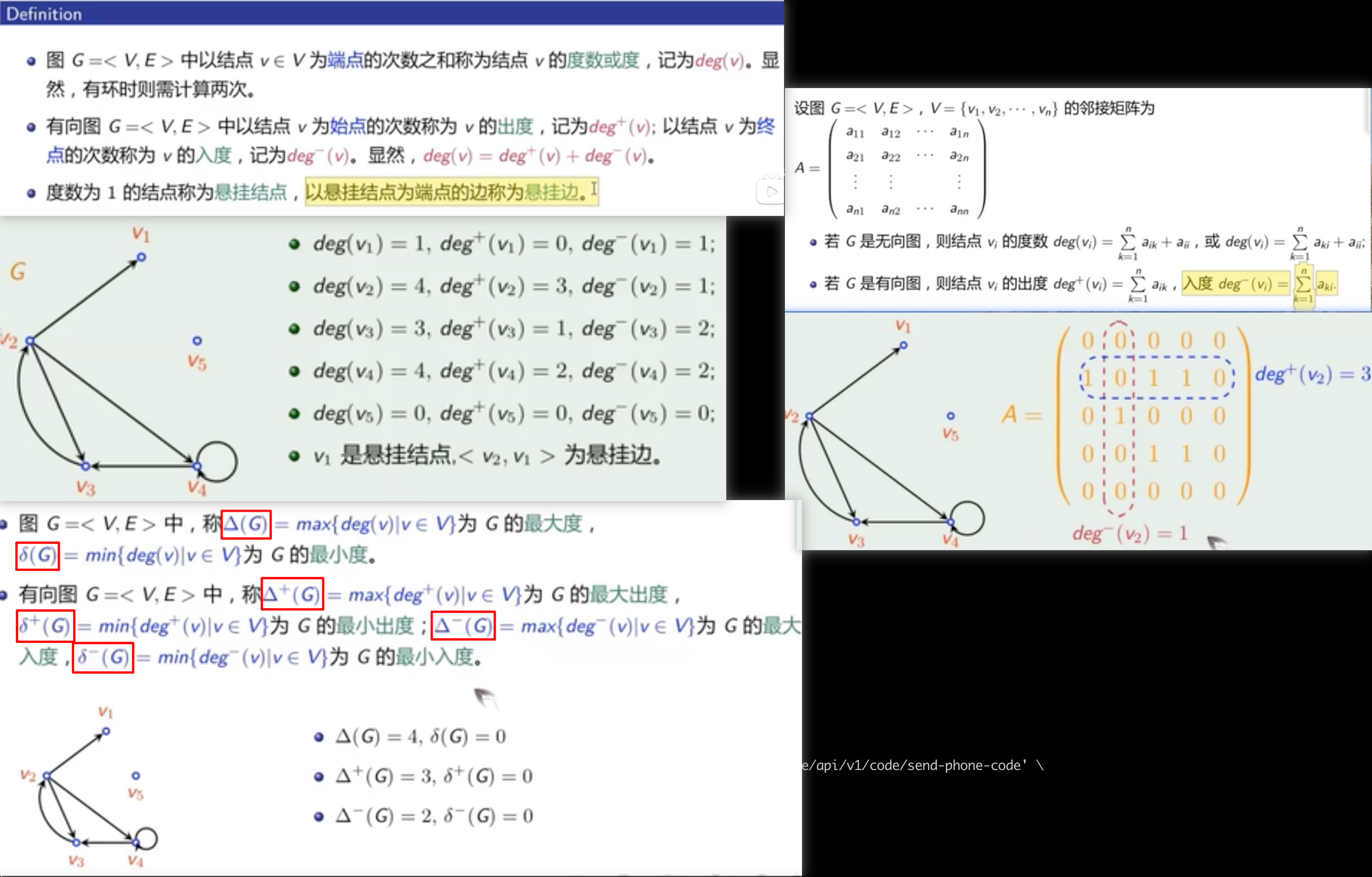
- 握手定理
- 同构
- 握手定理
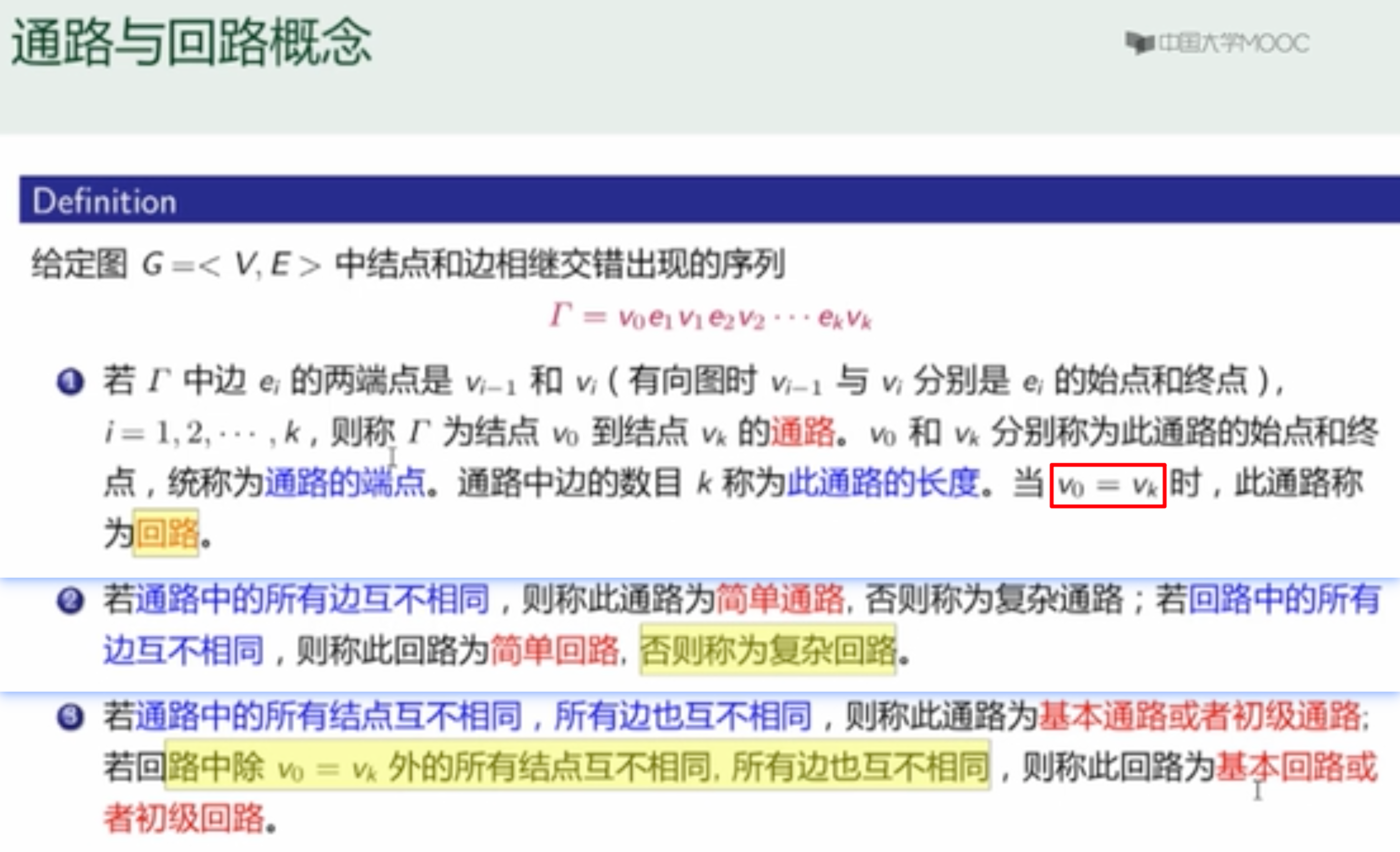
通路/回路
-
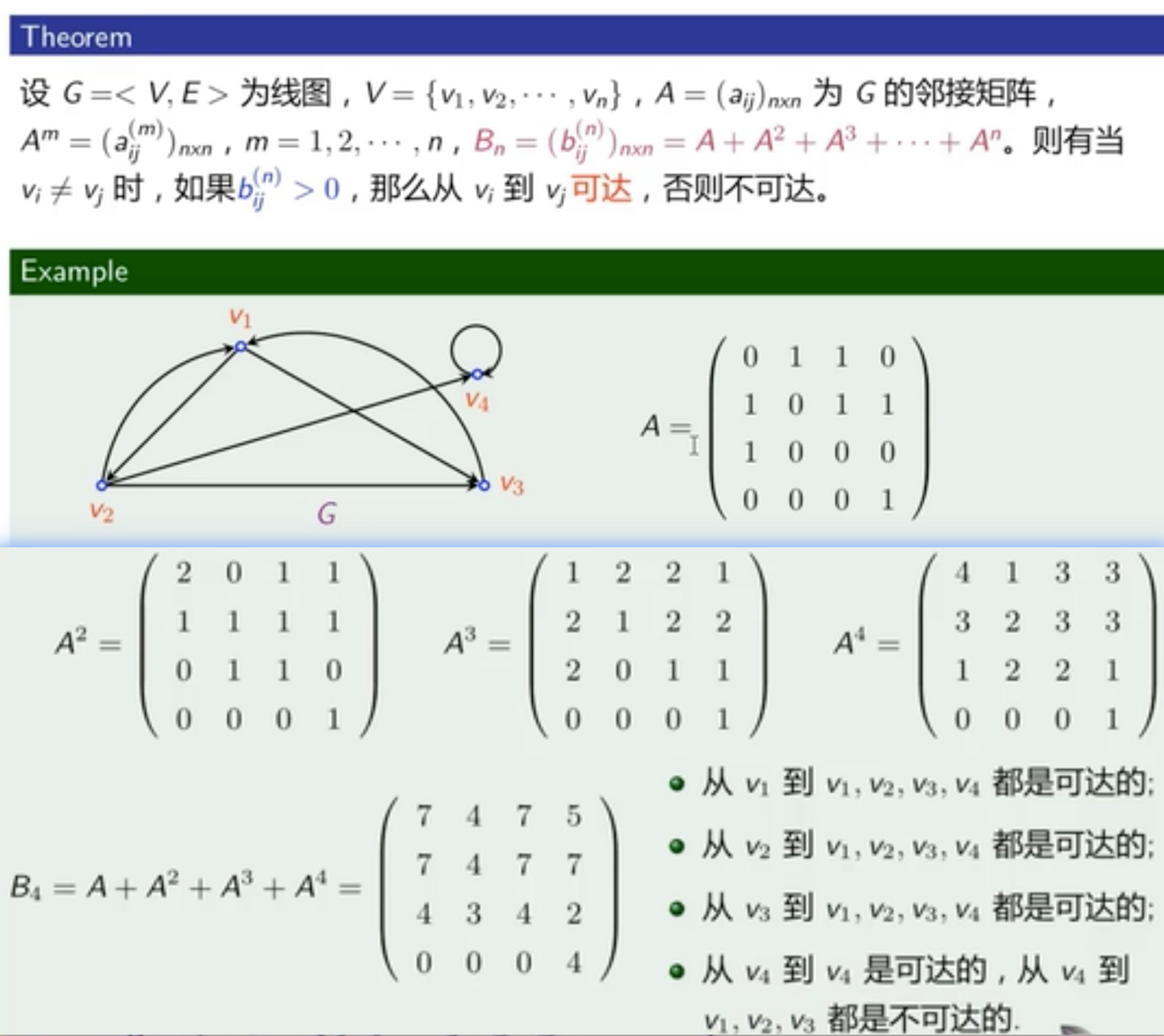
是否可达:

-
- 回路要回到原点,所以它的长度要加一个一。
-
-
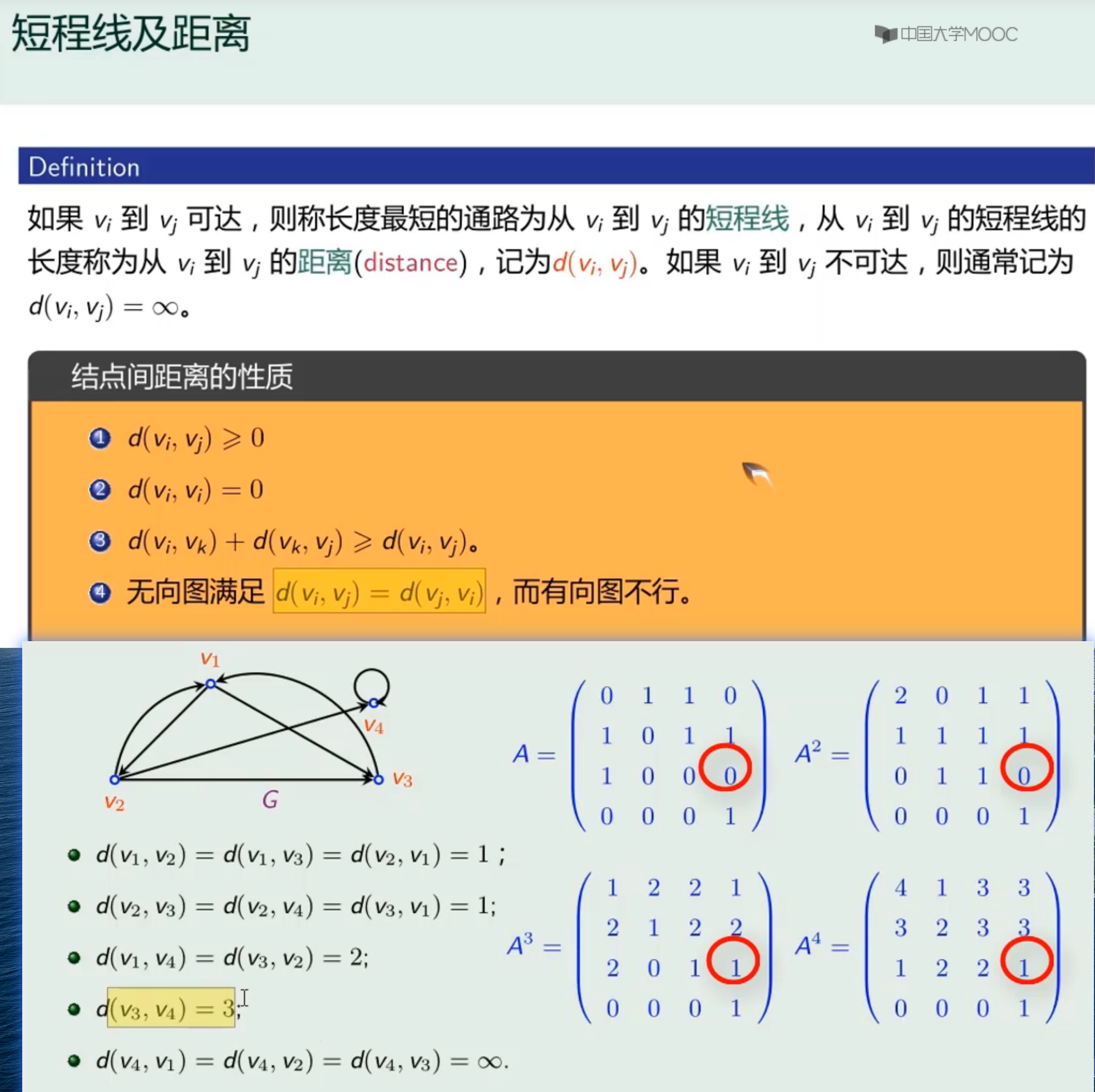
短程线和距离
-
-
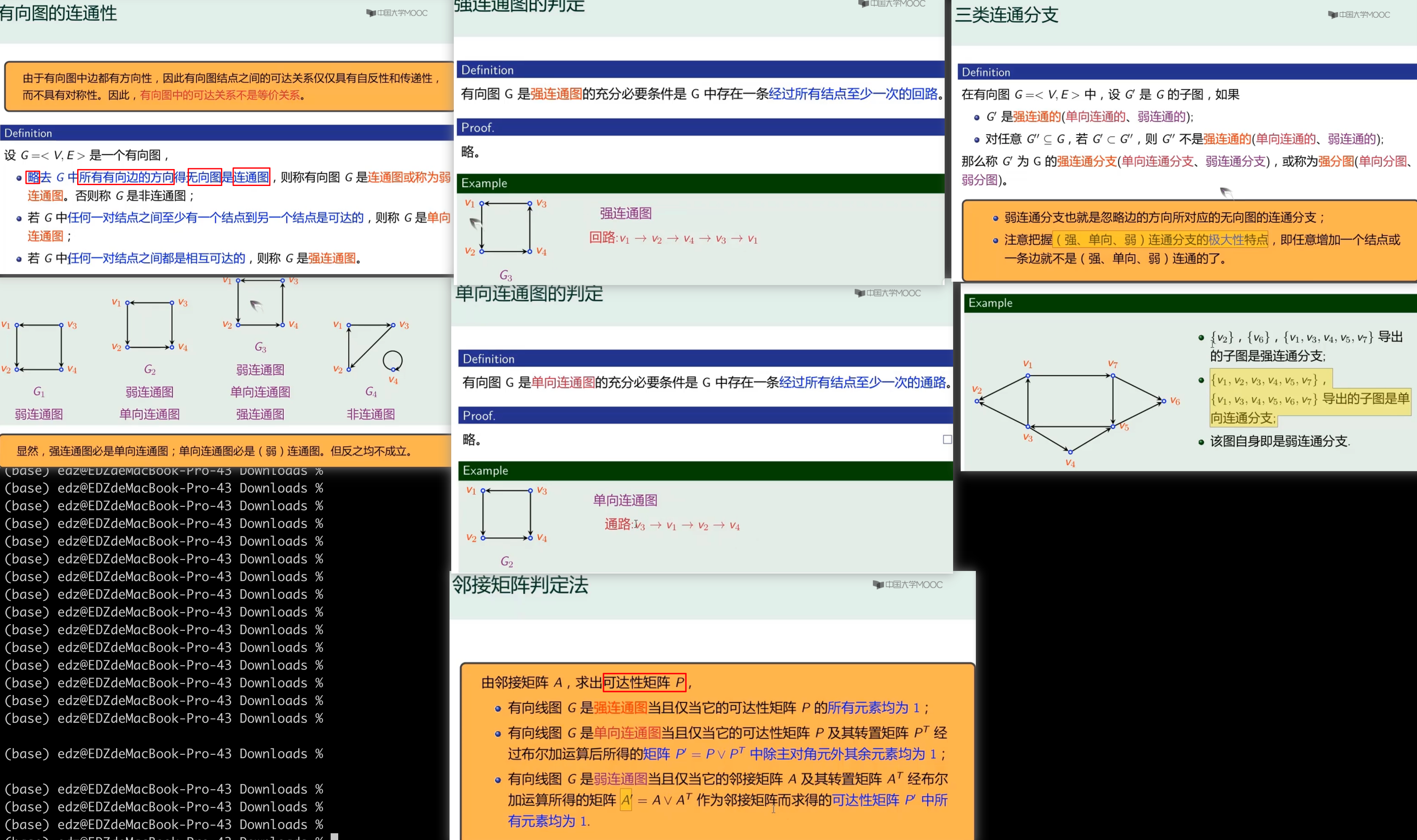
有向图的连通性
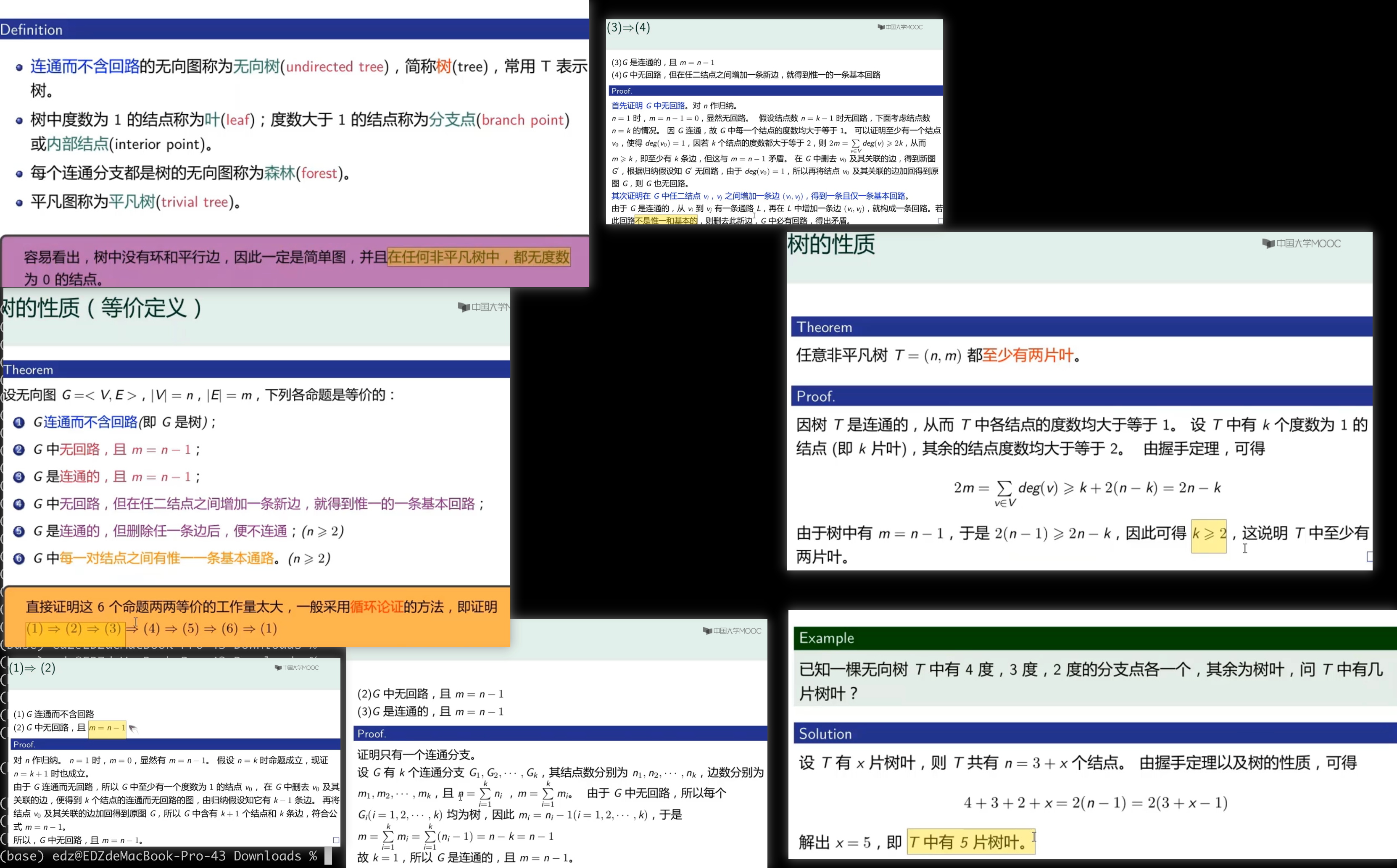
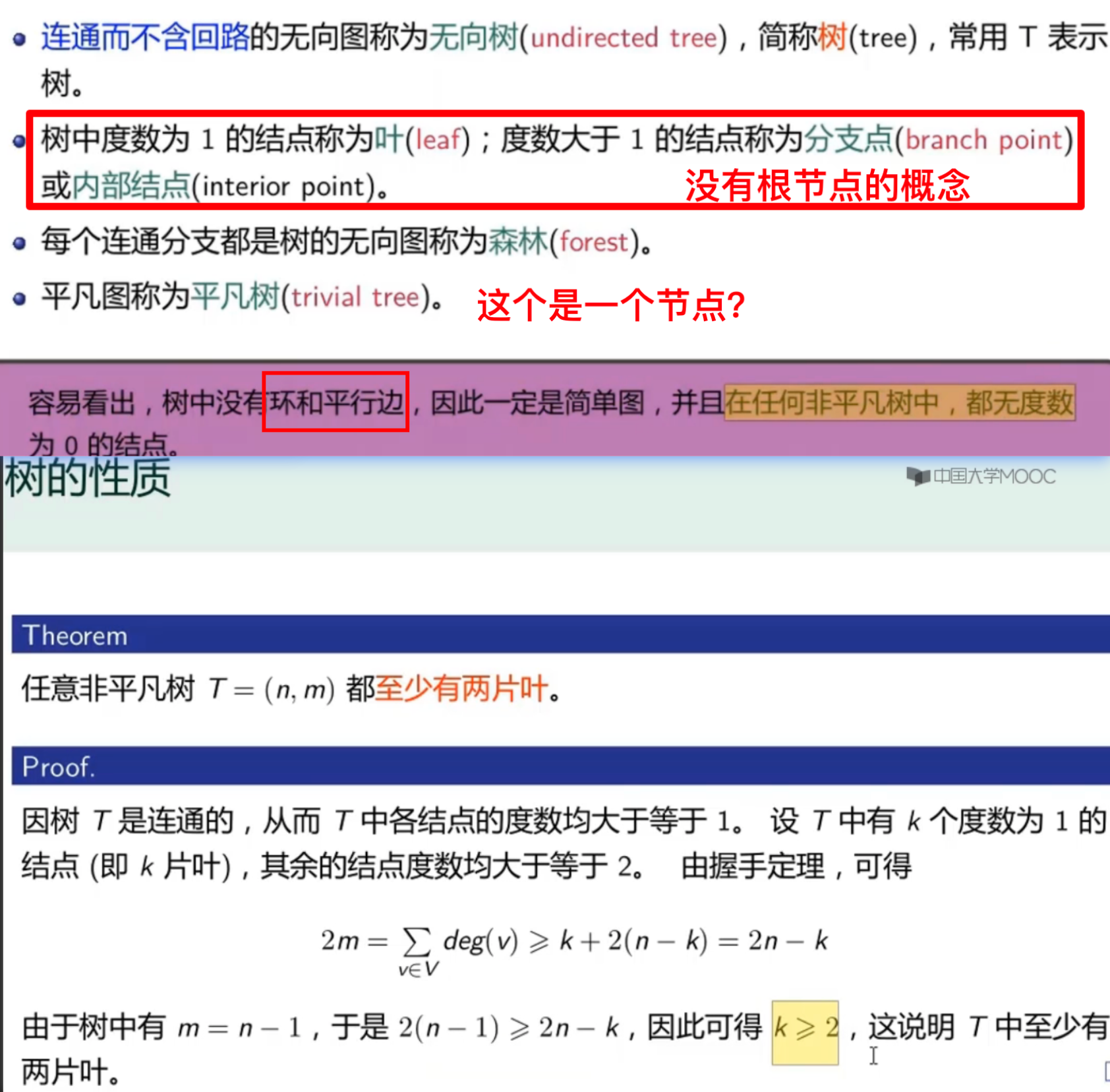
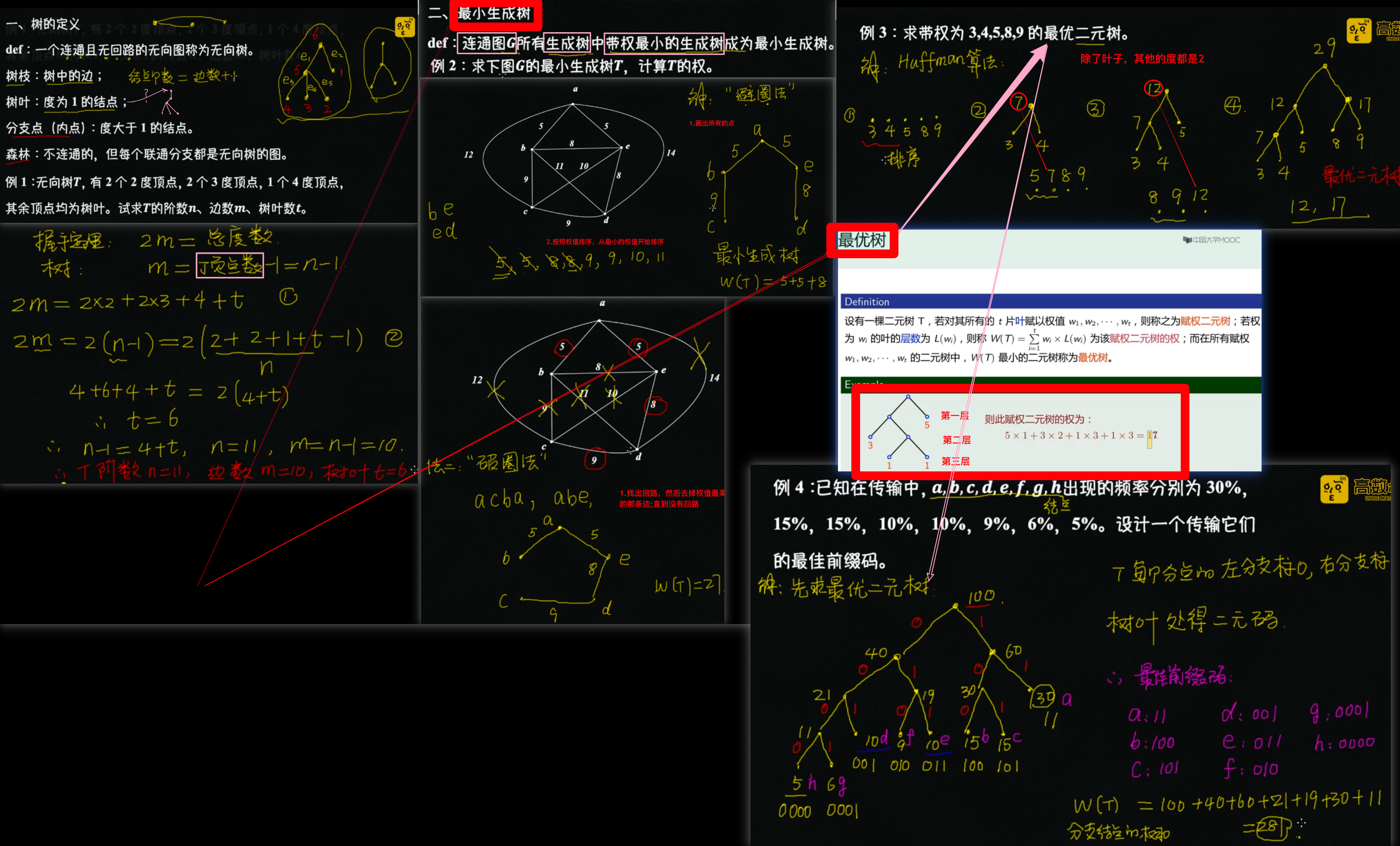
连通而不含回路图(无向树)(简称)
-
-
树的性质
-
生成树存在条件/算法
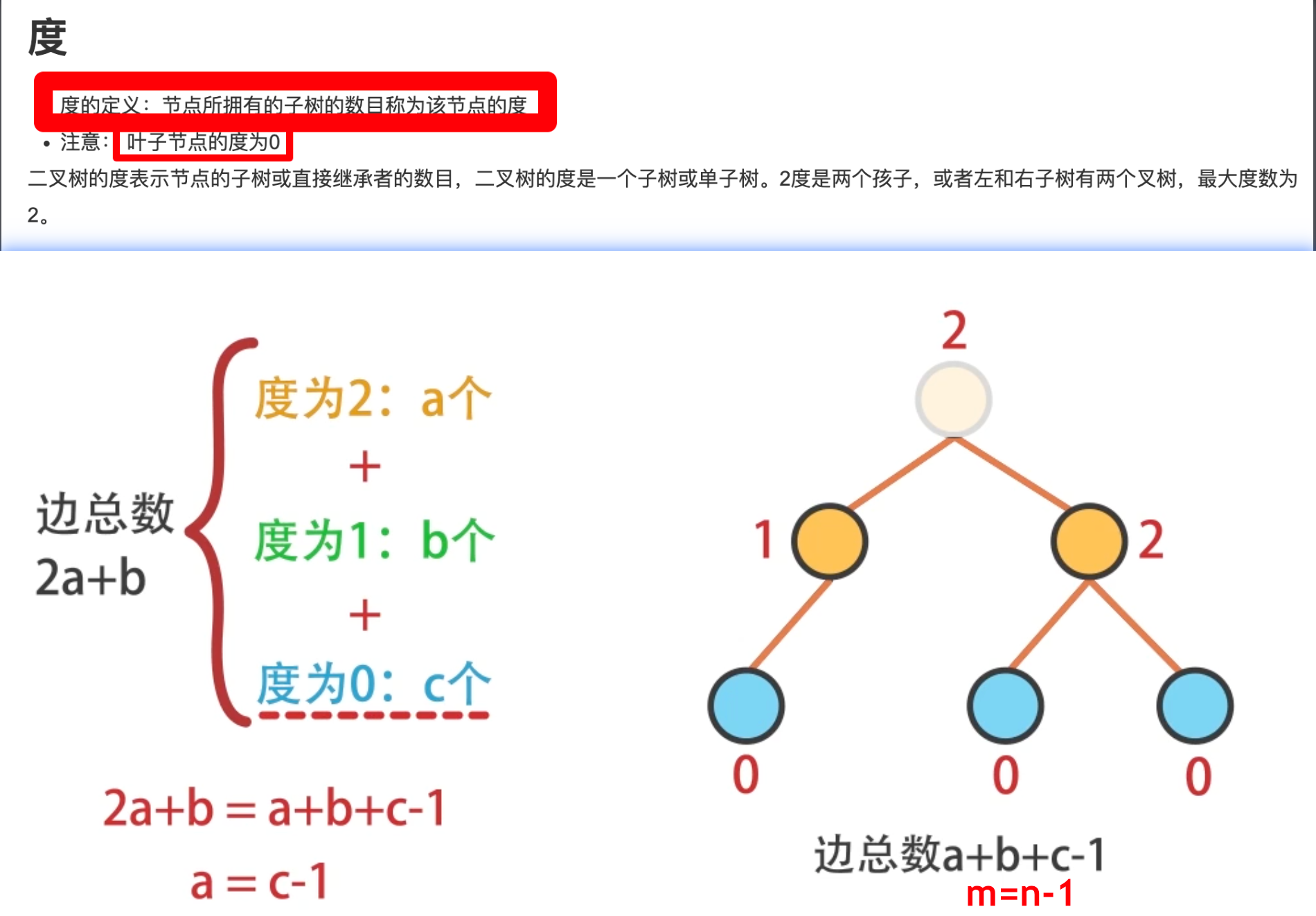
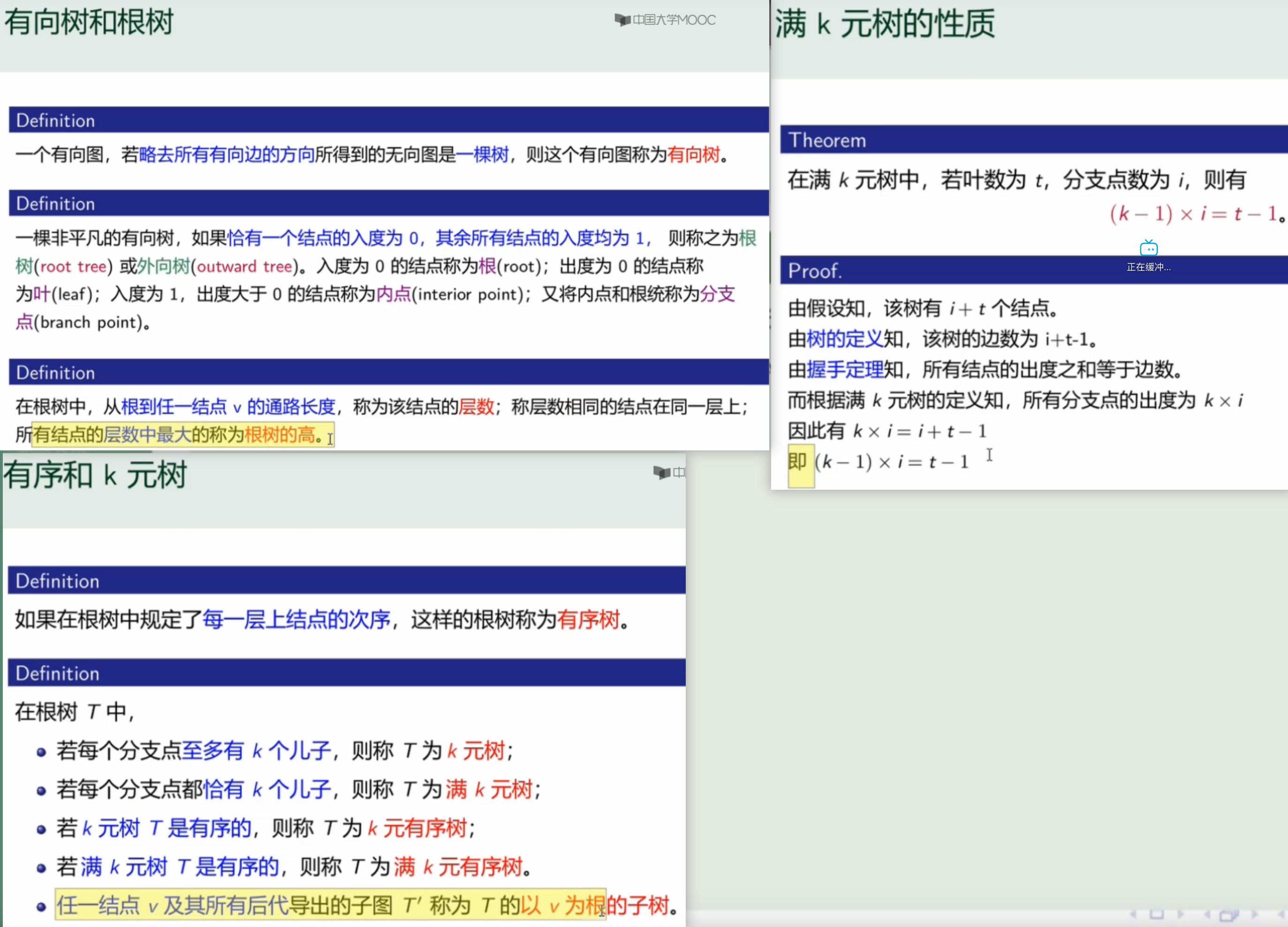
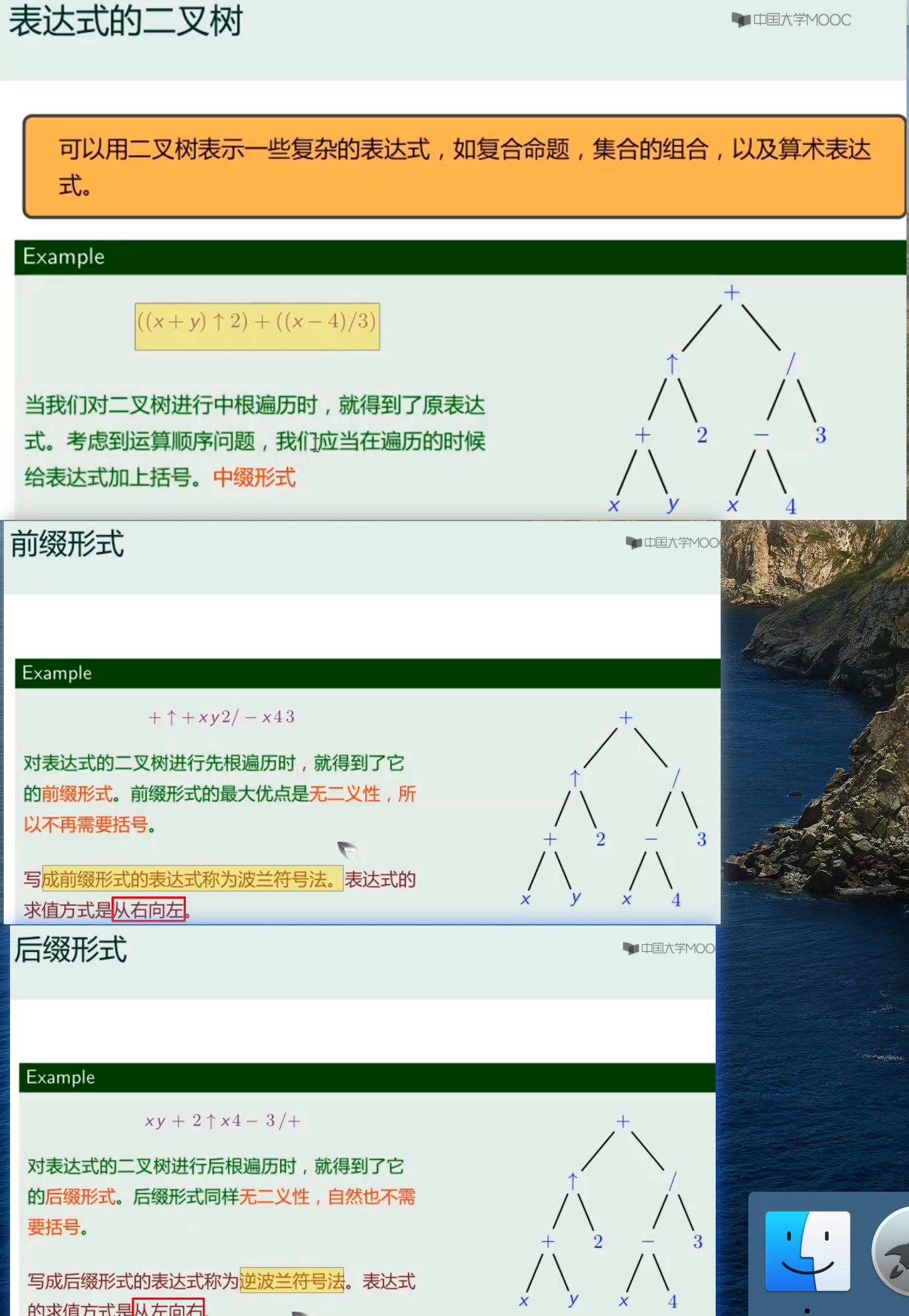
- 在二叉树中,总是认为叶子结点的度为0:
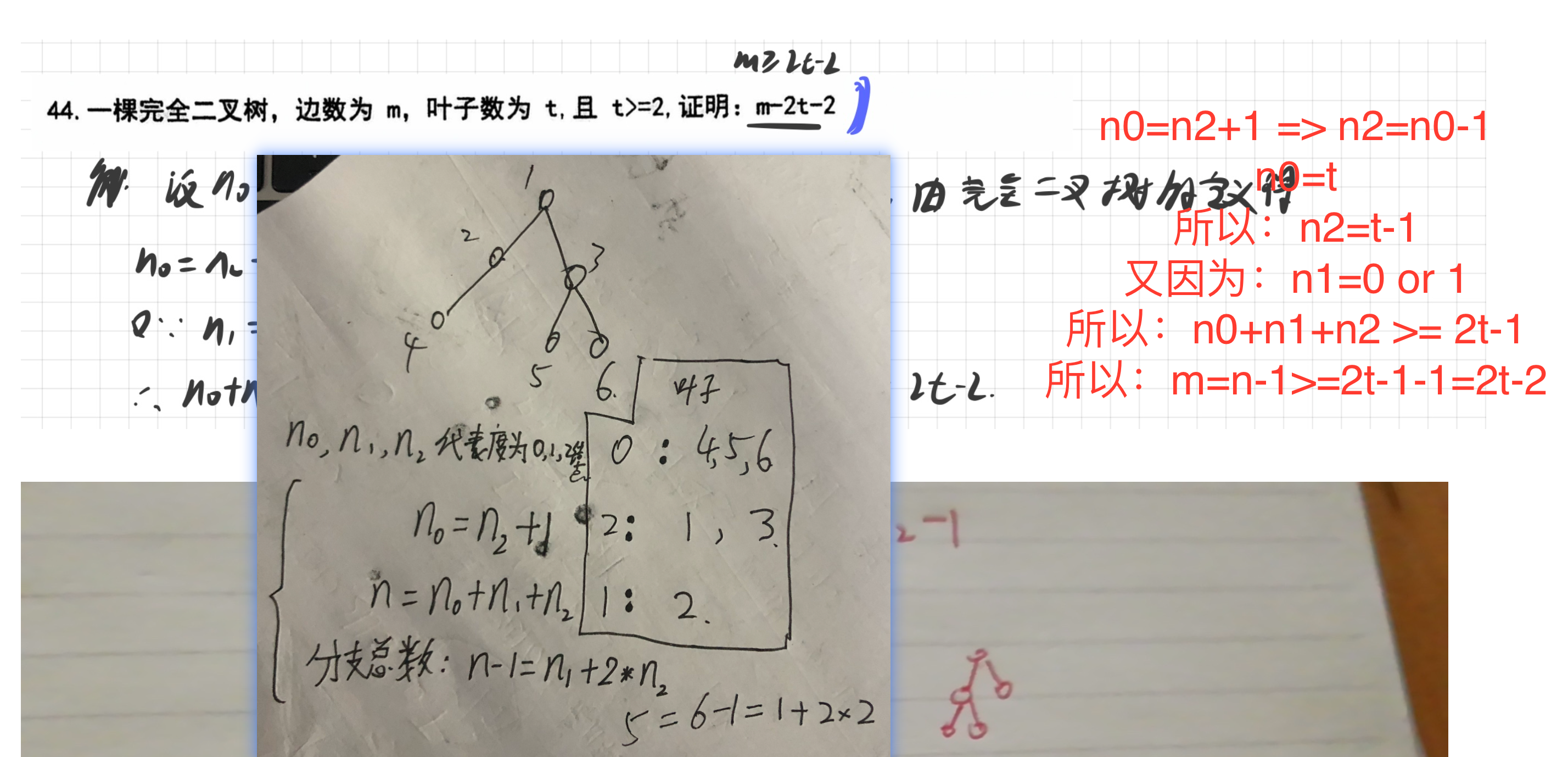
完全二叉树的定理做题
- 在二叉树上的第i层上至多有 个节点(i>=1)
- 深度为k的二叉树至多有 个节点(k>=1)
- 具有n个节点的完全二叉树的深度为 └log2n┘+ 1
- 度为1的顶点数为0或1
- 分别代表节点的度数为0、1、2。
- n为总结点数
- ;
- 在离散数学中的树,认为叶子的度为1,且符合握手定理
最小生成树
-

-
-
-
平凡图只有一个节点,没有边
-
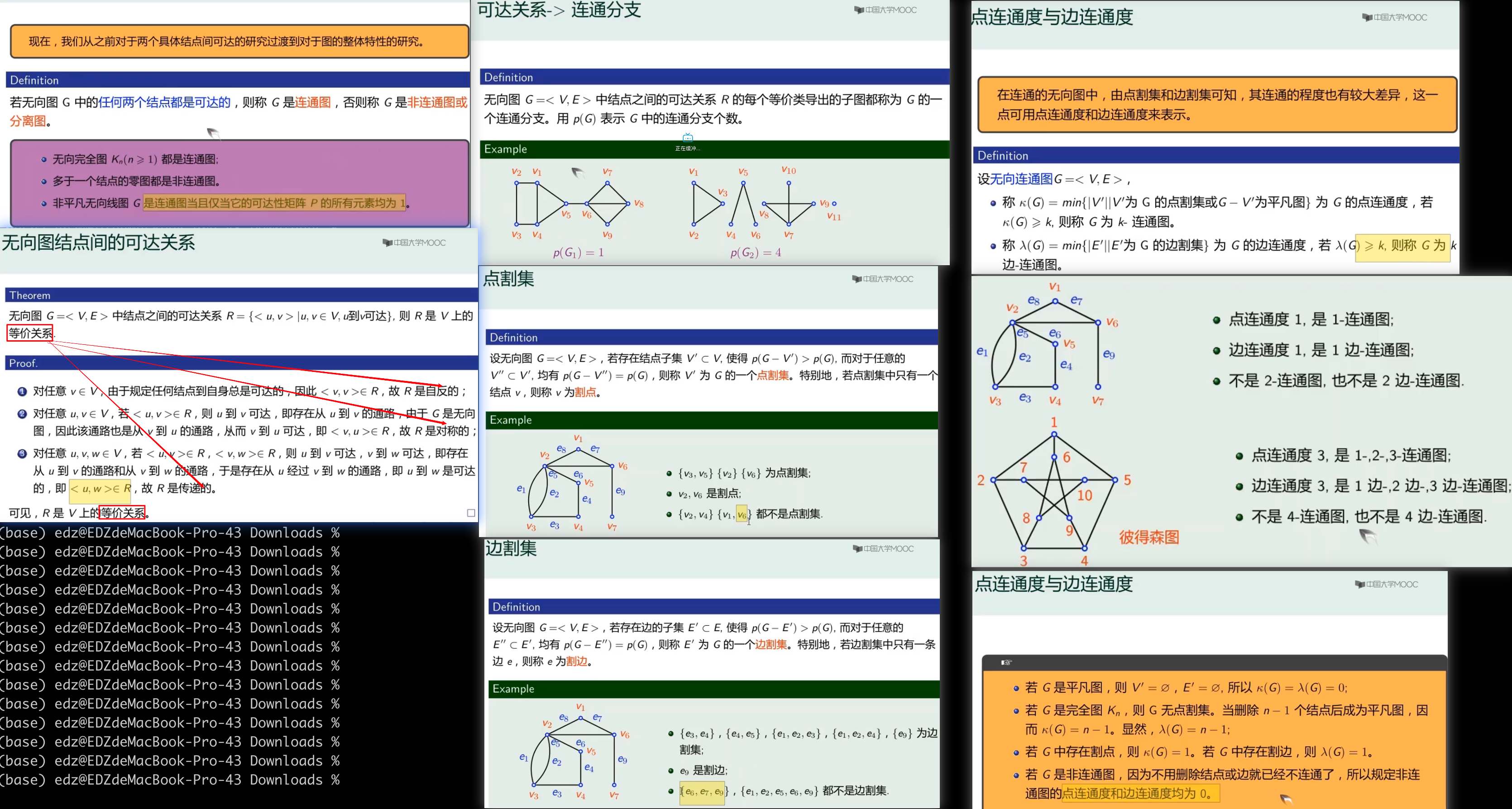
连通分支,--> 去掉某个节点后,图变成了独立的几块
-
-
-
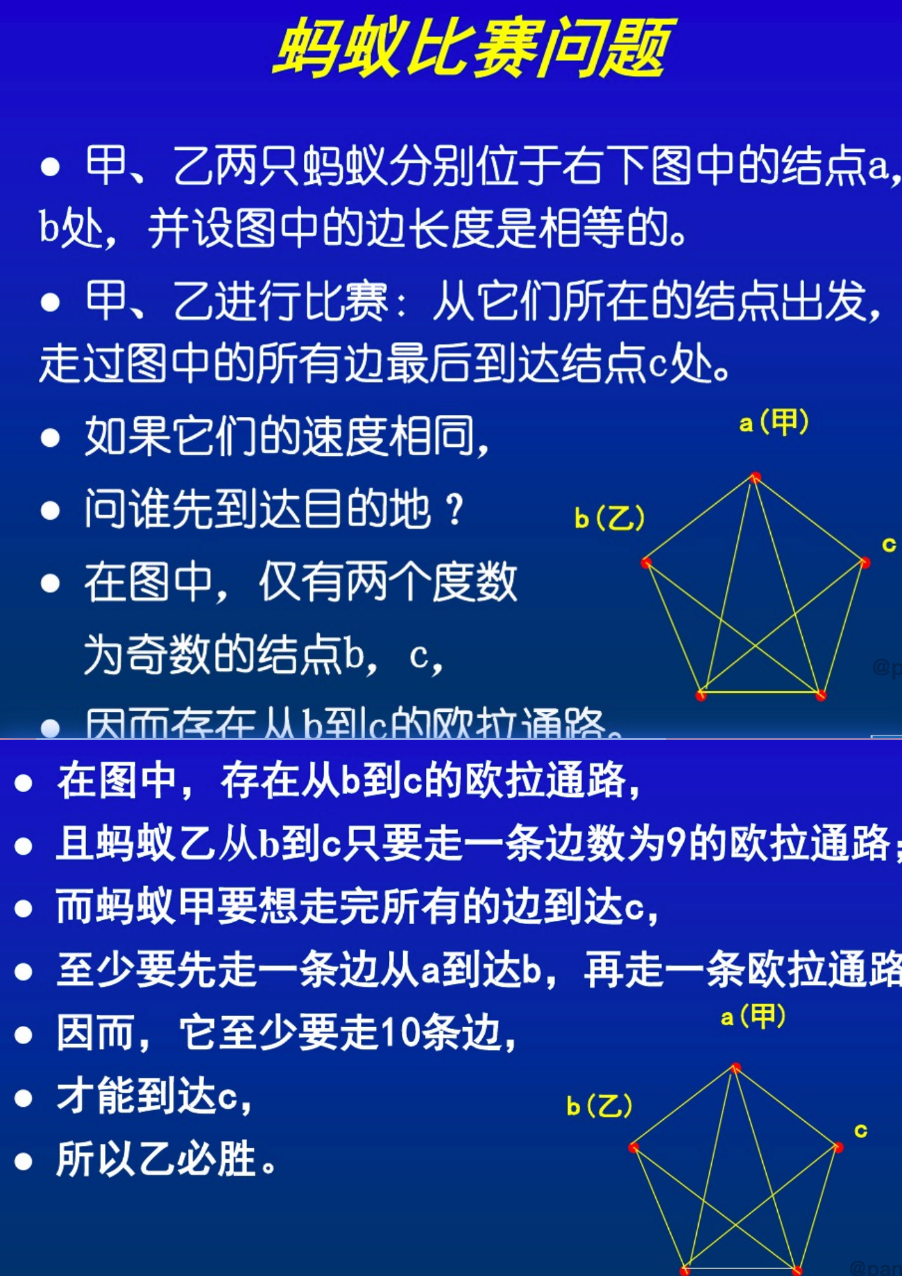
平⾯图、偶图(⼆部图)和欧拉回路、欧拉通路的判定
-
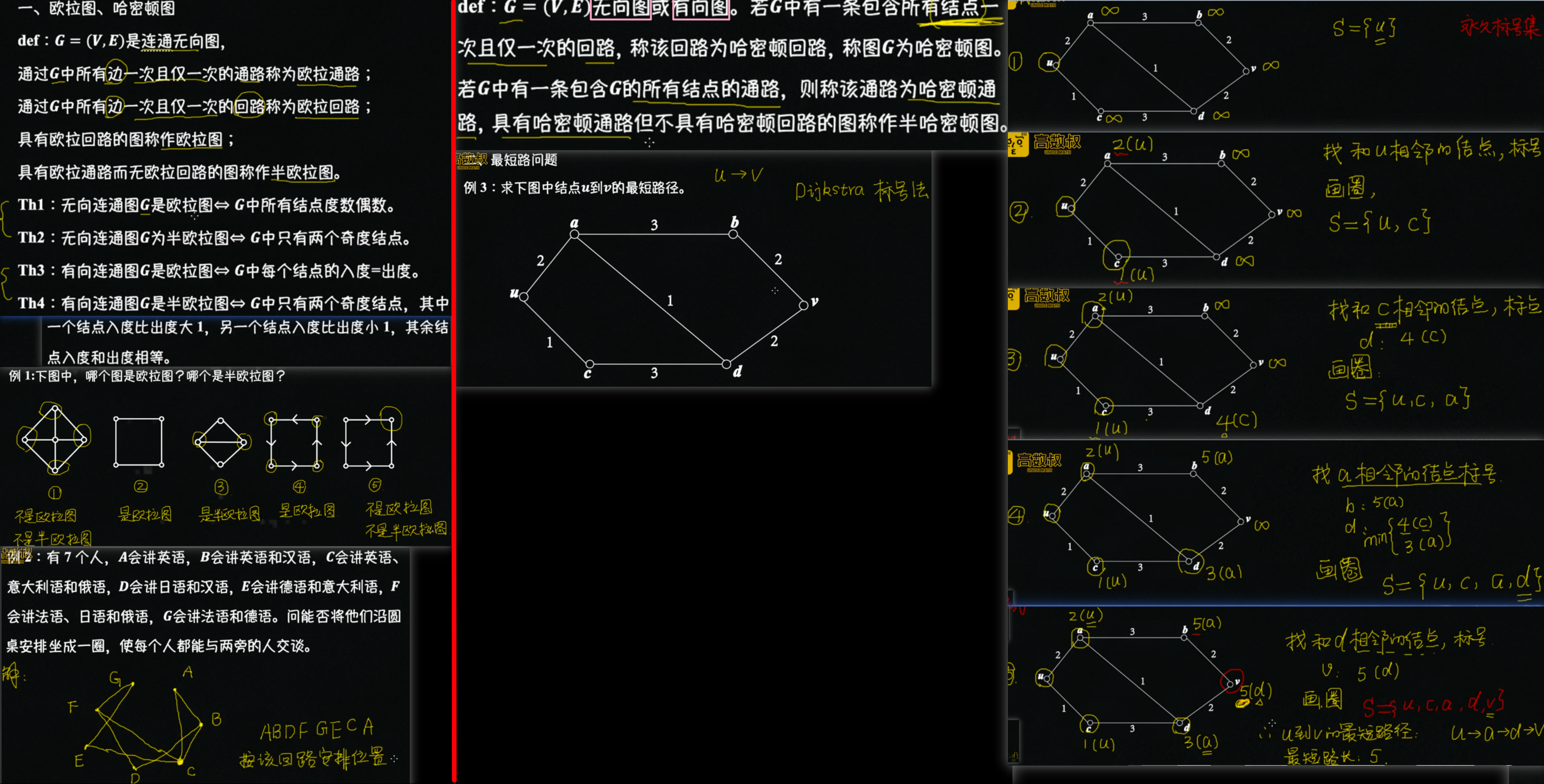
判断哈密顿图的必要条件:
- 若无向图G=<V,E>为哈密顿图,则图G中无割点。
-
- 割点:如果去掉一个点以及与它连接的边,该点原来所在的图被分成两部分(不连通),则称该点为割点。
-
- 割边:如果去掉一条边,该边原来所在的图被分成两部分(不连通),则称该点为割边。
-

- 若无向图G=<V,E>为哈密顿图,则图G中无割点。
-
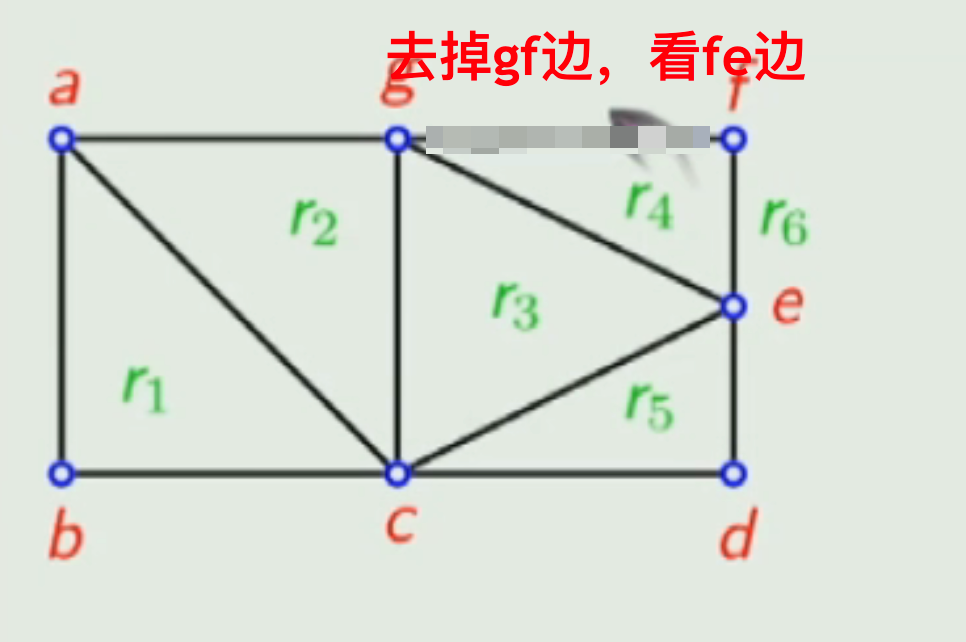
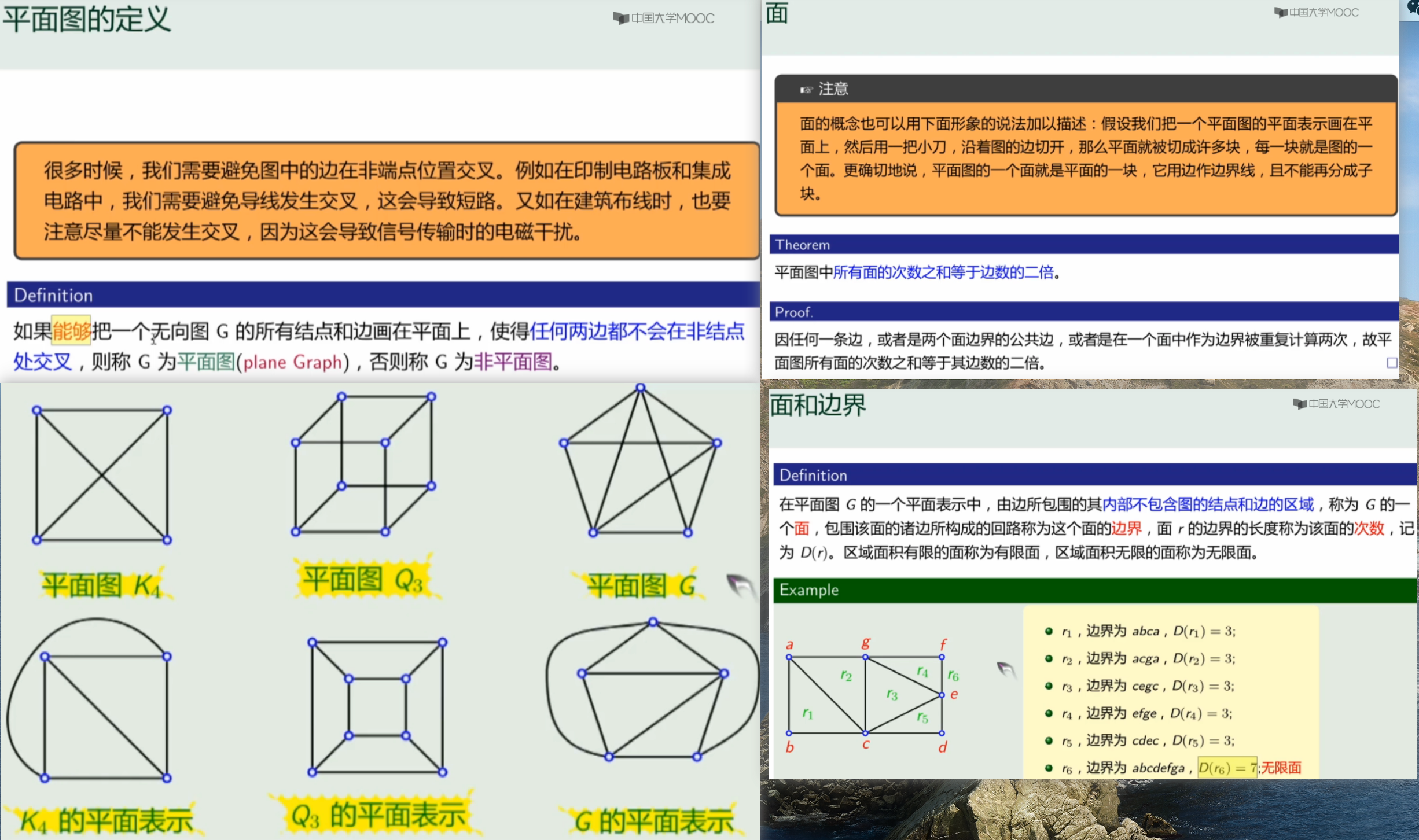
欧拉公式:
n-m+r=2:n个结点、m 条边和- 有多个连通分支:
- 平面图中:⚠️这是错误的
,应该是;⚠️这里没有说某个边一定对应两个面->只能说:- 因任何一条边(或者是两个面边界的公共边,或者是在一个面中作为边界)被重复计算两次,故平 面图所有面的次数之和等于其边数的二倍。
- 因任何一条边(或者是两个面边界的公共边,或者是在一个面中作为边界)被重复计算两次,故平 面图所有面的次数之和等于其边数的二倍。
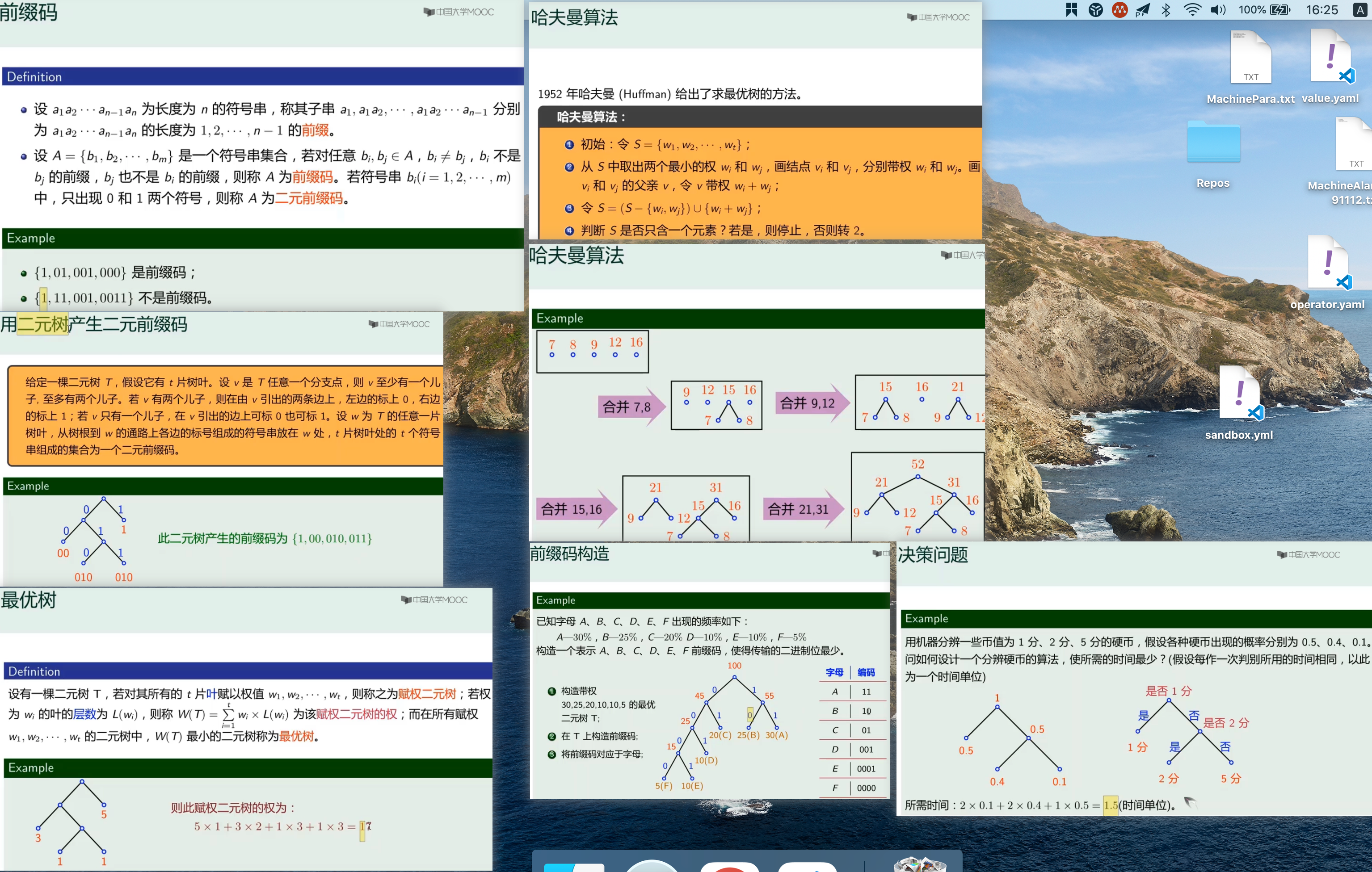
欧拉图
哈密顿图
偶图(二分图/二部图);有个偶字,所有回路都是偶数
-
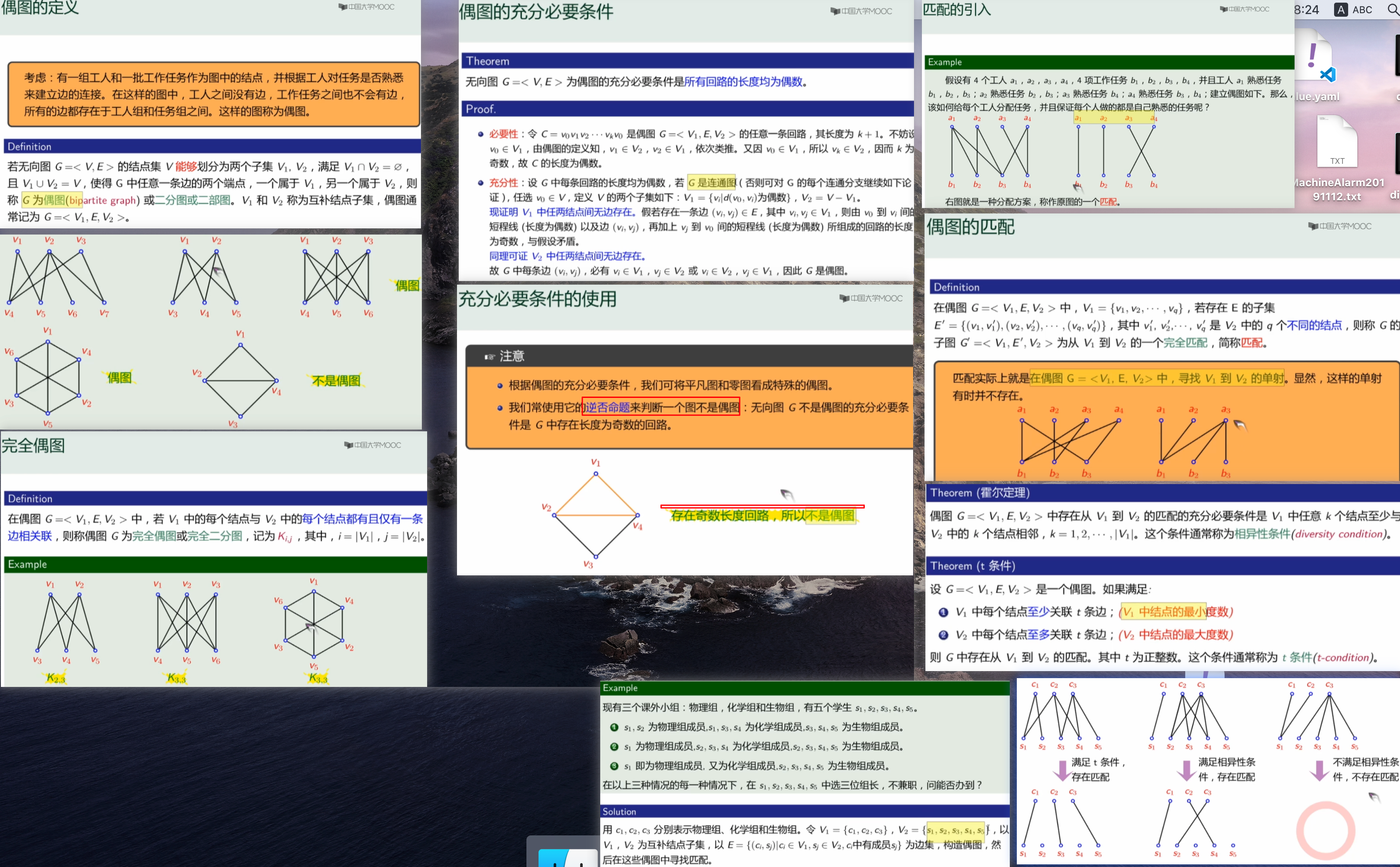
-
平面图
-
欧拉公式
简单图不能够有自回路/平行边
题型
连通判断
-
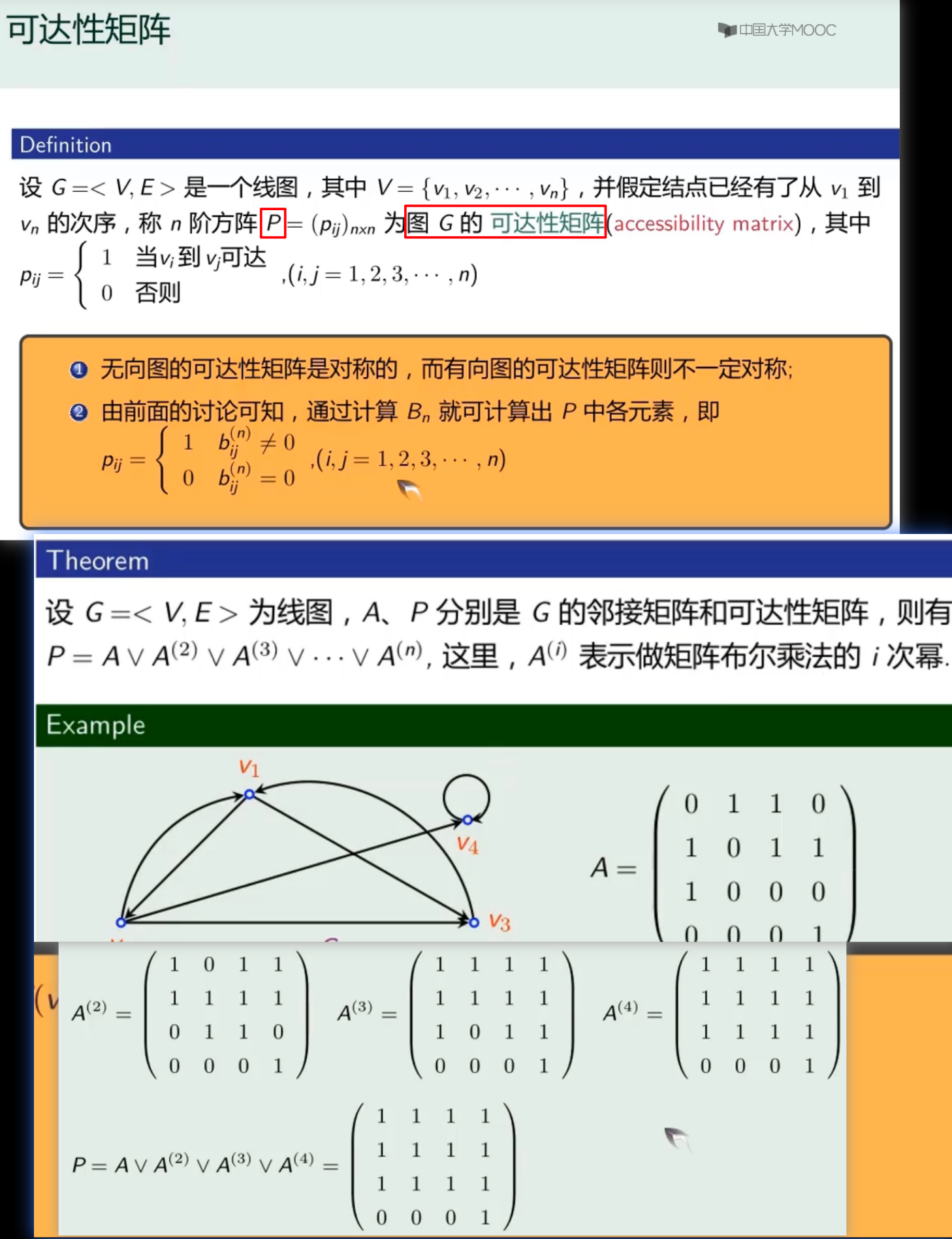
可达性矩阵P:用邻接矩阵求得,利用传递性,直到N次方, 起来就行(如果中间有和前面一样的就中止)
-
强连通:求p,如果不是全1,则不是强连通图
-
弱连通图:求邻接矩阵 ,再对它求可达性矩阵,所有元素都是1就是弱连通图
-
单向连通图:求 ,如果除了对⻆线全为1,则是单向连通图
-
强连通分图:求 ,得到的对称矩阵,就可以算那些是连通的
- TODO
求度数序列是否可图
- 可图(Graphic): 就是如果一串度序列可以逆向生成出图,就是可图的。而判断一个序列是否是可图的,则由Havel-Hakimi定理判断。
- 什么是可图,那需要先说一下度序列。
- 度序列是把图的多有顶点度数排列成一个序列s,则称s为图G的度序列。
- 度序列可以是按照顶点的顺序排列,也可以按照递增、递减的顺序排列。所谓的可图,是建立在度序列的基础上的。
- 序列是可图的:一个非负整数组成的有限序列如果是某个无向图的度序列,则称这个序列是可图的
- 什么是可图,那需要先说一下度序列。
4,判定过程:(1)对当前数列排序,使其呈递减,(2)从S【2】开始对其后S【1】个数字-1,(3)一直循环直到当前序列出现负数(即不是可图的情况)或者当前序列全为0 (可图)时退出。
- 握手定理1:度数和必须为偶数
- 握手定理2(Havel-Hakimi定理):由非负整数组成的有限非递增序列,S={d1,d2,d3...dn},当且仅当S1={d2-1,d3- 1...d(d1+1),d(d1+2)......dn}也是可图的,也就是说,序列S1也是由 非负整数组成的有限非递增序列,S1是由S的删除第一个元素d1之 后的前d1个元素分别减一后得到的序列。
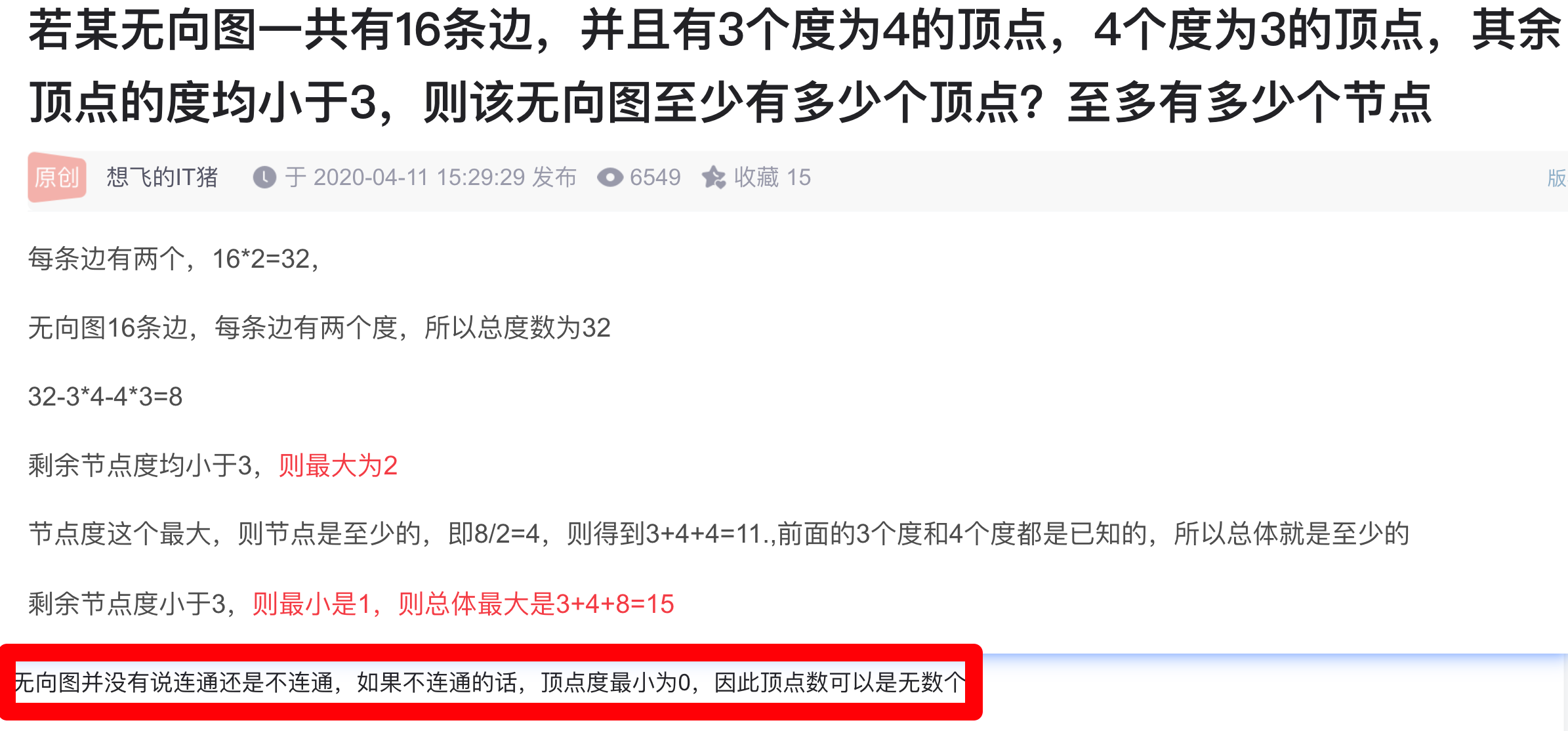
至少有多少个结点
代数系统
-
((fog)oh)(x)=h(g(f(x))) -

-
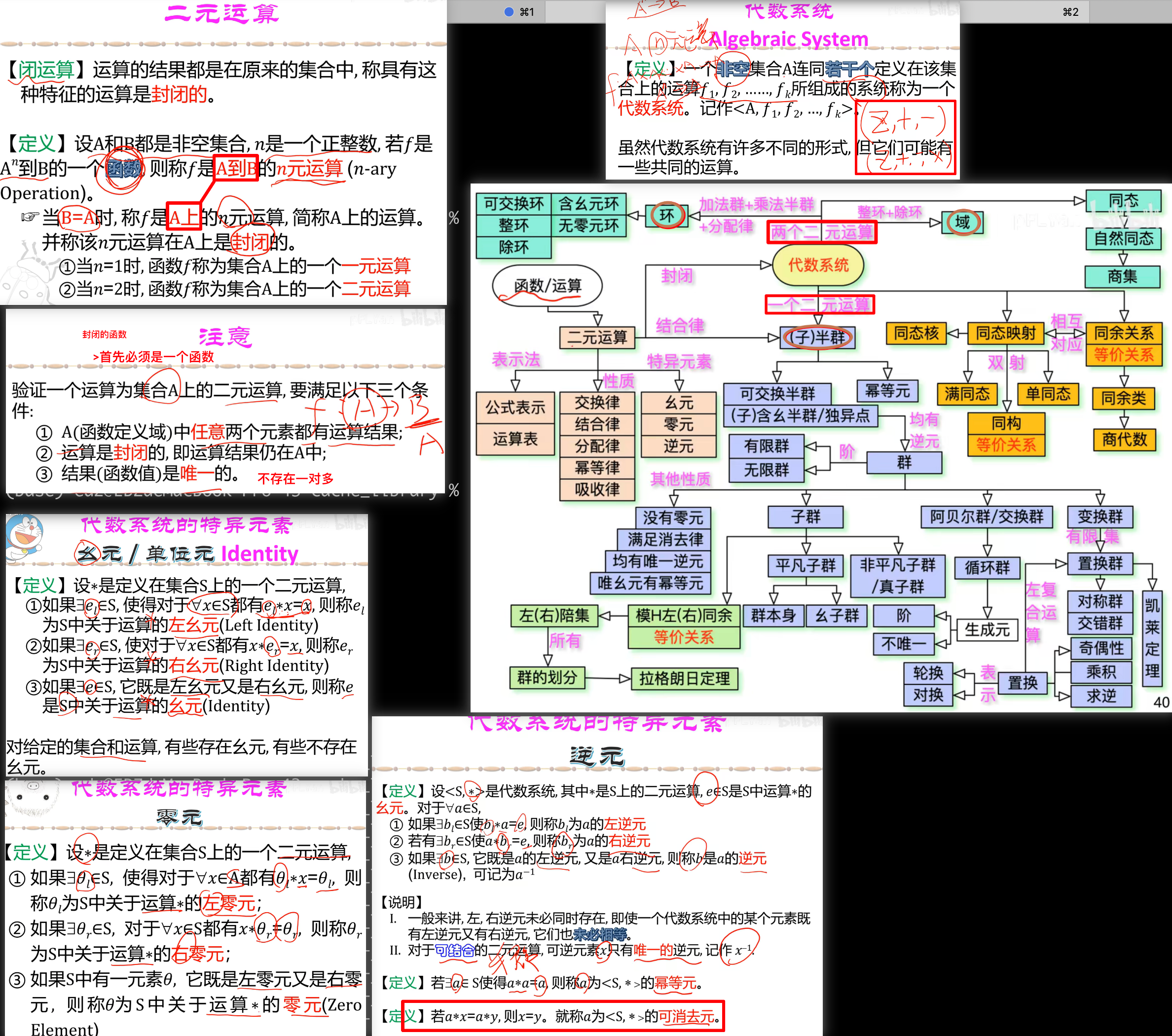
幺元-1元:1乘以任何元素等于自己
零元-0元:0乘以任何元素都等于零元
-
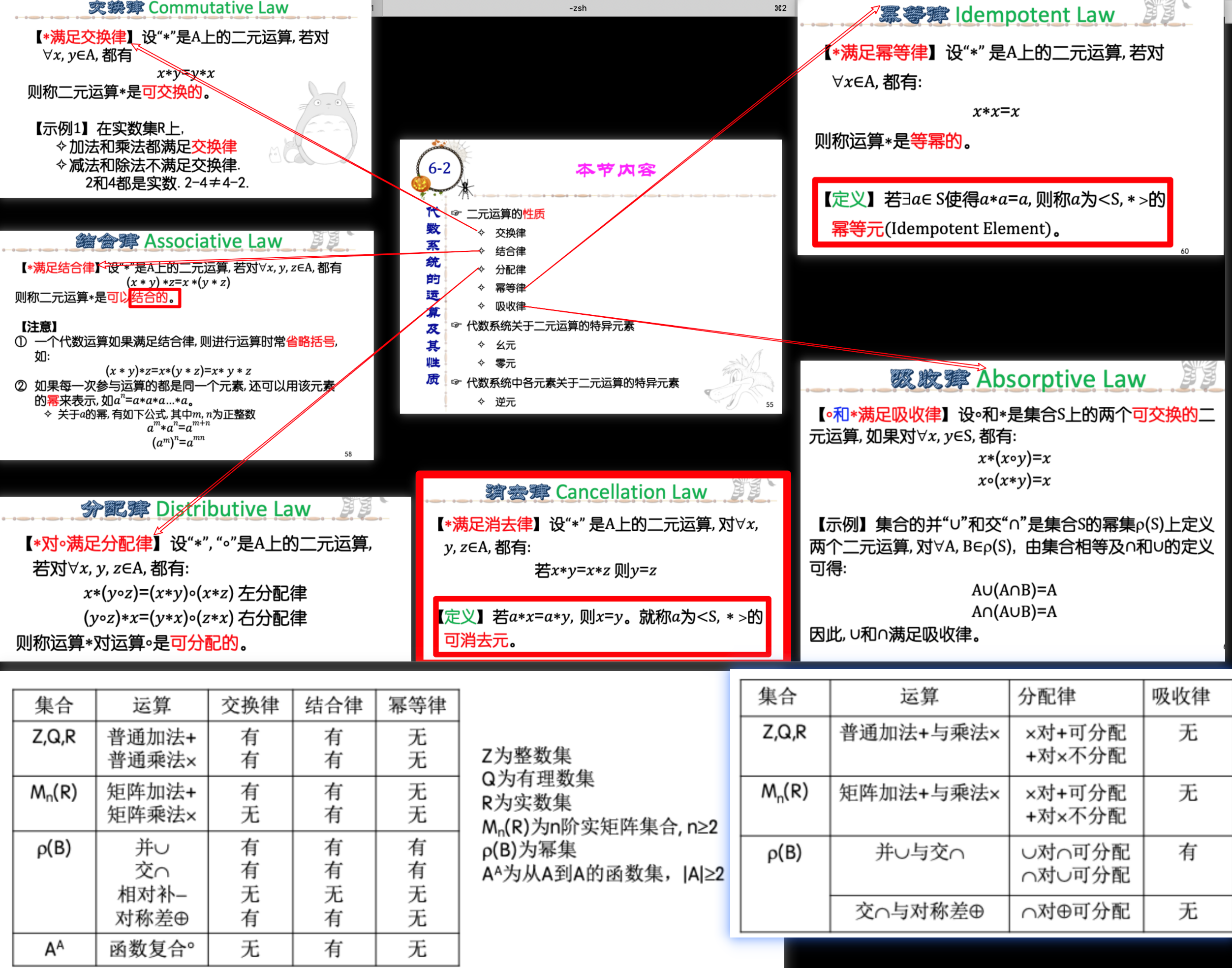
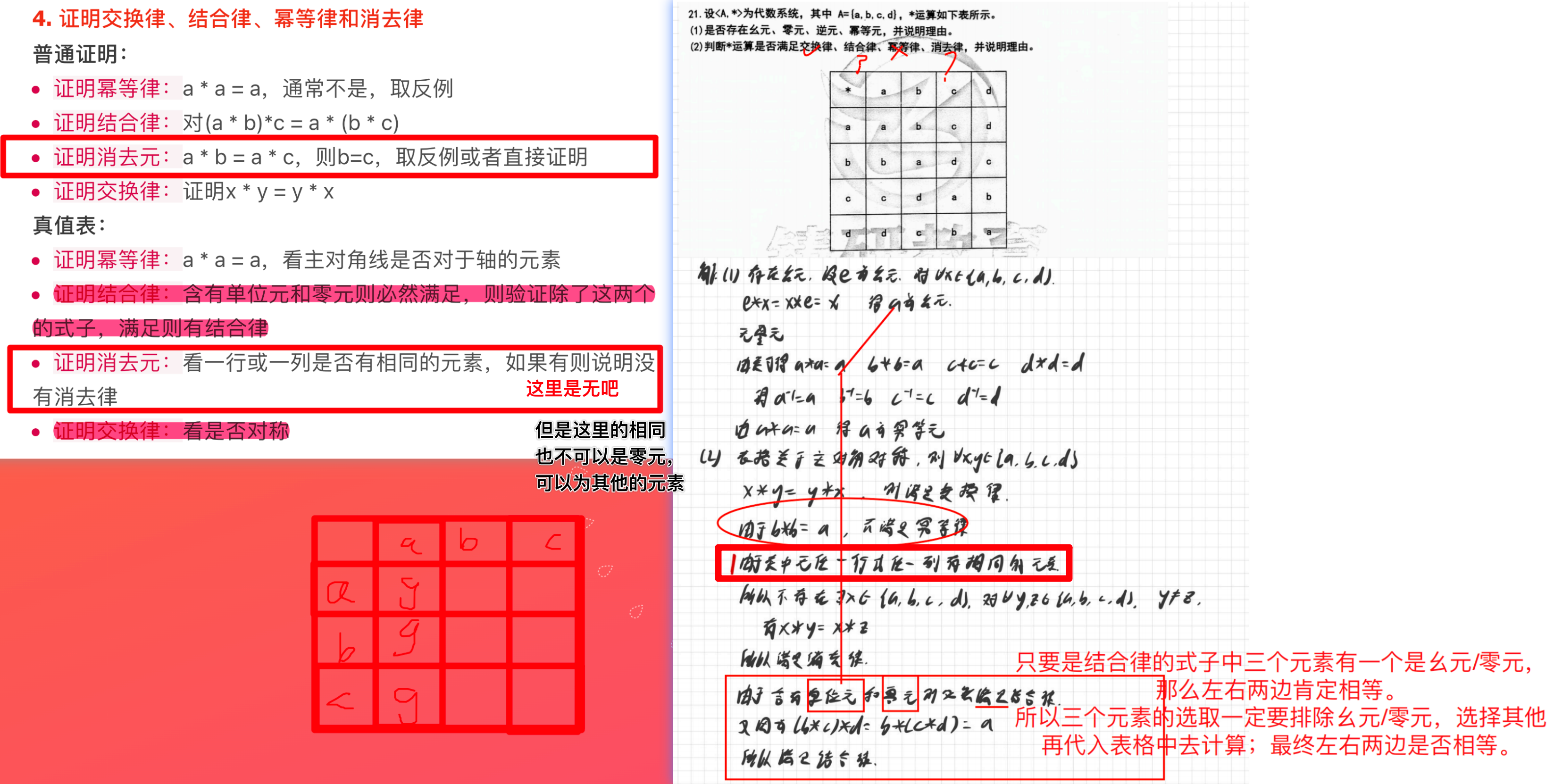
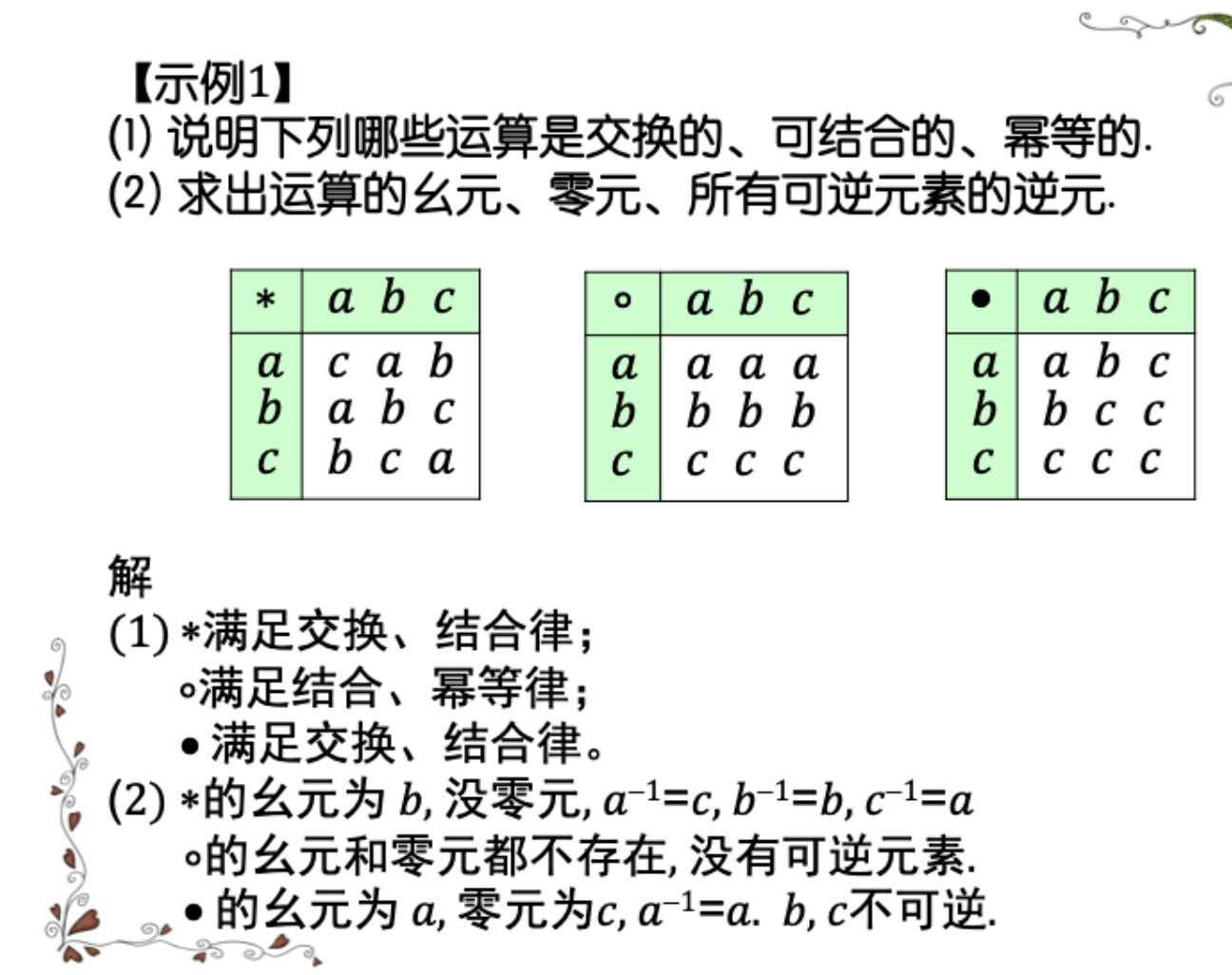
性质
-
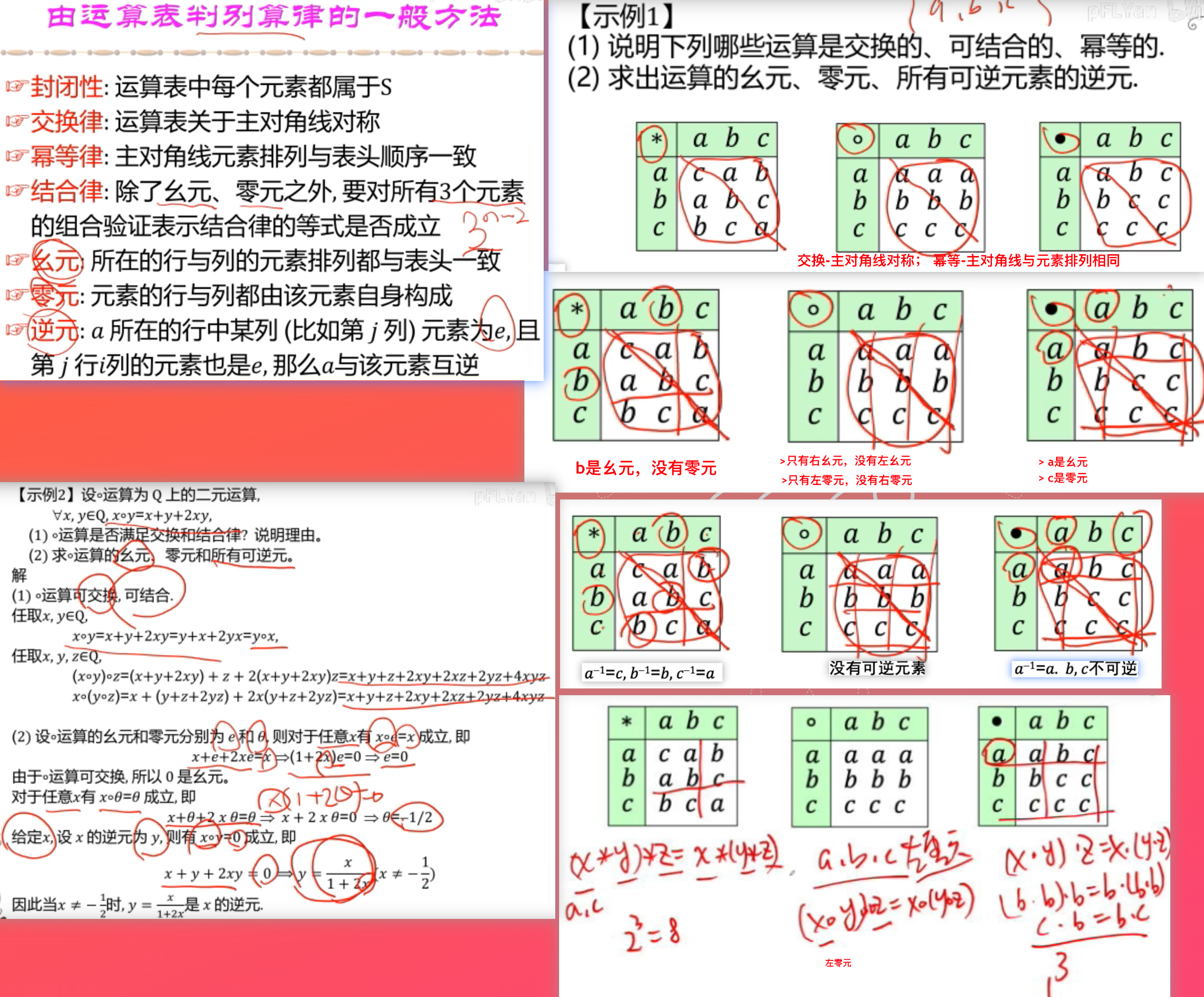
半群
群
求子群
- 求某个数的正因子: 1和它自身是一定在的,然后分解它,找出所有的因子就行;比如15,{1,15},然后3*5=15;所以{1,3,5,15}

- 8的正因子: -> 0,1,2,3四个正因子->
- 15的正因子: -> 0,1 | 0, 1 => 2*2 = 4五个正因子-> = {1,5,3,15}
拉格朗日定理
设 < H , ∗ > <H,*><H,∗> 是群 < G , ∗ > <G,* ><G,∗>的一个子群,则子群 H 的阶 m 必然能够整除群 G 的阶 n, 即m∣n。- https://blog.csdn.net/qq_25847123/article/details/100318620
群的阶
用群的阶/子群的阶


- 所以就成功了,反过来想,先用群的阶/子群的阶 === 子群中最小的那个 --> 由它推出剩下的
周期
补充个集合非空
群的阶
有限群是具有有限多个元素的群。其所包含的个数,称为有限群的阶。
假若群G是一个有限群,则组成G的元的个数为G的阶,记为|G|。
比如 素数阶的有限群都是循环群。
生成元
-
群中元素可以由最小数目个群元的乘积生成,这组群元称为该群的生成元,生成元的数目为有限群的秩。
-
秩:生成元的数目为有限群的秩。有限群的生成元的选择不唯一,但秩不变。
证明群<H, *>是群<G, *>的子群
- 判定定理:设S是群<G, *>的非空子集,S是群G的子群的充分必要条件是:对所有a,b∈S,都有
左右陪群
同态/同构
快速回顾
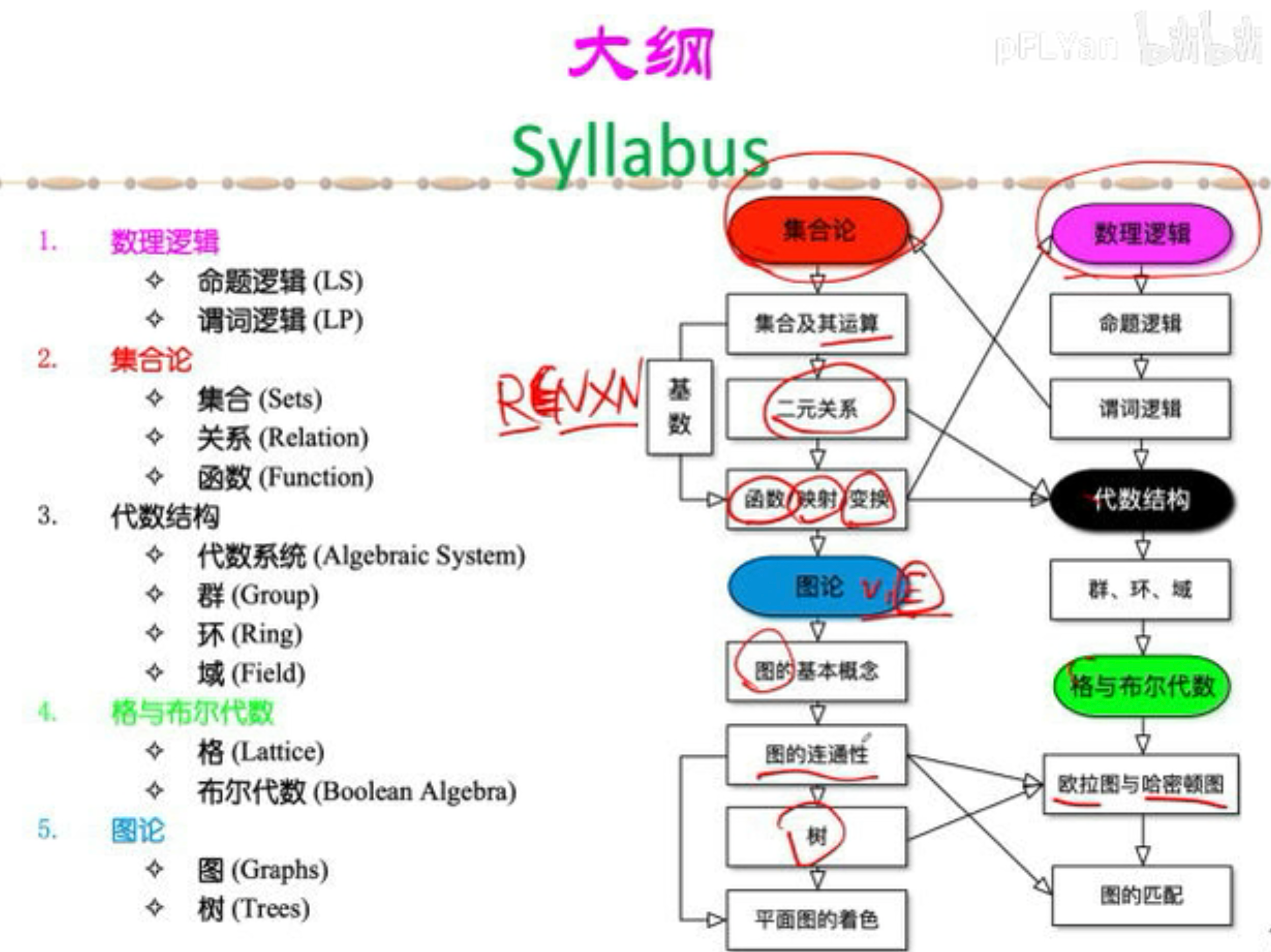
附录
-
https://www.bilibili.com/video/BV1W44y1J7LF/?spm_id_from=pageDriver
-
网盘:https://www.dashengpan.com/#/main/search?keyword=离散数学&searchtype=0
-
离散数学:绩加加 https://www.bilibili.com/video/BV1Hi4y1o7Mo?spm_id_from=333.999.0.0
-
代数系统:https://www.bilibili.com/video/BV1da4y1W7BV?spm_id_from=333.337.search-card.all.click
-
质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数(规定1既不是质数也不是合数)
-
整除: