LR(0)

下面用一个非常简单的例子来介绍如何使用形态和状态来构造 LR(0) 分析。语法为：

1
2
3

S -> A
A -> aBd
B -> bc

首先，求出该语法的起始状态 I0

1
2
3

I0:
    S -> .A
    A -> .aBd

对语法中的所有符号X(S, A, B, a, b, c, d), 求出I0遇到X的后继状态NEXT(I0, X), 若NEXT(I0, X)不是空集, 则将其添加到状态转移图中，如下：

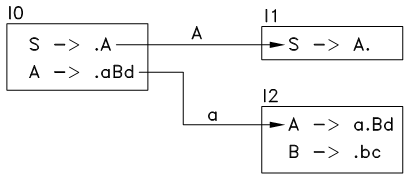图11.2 状态转移图1

按以上方法，不断的生成新的状态，直到不再出现新的状态，最终如下：

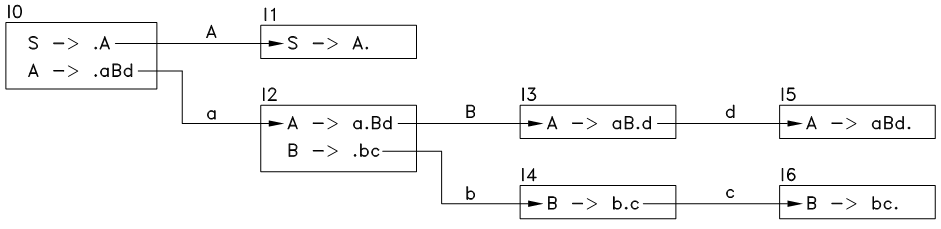图11.3 状态转移图2

显然，解析的最开始的时候，没有读入任何符号，此时的状态为I0，每读入一个符号，则转移到另一个状态.

这个状态转移图似乎和有限状态自动机的运行图很相似，那么，解析的过程是不是就是用有限状态自动机来依照上面那个图来运行一遍？答案是不行的。上一章已经说过了，有限状态自动机只能解析正则语言，无法解析复杂的上下文无关语言。为了解析上下文无关语法，我们需要一种更强大的自动机，这种自动机不仅仅需要记住它当前的状态，还需要记住它的历史路径，记住它是如何到达当前状态的。

简单来说，这种自动机含有一个栈，它的大致的运行机制为：

在读入符号之前，将初始状态I0压入栈顶，之后，每读入一个符号，它就转移到下一个状态（将下一个状态压入栈顶），当它转移到一个可折叠状态时，它执行一个折叠动作（将前面的一些状态出栈、再压入下一个状态），一直到它折叠得到的非终结符是起始符号，且下一个符号是 $ 时，它才终止运行。

上面这段描述只是一个大致的运行流程，里面有两个重要的问题没讲清楚，一个是转移和折叠动作的具体操作步骤，另一个什么是可折叠状态.

我们先把后一个问题讲清楚： 可折叠状态(reduceable state):只含有一个形态的状态，且此形态为可折叠形态，如图11.3中的I1, I5和I6.

附录

形态和状态

LR(0) 分析法是一种最基本的 LR 分析法，其构造过程中的核心是状态 和 形态, 以下给出相关术语的正式定义，并介绍如何构造 LR(0) 分析器.

形态

形态（configuration）:一个产生式的解析程度，用一个产生式加一个位置黑点来表示，例如，产生式 A -> XYZ 有 4 中可能的解析程度:

1
2
3
4

A –> •XYZ
A –> X•YZ
A –> XY•Z
A –> XYZ•

位置黑点表示本产生式解析过程中前进到的位置，比如一个产生式: S -> abc ，则它最开始的形态为 S -> •abc ，读入一个 a 后其形态变为 S -> a•bc ，再读入一个 b 后变为 S -> ab•c 。

形态一般用大写字母 C 表示。

需要注意的是，如果一个产生式的右边是空串，如 A -> ε ，那么形态 A -> •ε 和 A -> ε• 是同样的形态，一般都只采用后一种表示方式。

起始形态

产生式的起始形态（start configuration of a production）:位置黑点位于该产生式右边的第一个符号的前面的形态，如： A –> •XYZ.

已完成形态(可折叠形态[不是可折叠状态])

产生式的已完成形态（complete configuration of a production）:位置黑点位于该产生式右边的最后一个符号的后面的形态，如： A –> XYZ• 。也称为可折叠形态（reduceable configuration）.

形态的转移

形态的转移 ： 当一个形态 A –> X•YZ 遇到一个符号 Y 时，它就转移到下个形态： A –> XY•Z ，见下图： 图11.1 形态转移示意图

若记 C = [A -> X•YZ] ， C’ = [A –> XY•Z] ，称形态 C’ 为形态 C 遇到符号 Y 时的 后继形态（successor configuration） ，可写为 NEXT(C, Y) 。若形态 C 遇到的符号 X 不等于其位置黑点后面的符号时，称 NEXT(C, X) 不存在。

延伸形态

延伸形态（extended configuration） ：对于形态 A –> v•Yw ，若 Y 为非终结符，且 Y -> u ，则形态 Y -> •u 是形态 A –> v•Yw 的延伸形态，进一步的，若 u 的第一个符号为非终结符 Z ，且 Z -> u1 ，则形态 Z -> •u1 既是 Y -> •u 的延伸形态，也是 A –> v•Yw 的延伸形态。

例如，语法：

1
2
3

S -> Ab
A -> Bc
B -> d

A -> •Bc 和 B -> •d 都是 S -> •AB 的延伸形态。

这里要注意的是： 延伸的方向是单向的 ，上面这个语法中，A -> •Bc 是 S -> •AB 的延伸形态，但 S -> •AB 不是 A -> •Bc 的延伸形态，只有 B -> •d 才是 A -> •Bc 的延伸形态。

形态集合

形态集合（configurating set） ： 一个由有限个形态组成的集合.

形态集合的闭合

形态集合的闭合（closure of a configurating set） ： 形态集合的闭合就是把这个集合里所有形态的所有延伸形态全部添加进这个集合。按以下步骤进行（设该集合名为 I ）：

  1. 遍历 I ，对 I 中的每一条形态A -> u • v ，若 v 的第一个符号为非终结符 B ，则将其所有的产生式的起始形态添加进 S ，即若B -> u1 | u2 | ... | un, 则将 B -> • u1, B -> • u2, ..., B -> • un添加进I.
  2. 重复（1），直到不再出现新的形态。

闭合操作的得到的新集合 I’ 称为原集合 I 的 闭包集合 ，记为 CLOSURE(I) 。

状态

状态(state):进行过闭合操作的形态集合，一般用大写字母I表示，也就是说，若形态C属于状态I ，则C的延伸形态也属于I.

起始状态(记为I0)

上下文无关语法的起始状态（start state of a CFG） ： 若一个 CFG 的起始符号 S 的所有产生式为 S -> u1 | u2 | ... | un ，且 S 不位于任何产生式的右边，则其起始状态(记为I0)是这些产生式的起始形态的集合的闭包集合，即：I0 = CLOSURE( { [S-> • u1], [S-> • u2], ... [S-> • un] } )

例如，语法：

1
2
3

S -> A
A -> aBd
B -> bc

it的起始状态:

  • I0 = CLOSURE( {[S-> • A]} )
    • CLOSURE( {[S-> • A]} ) ==> S-> .aBd ==> a是终结符.
  • I0 = { [S-> • A], [A-> • aBd] }

为什么没有[B -> bc]?

起始状态可以认为是语法解析的初始状态，此时尚未读入任何符号，因此起始符号的所有产生式都处在其初始形态。

上面提到了，要求 S 不位于任何产生式的右边。如果 S 位于某条产生式的右边，则这个状态可能不能代表语法解析的初始状态。例如，对于语法： S -> a | aS 。当解析句子 aaa 的时候，状态{ [S-> • a], [S-> • aS] }，可能代表 ” • aaa” 的状态，也可能代表 “a • aa” 的状态 （这里的 ” • ” 表示已读入符号和未读入符号的分割位置）。

为了保证起始符号不位于任何产生式的右边，一般在语法中增加一个非终结符 S’ 和一条产生式 S’ -> S ，而用这个 S’ 作为起始符号。如前面这个语法 S -> a | aS 可以改为：

1
2
3

S' -> S
S  -> a
S  -> aS

此时的状态{ [S’-> • S], [S-> • a], [S-> • aS] }就只能代表” • aaa”的状态了.

形态集合的闭合(closure of a configurating set)

形态集合的闭合（closure of a configurating set） ： 形态集合的闭合就是把这个集合里所有形态的所有延伸形态全部添加进这个集合。按以下步骤进行（设该集合名为 I ）：

  • 遍历 I ，对 I 中的每一条形态 A -> u • v ，若 v 的第一个符号为非终结符 B ，则将其所有的产生式的起始形态添加进 S ，即若 B -> u1 | u2 | … | un ，则将 B -> • u1, B -> • u2, …, B -> • un 添加进 I 。
  • 重复（1），直到不再出现新的形态。

起始状态起始状态 闭合操作的得到的新集合 I’ 称为原集合 I 的 闭包集合 ，记为 CLOSURE(I) 。

可折叠状态

可折叠状态（reduceable state）:只含有一个形态的状态，且此形态为可折叠形态(不是状态)，如图11.3中的 I1 、 I5 和 I6.

形态（configuration）:一个产生式的解析程度，用一个产生式加一个位置黑点来表示

一个产生式===>plus .===>形态 形态集合===>闭合操作===>状态

  • reference:形态集合, 形态集合的闭合.
  • 状态(state):进行过闭合操作的形态集合，一般用大写字母I表示，也就是说，若形态C属于状态I ，则C的延伸形态也属于I.

自动机的具体操作流程为：

  • （1） 将初始状态 I0 压入栈顶；
  • （2） 读入下一个符号 x ，相当于调用一次 x = yylex() ，有两种情况：
    • （2.1） x 不是终结符：输入不合语法，执行 deny 操作，终止解析；
    • （2.2） x 是终结符：转到（3）；
  • （3） 置 X = x ；
  • （4） 设栈顶状态为 I ，有以下两种情况：
    • （4.1） I 不是可折叠状态，有以下三种情况：
      • （4.1.1） NEXT(I, X) 存在（设为 I’）、 X 为终结符：执行 shift I’ 操作，将 I’ 压入栈顶，转到（2）；
      • （4.1.2） NEXT(I, X) 存在（设为 I’）、 X 为非终结符：执行 goto I’ 操作，将 I’ 压入栈顶，转到（3）；
      • （4.1.3） NEXT(I, X) 不存在：输入不合语法，执行 deny 操作，终止解析；
    • （4.2） I 是可折叠状态，设 I 里面的形态对应的产生式为 A -> X1 X2 … Xn ，有以下三种情况：
      • （4.2.1） A != S ：执行 reduce (A, n) 操作，将栈顶及以下 n 个状态出栈，置 X = A ，转到（4）；
      • （4.2.2） A == S 、 X != $ ：输入不合语法，执行 deny 操作，终止解析；
      • （4.2.3） A == S 、 X == $ ：输入合法，执行 accept 操作，终止解析。

上面这个语法中的每一行形如 “语句 -> 主语 谓语 宾语” 的式子称为 产生式（production）。

  • 产生式左侧的符号（语句、主语、谓语和宾语）称为 非终结符（nonterminal） ，代表可以继续扩展或产生的符号，也就是说，当在某条产生式的右边遇到了此非终结符的时候，总是可以用本产生式的右边来替换这个非终结符。
  • 而 “我、你、他、吃、饭、菜” 这些符号是 X 语言中的词，无法再产生新的符号了，称为 终结符（terminal） 。终结符只能出现在产生式的右边，非终结符则左边和右边都可以出现。
  • 上述产生式中有一个特别的非终结符： “语句” ， X 语言中的所有句子都以它为起点产生，这个符号被称为 起始符号（start symbol）。

非终结符和终结符

  • 终结符:通俗的说就是不能单独出现在推导式左边的符号，也就是说终结符不能再进行推导.

详细一点说：终结符是一个形式语言的基本符号。就是说，它们能在一个形式语法的推导规则的输入或输出字符串存在，而且它们不能被分解成更小的单位。确切地说，一个语法的规则不能改变终结符。例如说，下面的语法有两个规则： x -> xa x -> ax 在这种语法之中，a是一个终结符，因为没有规则可以把a变成别的符号。不过，有两个规则可以把x变成别的符号，所以x是非终结符。一个形式语法所推导的形式语言必须完全由终结符构成。

  • 非终结符： 不是终结符的都是非终结符。非终结符可理解为一个可拆分元素，而终结符是不可拆分的最小元素。

非终结符是可以被取代的符号。一个形式文法中必须有一个起始符号；这个起始符号属于非终结符的集合。

  • 判断注意:
    • 只要存在有 S→L ，则 S 必然是个非终结符
    • 逗号，[，]，（，） 这5个都是终结符
    • 一般书上把非终结符用大写字母 表示，而终结符用小写字母表示。