特征预处理

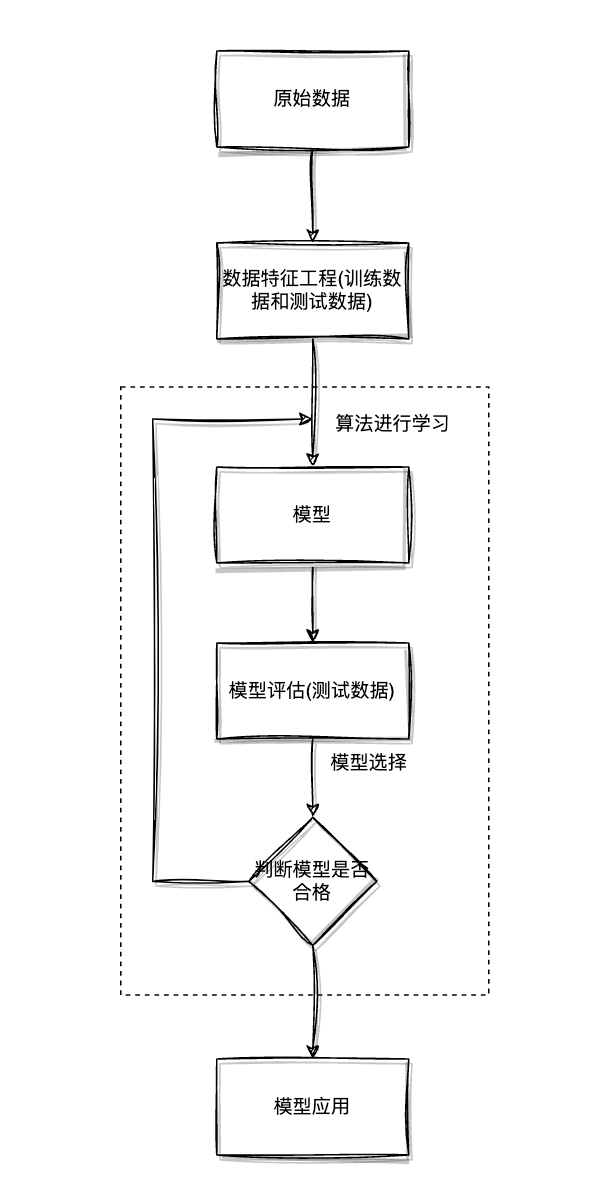
为什么要进行归一化/标准化？

特征的单位或者大小相差较大，或者某特征的方差相比其他的特征要大出几个数量级，容易影响（支配）目标结果，使得一些算法无法学习到其它特征。

特征预处理

作用与某一列，作用与某个特征值内部各各元素。

归一化

$$ X^{\prime}=\frac{x-x_{min}}{x_{max}-x_{min}} $$ 作用于每一列，$x_{max}$为一列的最大值，$x_{min}$为一列的最小值。

$$ \quad X^{\prime \prime}=X^{\prime}*(Range_{a}-Range_{b})+Range_{b} $$

那么X"为最终结果，$Range_{a}$，$Range_{b}$分别为指定区间值默认$Range_{a}=1$, $Range_{b}=0$

注意最大值最小值是变化的，另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。

标准化

平均值(平移)：$$ \bar{x} =\frac{1}{m}\sum_{i=1}^{m}x^{(i)} $$ 标准差(缩放)：$$ \sigma=\sqrt{\frac{\sum_{i=1}^{m}\left(x_{i}-\bar{x}\right)^{2}}{m}} $$

标准差是一组数值自平均值分散开来的程度的一种测量观念。 一个较大的标准差，代表大部分的数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。 例如，两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ，但第二个集合具有较小的标准差。

标准化：$$ X^{\prime}=\frac{x-\bar{x}}{\sigma} $$

使得得到的特征满足均值为0，标准差为1的正态分布，使得原本可能分布相差较大的特征对模型有相同权重的影响。

均值为0：$ \bar{x} =\frac{1}{m}\sum_{i=1}^{m}{X^{\prime}}^{(i)} =\frac{1}{m}\sum_{i=1}^{m}{(\frac{x-\bar{x}}{\sigma})}^{(i)} = \frac{1}{m\sigma}\sum_{i=1}^{m}{(x-\bar{x})}^{(i)} = \frac{1}{m\sigma}(\sum_{i=1}^{m}{(x)}^{(i)}-m\bar{x}) =\frac{1}{\sigma}(\frac{1}{m}\sum_{i=1}^{m}{(x)}^{(i)}-\bar{x}) $

标准差为1： $\sigma=\sqrt{\frac{\sum_{i=1}^{m}\left(X^{\prime}_{i}-\bar{X^{\prime}}\right)^{2}}{m}} $

$ = \sqrt{\frac{\sum_{i=1}^{m}\left(X^{\prime}_{i}\right)^{2}}{m}} $

$ = \sqrt{\frac{\sum_{i=1}^{m}\left(\frac{x-\bar{x}}{\sigma}\right)^{2}}{m}} $

$ = \sqrt{\frac{\sum_{i=1}^{m}\left(x-\bar{x}\right)^{2}}{m}}*\frac{1}{\sigma} = \frac{\sigma}{\sigma} = 1$

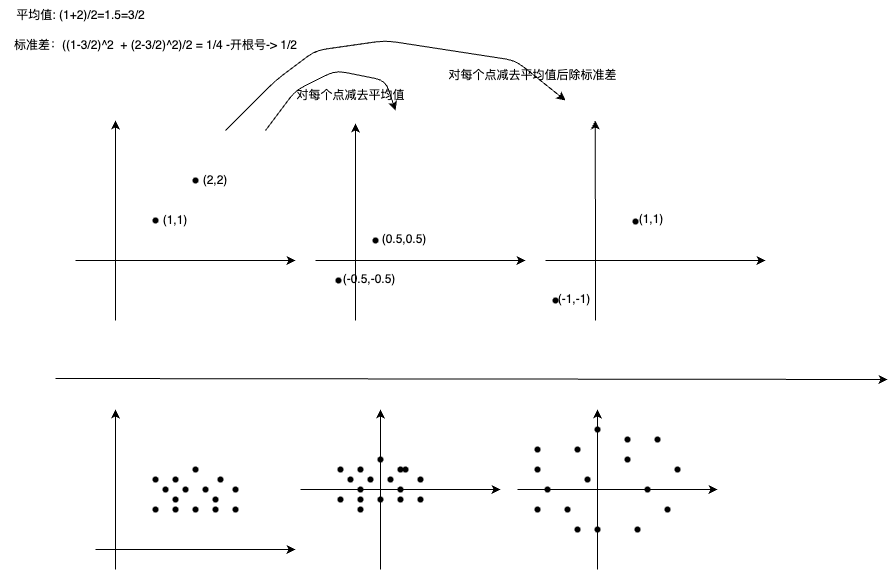
二者比较

具体应该选择归一化还是标准化呢，如果把所有维度的变量一视同仁，

• 在计算距离中发挥相同的作用，应该选择标准化，标准化更适合现代嘈杂大数据场景。
• 如果想保留原始数据中由标准差所反映的潜在权重关系，或数据不符合正态分布时，选择归一化。

总结

对于归一化来说：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变 对于标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小。