降维是指在某些限定条件下，降低随机变量（特征）个数，得到一组“不相关”主变量的过程。

降低随机变量的个数

正是因为在进行训练的时候，我们都是使用特征进行学习。如果特征本身存在问题或者特征之间相关性较强，对于算法学习预测会影响较大。

特征选择

1定义 数据中包含冗余或相关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。

20231118085537

方法

  • Filter(过滤法)：按照发散性或相关性对各个特征进行评分，设定阈值或者待选择特征的个数进行筛选
    • 方差选择法：低方差特征过滤
    • 相关系数：特征与特征之间的相关性
  • Wrapper(包装法)：根据目标函数（往往是预测效果评分），每次选择若干特征，或者排除若干特征
  • Embedded(嵌入法)：先使用某些机器学习的模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征（类似于Filter，只不过系数是通过训练得来的）
    • 决策树：信息熵、信息增益
    • 正则化：L1、L2
    • 深度学习：卷积等

过滤式

基本想法是：分别对每个特征 x_i ，计算 x_i 相对于类别标签 y 的信息量 S(i) ，得到 n 个结果。然后将 n 个 S(i) 按照从大到小排序，输出前 k 个特征。显然，这样复杂度大大降低。那么关键的问题就是使用什么样的方法来度量 S(i) ，我们的目标是选取与 y 关联最密切的一些 特征x_i 。

Pearson相关系数 卡方验证 互信息和最大信息系数 距离相关系数 方差选择法

方差选择法

这种方法先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。

例如，假设我们有一个具有布尔特征的数据集，并且我们要删除超过80％的样本中的一个或零（开或关）的所有特征。布尔特征是伯努利随机变量，这些变量的方差由下式给出:

VarianceThreshold是特征选择的简单基线方法。它删除方差不符合某个阈值的所有特征。默认情况下，它会删除所有零差异特征，即所有样本中具有相同值的特征。代码如下：

  • class原型: sklearn.feature_selection.VarianceThreshold(threshold=0.0)
  • 参数: threshold: 指定方差的阙值，特征的方差低于此阙值将被剔除
  • 成员属性：variances_:一个数组，分别为各特征的方差
  • 成员方法：
    • fit(X,[,y]):从样本数据中学习方差
    • transform(X): 执行特征选择（删除低于阙值的特征）
    • fit_transform(X [,y]) 执行特征选择（删除低于阙值的特征）
    • get_support([indices])
    • True:返回被选出的特征的下标
    • False:返回一个布尔值组成的数组，该数组指示哪些特征被选中

例子： 假设我们有一个bool型的数据集，并且我们想要去掉那些超过80%的样本都取值为0（或者为1）的所有特征。bool型特征是伯努利随机变量，方差为 $\operatorname{Var}(X)=p(1-p)$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

from sklearn.feature_selection import VarianceThreshold
X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
# 方差选择法，返回值为特征选择后的数据
# 参数threshold为方差的阈值
sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
print(sel.fit_transform(X))

输出结果：
array([[0, 1], ​ [1, 0], ​ [0, 0], ​ [1, 1], ​ [1, 0], ​ [1, 1]]) 
# 如预期的那样，VarianceThreshold已经删除了第一列，其具有 p=5/6>0.8 包含零的概率。

方差选择的逻辑并不是很合理，这个是基于各特征分布较为接近的时候，才能以方差的逻辑来衡量信息量。但是如果是离散的或是仅集中在几个数值上，如果分布过于集中，其信息量则较小。而对于连续变量，由于阈值可以连续变化，所以信息量不随方差而变。 实际使用时，可以结合cross-validate进行检验

Pearson相关系数

皮尔森相关系数是一种最简单的，能帮助理解特征和响应变量之间关系的方法，该方法衡量的是变量之间的线性相关性，结果的取值区间为[-1，1]，-1表示完全的负相关，+1表示完全的正相关，0表示没有线性相关。

  • 相关系数的值介于-1与+1之间，即-1≤r≤+1。其性质如下:
    • 当>0时，表示两变量正槽关，r<0时，两变量为负相关。
    • 当|r|=1时，表示两变量为完全相关，当r=0时，表示两变量间无相关关系。
    • 当0<|r|<1时，表示两变量存在一定程度的相关。且越接近1，两变量间线性关系越密切；越接近于0，表示两变量的线性相关越弱。
    • 一般可按三级划分：|r|<0.4为低度相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关。

Pearson Correlation速度快、易于计算，经常在拿到数据(经过清洗和特征提取之后的)之后第一时间就执行。Scipy的 pearsonr 方法能够同时计算 相关系数 和p-value.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

import numpy as np
from scipy.stats import pearsonr
np.random.seed(0)
size = 300
x = np.random.normal(0, 1, size)
y=x+np.random.normal(0, 1, size) #模拟y

# 输入：特征矩阵和目标向量
# 输出： 相关系数值和p值
print("Pearson相关系数:", pearsonr(x, y))

Pearson相关系数的一个明显缺陷是，作为特征排序机制，他只对线性关系敏感。如果关系是非线性的，即便两个变量具有一一对应的关系，Pearson相关性也可能会接近0。例如：

1
2
3

x=np.random.uniform(-1,1,100000)
print pearsonr(x,x**2)[0]
# 结果: -0.00230804707612

主成分分析

主成分分析（Principal Component Analysis，PCA）是一种常用的数据降维技术。其目的是从高维度的数据中提取主要特征，将数据的维度降低到较低的维度，同时尽可能保留大部分原始数据的信息。

  • 定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量
  • 作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
  • 应用：回归分析或者聚类分析当中

具体来说，主成分分析的过程如下：

  1. 对数据进行标准化处理，使得每个变量的均值为0，方差为1。
  2. 计算数据的协方差矩阵。
  3. 对协方差矩阵进行特征值分解，得到特征值和特征向量。
  4. 将特征值按大小排序，选取最大的k个特征值对应的特征向量作为主成分。
  5. 将原始数据映射到选取的主成分上，得到降维后的数据。

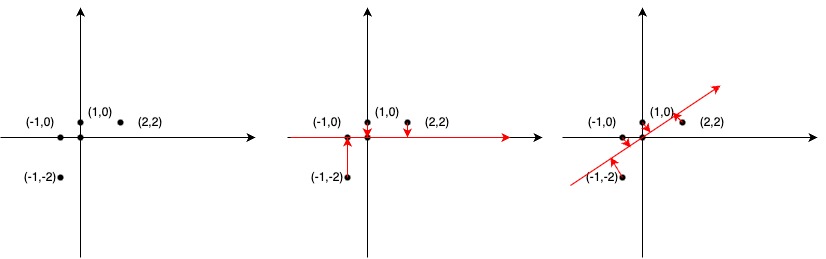
主成分分析的重点在于计算协方差矩阵和特征值分解。协方差矩阵描述了变量间的线性关系，特征值和特征向量是协方差矩阵的数学特性。在数据降维时，我们通过选取最大的k个特征值对应的特征向量作为主成分，保留了数据中的主要变化方向和信息。由于特征值表示了这些主成分解释变量总方差的比例，因此可以根据特征值的大小选择适当的主成分数量，实现数据的降维。

xx

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

from sklearn.decomposition import PCA
def pca_demo():
    """
    PCA降维
    :return:
    """
    data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]

    # 1、实例化一个转换器类
    transfer = PCA(n_components=0.95)

    # 2、调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new)
    return None

if __name__ == "__main__":
    pca_demo()

附录

标准差和方差

差：的意思是离正常有多远。

关于0-1分布的方差推导

0-1分布是一种特殊的离散概率分布，只有两个可能取值：0 和 1。它也被称为伯努利分布或两点分布。

对于一个随机变量 $X$，若 $X$ 服从 0-1 分布，则其方差 $\operatorname{Var}(X)$ 的计算如下：

首先，0-1分布的期望值为 $E(X)=p$，其中 $p$ 是 $X=1$ 的概率，$1-p$ 是 $X=0$ 的概率。

然后，根据方差的定义：

$$ \begin{aligned} \operatorname{Var}(X)&=E[(X-E(X))^2]\ &=E[(X-p)^2] \end{aligned} $$

因为 $X$ 只能取 0 或 1，所以可以将上式展开，得到：

$$ \begin{aligned} \operatorname{Var}(X)&=E[(X-p)^2]\ &=E[X^2-2Xp+p^2]\ &=E(X^2)-2pE(X)+p^2\ &=E(X^2)-2p^2+p^2\ &=E(X^2)-p^2 \end{aligned} $$

最后我们来计算 $E(X^2)$，根据定义：

$$ E(X^2)=\sum_{i=0}^{1} i^2 P(X=i) $$

因为 $X$ 只能取 0 或 1，所以：

$$ E(X^2)=0^2P(X=0)+1^2P(X=1)=0\times(1-p)+1\times p=p $$

带入前面的式子可得：

$$ \operatorname{Var}(X)=E(X^2)-p^2=p-p^2=p(1-p) $$

因此，当 $X$ 服从 0-1 分布时，$\operatorname{Var}(X)=p(1-p)$。

参考

(x mean)/std fit_transform() fit() 计算每一列的平均值、标准差 transform() 带入(X-mean)/std进行最终的转换

20231104181629

3.1 sklearn转换器和估计器 转换器 估计器(estimator) 3.1.1 转换器 - 特征工程的父类 1 实例化 (实例化的是一个转换器类(Transformer)) 2 调用fit_transform(对于文档建立分类词频矩阵，不能同时调用) 标准化： (x - mean) / std fit_transform() fit() 计算 每一列的平均值、标准差 transform() (x - mean) / std进行最终的转换 3.1.2 估计器(sklearn机器学习算法的实现) 估计器(estimator) 1 实例化一个estimator 2 estimator.fit(x_train, y_train) 计算 —— 调用完毕，模型生成 3 模型评估： 1）直接比对真实值和预测值 y_predict = estimator.predict(x_test) y_test == y_predict 2）计算准确率 accuracy = estimator.score(x_test, y_test)