kNN

kNN（k-Nearest Neighbors）算法是一种简单但常用的分类和回归算法。它的核心思想是基于相似性来做预测。具体来说，对于一个测试样本，在训练数据中找到与其距离最近的 k 个训练样本，然后根据这 k 个样本的标签进行预测。

原理

对于给定的一个测试样本x，kNN 算法的分类过程如下：

  • 计算测试样本 x 与每个训练样本之间的距离；
  • 选取距离最近的 k 个训练样本；
  • 根据这 k 个样本的标签，通过投票的方式确定测试样本的类别。

对于回归问题而言，kNN 算法的过程也是类似的，只不过最后的预测结果是这k个样本的平均值。

在实现时，我们需要选择一个合适的距离度量方法和一个合适的 k 值。 通常，欧式距离是最常用的距离度量方法。而 k 的取值则需要通过交叉验证等方法来确定。

举例

假设我们有如下的数据集，其中每个样本包含两个特征 $x_1$ 和 $x_2$，以及它们对应的类别标签：

x1x2标签
11A
22A
21A
53B
62B
64B

现在我们要对以下测试样本进行分类：

$x_1$$x_2$
32

我们使用 kNN 算法进行分类，假设 k=3。首先计算测试样本与训练集中每个样本之间的距离：

距离标签
$\sqrt{(3-1)^2+(2-1)^2}=\sqrt{5}$A
$\sqrt{(3-2)^2+(2-2)^2}=1$A
$\sqrt{(3-2)^2+(2-1)^2=\sqrt{2}}$A
$\sqrt{(3-5)^2+(2-3)^2}=\sqrt{3}$B
$\sqrt{(3-6)^2+(2-2)^2}=3$B
$\sqrt{(3-6)^2+(2-4)^2}=\sqrt{13}$B

可以发现，距离最近的三个样本分别是 $(2,2)$、$(2,1)$ 和 $(5,3)$，它们的类别分别是 A、A 和 B。因此，这三个样本的投票结果是 A，所以测试样本 $(3,2)$ 被归类为 A 类。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

def knn_iris():
    """
    用KNN算法对鸢尾花进行分类
    :return:
    """
    # 1）获取数据
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3）特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）KNN算法预估器
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)
    # 5）模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    return None

if __name__ == "__main__":
    # 代码1： 用KNN算法对鸢尾花进行分类
    knn_iris()

距离

欧式距离

欧氏距离是最容易直观理解的距离度量方法, 我们小学、初中和高中接触到的两个点在空间中的距离一般都量指欧氏距离。

一维平面上点 $a(x_{1}, y_{1})$ 与 $b(x_{2}, y_{2})$ 间的欧氏距离: $$ d_{12}=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}} $$

三维空间点 $a(x_{1}, y_{1}, z_{1})$ 与 $b(x_{2}, y_{2}, z_{2})$ 间的欧氏距离: $$ d_{12}=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{1}-z_{2}\right)^{2}} $$

n维空间点 $a(x_{11}, x_{12}, \ldots, x_{11})$ 与 $b(x_{21}, x_{22}, \ldots, x_{2n})$ 间的欧氏距离 (两个n维向量): $$ d_{12}=\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-x_{2 k}\right)^{2}} $$

曼哈顿距离

一维平面两点 $(x_{1}, y_{1})$ 与 $b\left(x_{2},x_{2}\right)$ 间的曼哈顿员离: $$\quad d_{12}=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|$$

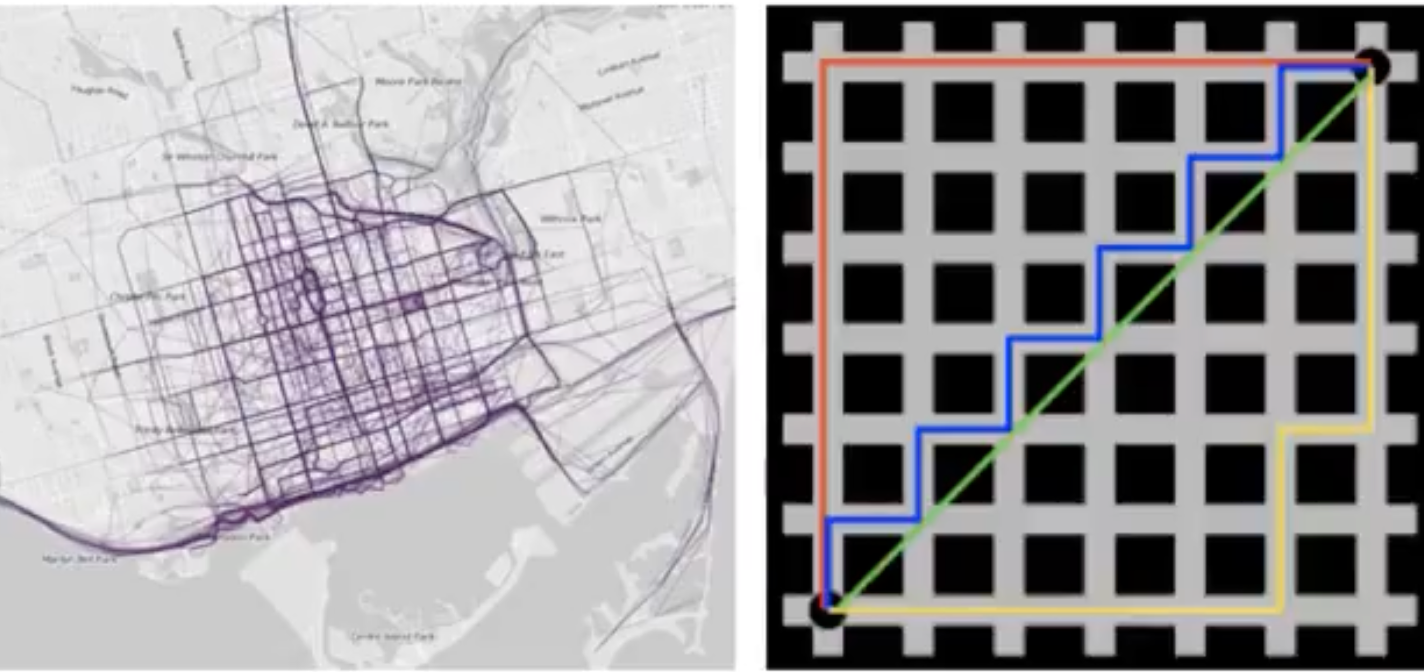
20231125141133

n维空间点 $a\left(x_{11}, x_{12}, \ldots, x_{11}\right)$ 与 $b\left(x_{21}, x_{22}, \ldots, x_{2 n}\right)$ 的曼哈顿距离：$$ d_{12}=\sum_{k=1}^{n}\left|x_{1 k}-x_{2 k}\right| $$

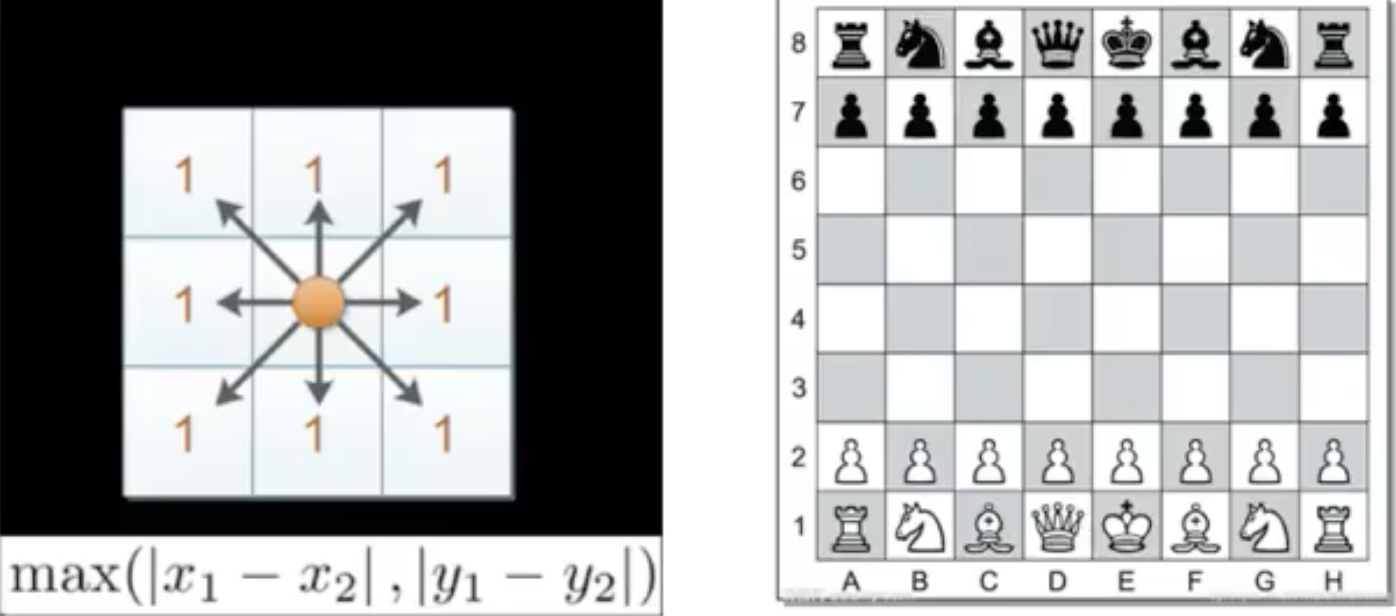
切比雪夫距离(Chebyshev Distance)

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。

一维平面两点 $a\left(x_{1}, y_{1}\right)$ 与 $b\left(x_{2}, y_{2}\right)$ 间的切比雪夫距离: $$ d_{12}=\max \left(\left|x_{1}-x_{2}\right|,\left|y_{1}-y_{2}\right|\right) $$

n 维空间点 $a\left(x_{11}, x_{12}, \ldots, x_{1n}\right)$ 与 $b\left(x_{2}, x_{22}, \ldots, x_{21}\right)$ 的切比雪夫距离: $$ d_{12}=\max \left(\left|x_{1 i}-x_{2 i}\right|\right) $$

20231125141609

闵可夫斯基距离(Minkowski Distance)

闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。两个n维变量a(x11,x12,,x1n)与b(x21,x22,..,x2n)间的闵可夫斯基距离定义为：

$$ d_{12}=\sqrt[p]{\sum_{k=1}^{n}\left|x_{1 k}-x_{2 k}\right|^{p}} $$

  • 其中p是一个变参数:
    • 当p=1时, 就是曼哈顿距离;
    • 当p=2时, 就是欧氏距离;
    • 当 $p \rightarrow \infty$ 时, 就是切比雪夫距离。 根据p的不同, 闵氏距离可以表示某一类/种的距离。

优缺点

  • kNN 算法的优点包括：

    • 简单、易于理解和实现；
    • 对于多分类问题效果很好；
    • 适用于大规模数据集，需要的存储空间少。

  • kNN 算法的缺点包括：

    • 需要事先确定k的取值；
    • 对于高维数据或者特征空间非常稀疏的数据，效果较差；
    • 需要计算测试样本与所有训练样本之间的距离，计算量较大；
    • 对于不平衡数据集的处理较为困难。

超参数

什么是超参数？

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

交叉验证

在机器学习任务中，为了得到最优模型, 我们需要将数据集划分成训练集，验证集和测试集。 测试集不参与训练模型,只用于评估最终模型的精度，训练模型的任务由训练集来完成，验证集会帮助我们调节超参数，从而找到一组最优的超参数组合，这里的最优是指的模型在验证集上的最好评估效果。

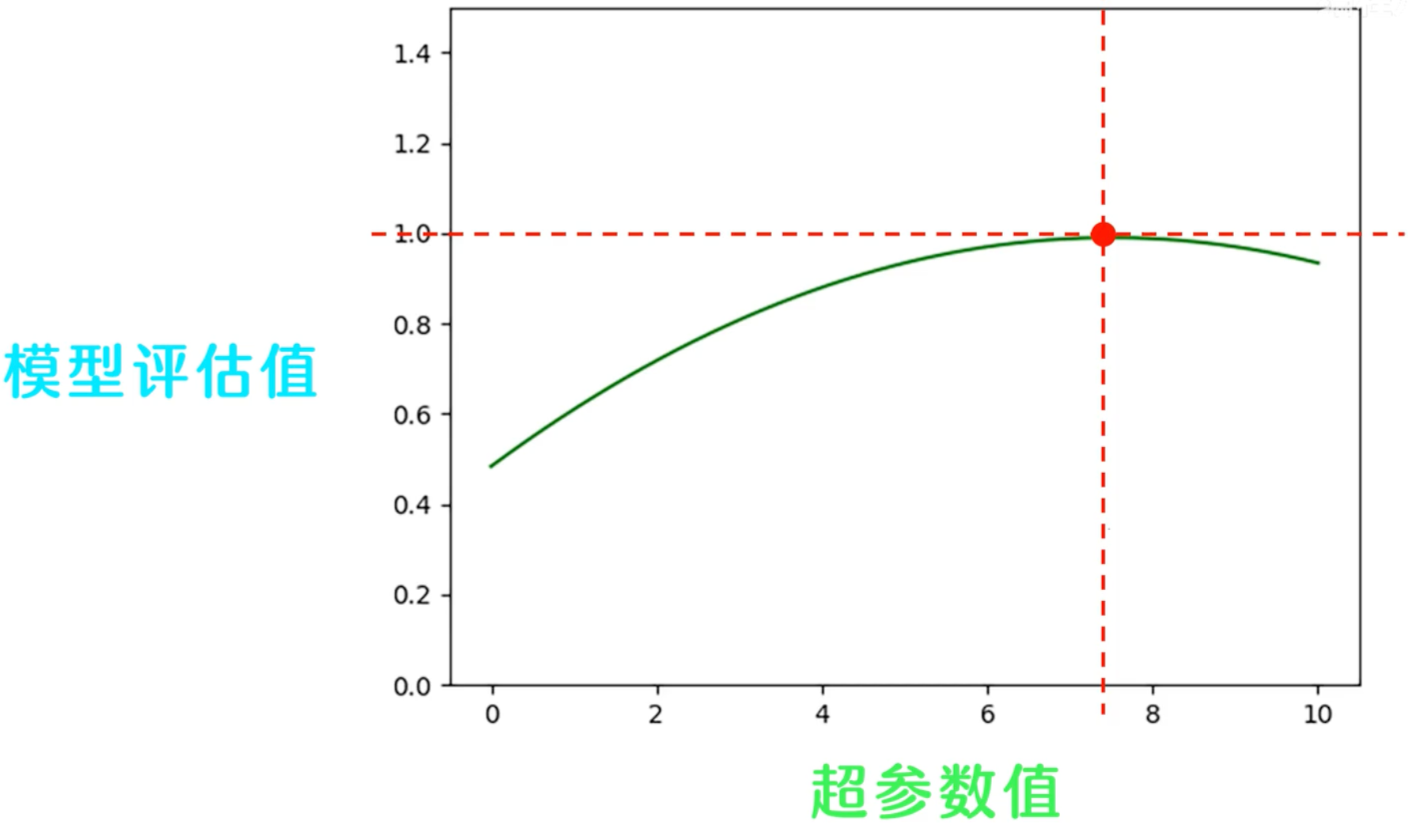
调节超参数的过程如下：我们将超参数值作为横坐标，模型评估值作为纵坐标，不同的超参数训练出的模型，在验证集上会产生不同的评估结果。 模型评估值随着超参数值的变化而变化，进而会得到一条曲线： 20231123222756

曲线上评估值最高的点对应的超参数值，就是我们要找的最优超参数，当数据集数量较多的时候，我们可以用上述调参流程来确定超参数。 但当数据集的数量不够充足时，比如数量不足1万时，这种方法就会导致验证集的数量过少，使得验证集无法完全覆盖所有训练样本的特征分布。

举个极端一点的例子，比如在某个人脸检测任务中，只有三个样本，一个是亚洲人的脸，一个是欧洲人的脸，一个是非洲人的脸，她们的特征差异都非常大，如果只拿其中一种人脸做验证集，显然很难评估出模型在其他人脸上的表现能力，也就是说，如果验证集的数量数据太少，不能完全表示训练集的特征分布，那验证集评估出来的模型效果也是不可靠的。

这个时候我们选一部分数据做验证集，得到评估曲线

1

训练集_训练集_验证集|测试集

之后换成另一部分做验证集, 得到另一条评估曲线。之前表现最优的超参数现在又不是了。那面对这样的情况，我们该如何解决呢？

1

验证集_训练集_训练集|测试集

一般使用交叉验证(cross-Validation)的方法来确定最优的超参数组合。 交叉是指训练集和验证集之间的数据相互转换，让测试集依旧保持不动。

将训练集分成K份，每次取其中一份做验证集，剩下的K-1份还是训练集，之后再取第二份做验证集，剩下的K-1份也还是训练集。这样经过K次之后所有的数据就都参与了训练，也都参与了验证，得到了K条参数-评估值曲线。

把这些曲线取均值，就会得到一条均值曲线，评估值最高的点对应的超参数值，就是我们要找的最优超参数。

1
2
3
4
5

训练集_训练集_..._训练集_|测试集
        K份

[验证集]_训练集_..._训练集_|测试集
训练集_[验证集]_..._训练集_|测试集
  • 这种将训练集拆分成K份的方法又称为K折交叉验证。
  • 在数据极度缺乏的情况下，我们每次只取一个样本做验证集，此时的K和数据的个数相等。这种验证方式叫做留一交叉验证,主要用于数据极少的情况下。
  • sklearn.model_selection.GridSearchCV(estimator,param_grid=None,cv=None): 对估计器的指定参数值进行详尽搜索
    • estimator:估计器对象
    • param_grid:估计器参数(dict)M“n_neighbors":[1,3,5]}
    • cv:指定几折交叉验证
  • fit():输入训练数据
  • score():准确率
  • 结果分析：
    • 最佳参数：best_params_
    • 最佳结果：best_score_
    • 最佳估计器：best_estimator_
    • 交叉验证结果：cv_results_
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.tree import DecisionTreeClassifier, export_graphviz

def knn_iris_gscv():
    """
    用KNN算法对鸢尾花进行分类，添加网格搜索和交叉验证
    :return:
    """
    # 1）获取数据
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3）特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）KNN算法预估器
    estimator = KNeighborsClassifier()

    # 加入网格搜索与交叉验证
    # 参数准备
    param_dict = {"n_neighbors": [1, 3, 5, 7, 9, 11]}
    estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)
    estimator.fit(x_train, y_train)

    # 5）模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    # 最佳参数：best_params_
    print("最佳参数：\n", estimator.best_params_)
    # 最佳结果：best_score_
    print("最佳结果：\n", estimator.best_score_)
    # 最佳估计器：best_estimator_
    print("最佳估计器:\n", estimator.best_estimator_)
    # 交叉验证结果：cv_results_
    print("交叉验证结果:\n", estimator.cv_results_)

    return None

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183

y_predict:
 [0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
 0]
直接比对真实值和预测值:
 [ True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True False  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True]
准确率为：
 0.9736842105263158
最佳参数：
 {'n_neighbors': 3}
最佳结果：
 0.9553030303030303
最佳估计器:
 KNeighborsClassifier(n_neighbors=3)
交叉验证结果:
 {
    "mean_fit_time": [
        0.00033779144287109374,
        0.00017638206481933593,
        0.00017495155334472655,
        0.00017383098602294922,
        0.00017740726470947266,
        0.00017175674438476562
    ],
    "std_fit_time": [
        0.00039807055683951107,
        3.656131614057078e-06,
        2.388473469995154e-06,
        4.909860029031385e-06,
        1.150277608441172e-05,
        2.1115865540966536e-06
    ],
    "mean_score_time": [
        0.000801992416381836,
        0.0006023883819580078,
        0.000600886344909668,
        0.0005937337875366211,
        0.0006319761276245117,
        0.0005918264389038086
    ],
    "std_score_time": [
        0.0004498697772650859,
        1.9847598505666974e-05,
        2.815662854970172e-05,
        1.3391422114781752e-05,
        6.705592367020572e-05,
        1.2143465964991082e-05
    ],
    "param_n_neighbors": [
        1,
        3,
        5,
        7,
        9,
        11
    ],
    "params": [
        {
            "n_neighbors": 1
        },
        {
            "n_neighbors": 3
        },
        {
            "n_neighbors": 5
        },
        {
            "n_neighbors": 7
        },
        {
            "n_neighbors": 9
        },
        {
            "n_neighbors": 11
        }
    ],
    "split0_test_score": [
        0.9166666666666666,
        0.9166666666666666,
        1.0,
        1.0,
        0.9166666666666666,
        0.9166666666666666
    ],
    "split1_test_score": [
        1.0,
        1.0,
        1.0,
        1.0,
        1.0,
        1.0
    ],
    "split2_test_score": [
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091
    ],
    "split3_test_score": [
        0.9090909090909091,
        1.0,
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        1.0
    ],
    "split4_test_score": [
        1.0,
        1.0,
        1.0,
        1.0,
        1.0,
        1.0
    ],
    "split5_test_score": [
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091
    ],
    "split6_test_score": [
        0.9090909090909091,
        0.9090909090909091,
        0.9090909090909091,
        1.0,
        1.0,
        1.0
    ],
    "split7_test_score": [
        0.9090909090909091,
        0.9090909090909091,
        0.8181818181818182,
        0.8181818181818182,
        0.8181818181818182,
        0.8181818181818182
    ],
    "split8_test_score": [
        1.0,
        1.0,
        1.0,
        1.0,
        1.0,
        1.0
    ],
    "split9_test_score": [
        1.0,
        1.0,
        1.0,
        1.0,
        1.0,
        1.0
    ],
    "mean_test_score": [
        0.9462121212121211,
        0.9553030303030303,
        0.9454545454545455,
        0.9545454545454547,
        0.9462121212121211,
        0.9553030303030303
    ],
    "std_test_score": [
        0.043972035942216534,
        0.04474830128976474,
        0.06030226891555273,
        0.06098367211363062,
        0.05988683083021718,
        0.060459102129481135
    ],
    "rank_test_score": [
        4,
        1,
        6,
        3,
        4,
        1
    ]
}