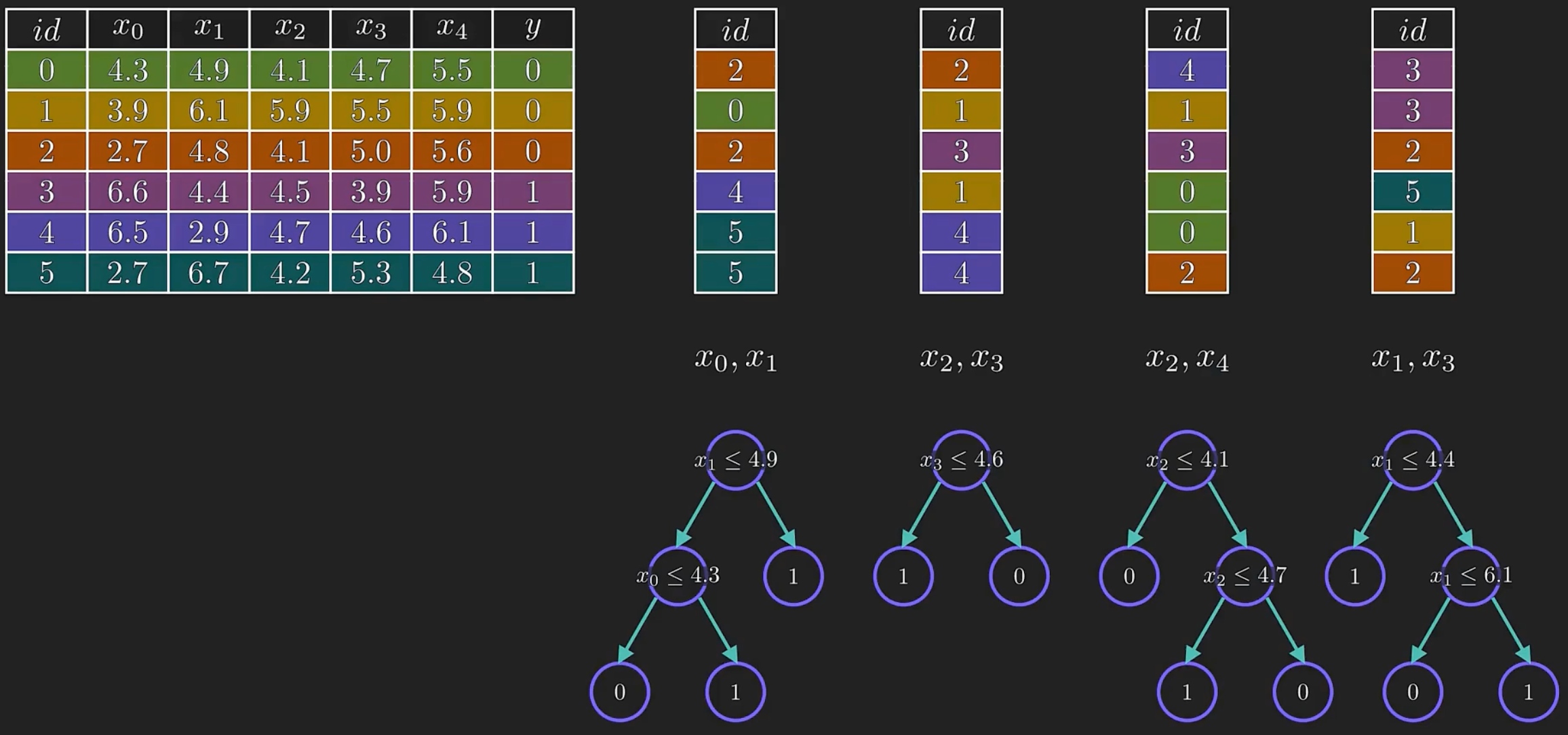
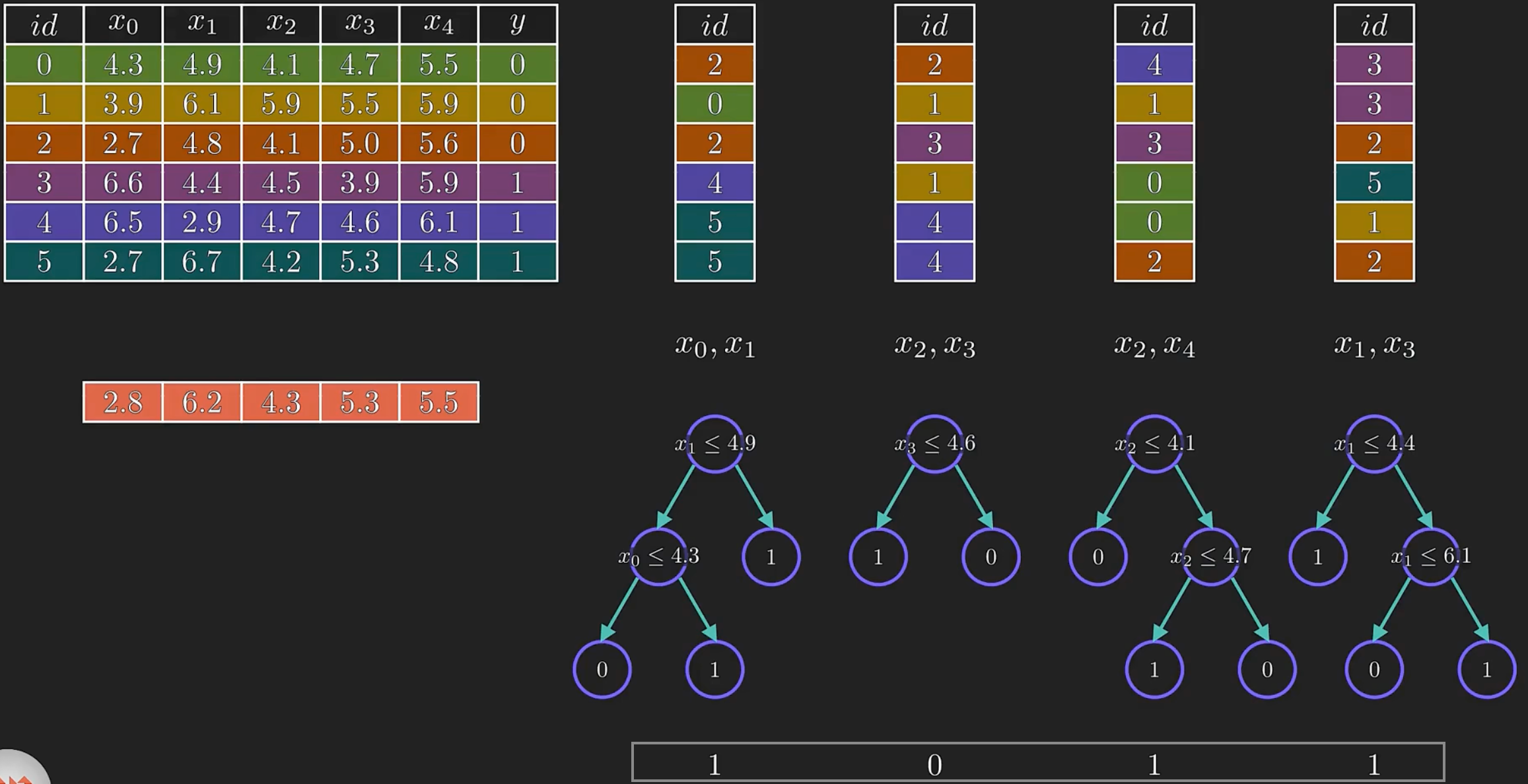
决策树是一种基于树结构的机器学习算法,通常用于分类和回归分析。它通过一系列的问题或判断来建立一个树状模型,每个节点代表一个判断或决策,每个叶子节点代表一个分类结果或输出结果。
举例
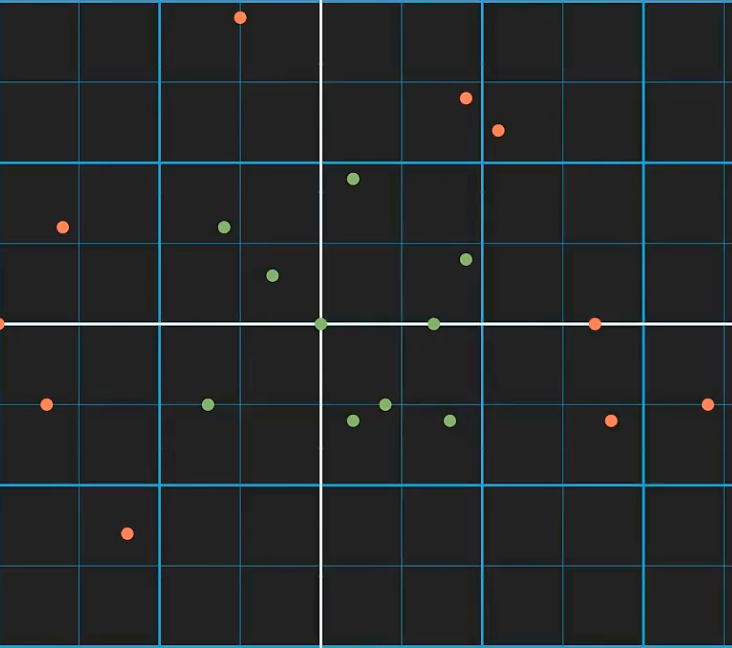
你不能仅仅画一条线把上图红绿点分开,
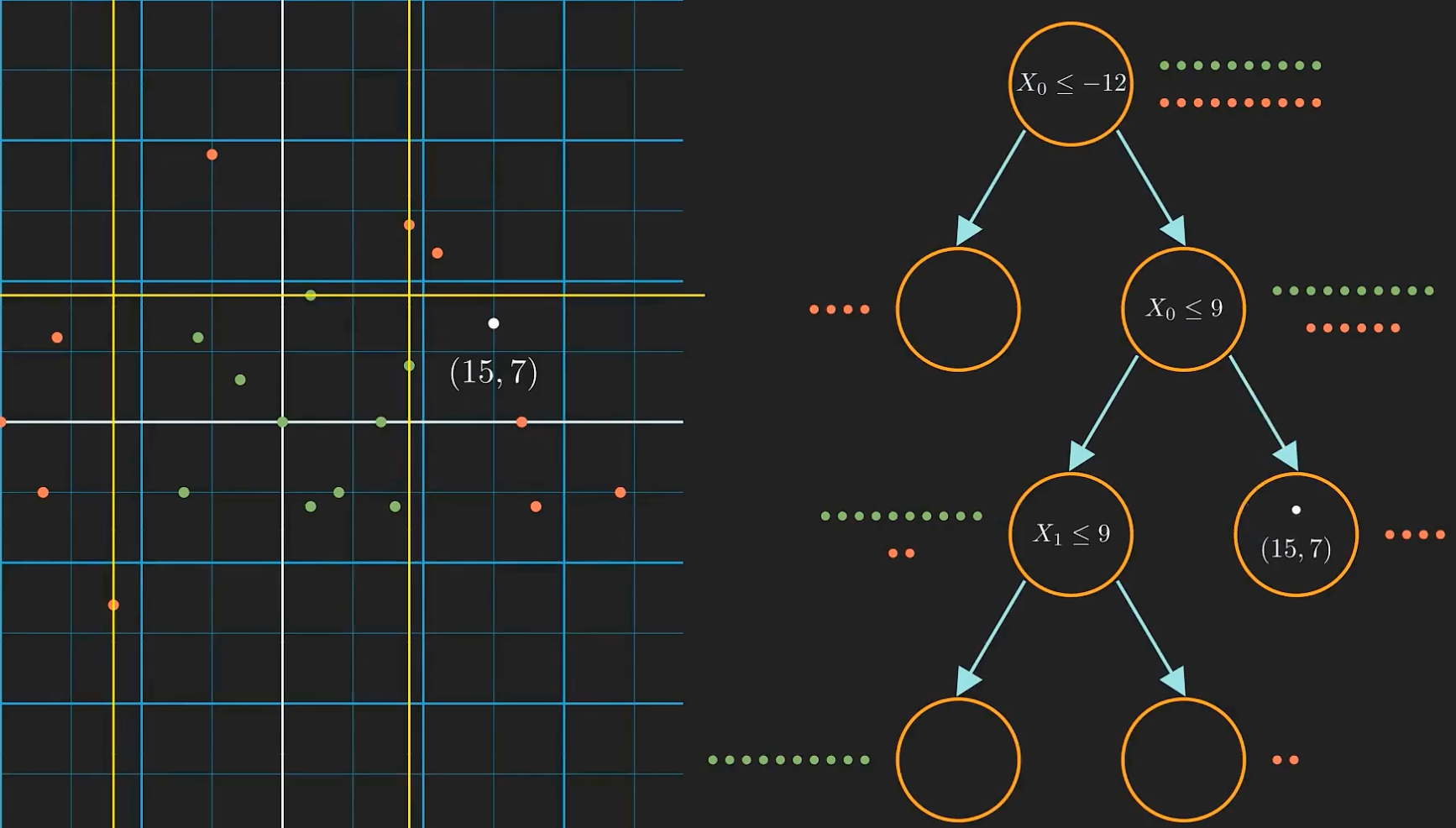
这就是使用二叉决策树进行分类的方法,但这只是一大堆嵌套的if-else语句,如何把它当做是机器学习呢?
主要是如何知道正确的条件呢?因为太多可能得分割条件了。
我们的模型需要学习哪些特征和相应的正确阈值才能最好地分割数据,而这就是它被称为机器学习的原因。
如何决定最佳的分割?
信息增益
先从根节点开始看起,我们手头上有所有的数据,然后我们会比较两种不同的分割方法,
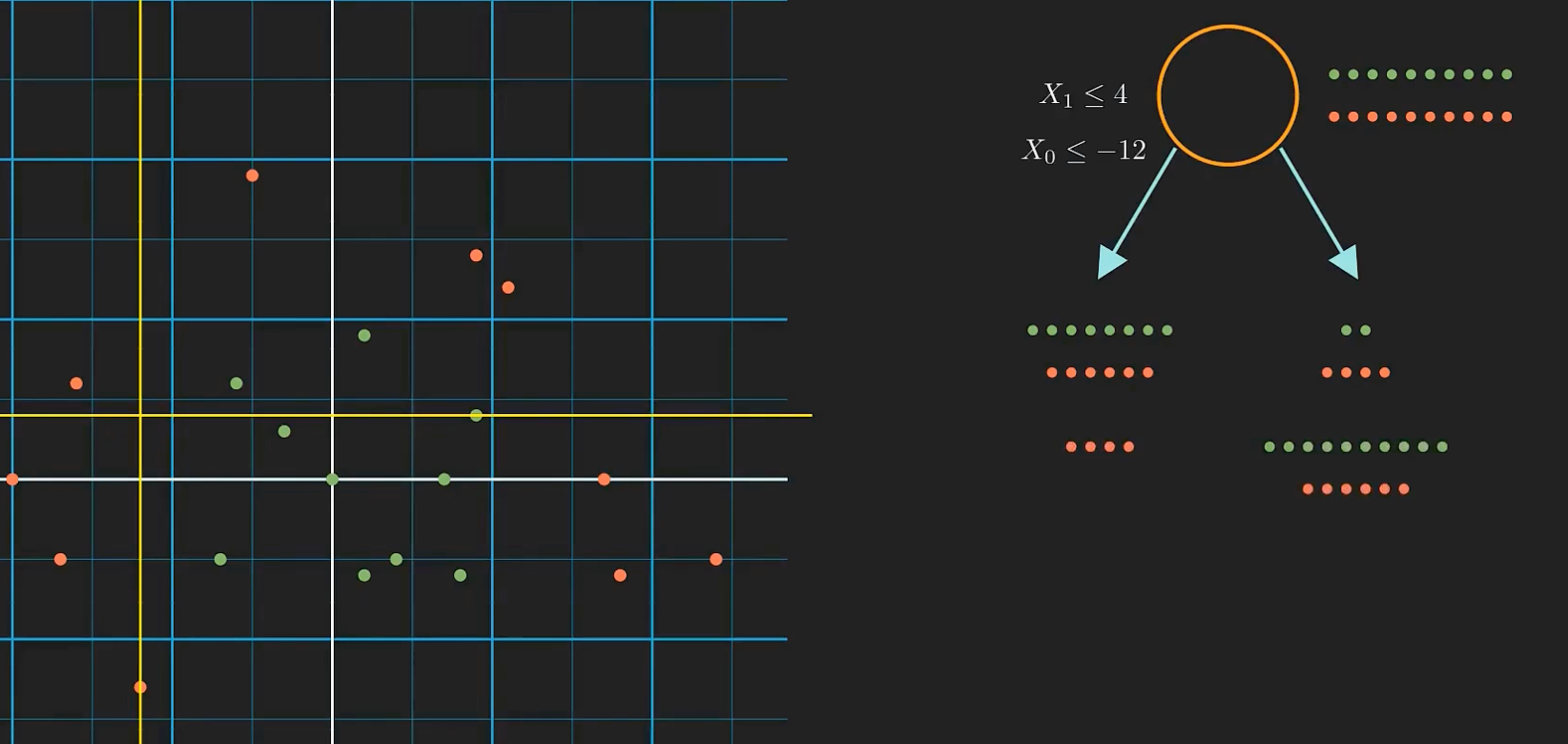
模型会选择那种能最大化信息增益的分割方式。要计算信息增益,需要了解一个状态所包含的信息量。
在根状态,红点与旅店的数量是一样的,假设我们现在要预测一个随机选出的点的类别,只有一般的几率我们能够预测正确,这意味着这个状态的不纯度或者不确定性是最大的。
我们用熵来表示这种情况。熵是一个状态所包含的信息量的度量。
当熵很高时,我们很难确定一个随机算出的点是什么,因此需要跟多的位数来描述这个状态。
$$
Entropy(熵)=\sum-p_{i} \log \left(p_{i}\right)
$$
$p_i$表示第i类的概率
- 所以我们分别来计算一下上图的熵:
- 根节点: $ -0.5log(0.5)-0.5log(0.5)=1$
- 左上角: $-0.57log(0.57)-0.43log(0.43)=0.99$
- 右上角: $-0.33log(0.33)-0.67log(0.67)=0.91$
- 左下角: $-1log(1)-0log(0)=0$
- 右下角: $-0.63log(0.63)-0.37log(0.37)=0.95$
所以左下角的熵是最小的。
要找到对应于某个分割的信息增益,需要从父节点的熵中减去子节点的总熵。
$$
\mathrm{IG}=E(\text { parent })-\sum w_{i} E\left(\text { child }_{i}\right)
$$
$w_i$是权重,表示子节点相对于父节点的大小。
到此,信息增益就可以计算了:
- $ IG_1 = 1-\frac{14}{20}*0.99-\frac{6}{20}*0.91 = 0.034 $
- $ IG_2 = 1-\frac{4}{20}*0-\frac{16}{20}*0.95 = 0.24 $
第二种分割方式给出了更大的信息增益,所以我们才选择它。
模型会比较每一种可能得分割方式,并选择那种能最大化信息增益的方式。模型会遍历每一个可能得特征和特征值,寻找最好的特征以及对应的阈值。
决策树是一种贪心算法,他会选择当前最佳的分割,也就是最大化信息增益的分割。当不会改变之前的分割,后续的分割都依赖于之前的分割。
举例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz
def decision_iris():
"""
用决策树对鸢尾花进行分类
:return:
"""
# 1)获取数据集
iris = load_iris()
# 2)划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
# 3)决策树预估器
estimator = DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train, y_train)
# 4)模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法2:计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
# 可视化决策树
export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
return None
if __name__ == "__main__":
# 用决策树对鸢尾花进行分类
decision_iris()
|
1
2
3
4
5
6
7
8
9
10
| y_predict:
[0 2 1 2 1 1 1 1 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 1 2 2 1 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True False True True True True
True True True True True True False True True True True True
True True False True True False True True True True True True
True True]
准确率为:
0.8947368421052632
|
随机森林
随机森林是一种集成学习算法,它将多个决策树模型组合起来进行预测。随机森林中的每个决策树都是通过对训练数据集的随机采样和特征选择生成的,并且每个决策树只考虑了部分特征。这种随机性可以减少过拟合现象,提高模型泛化性能。
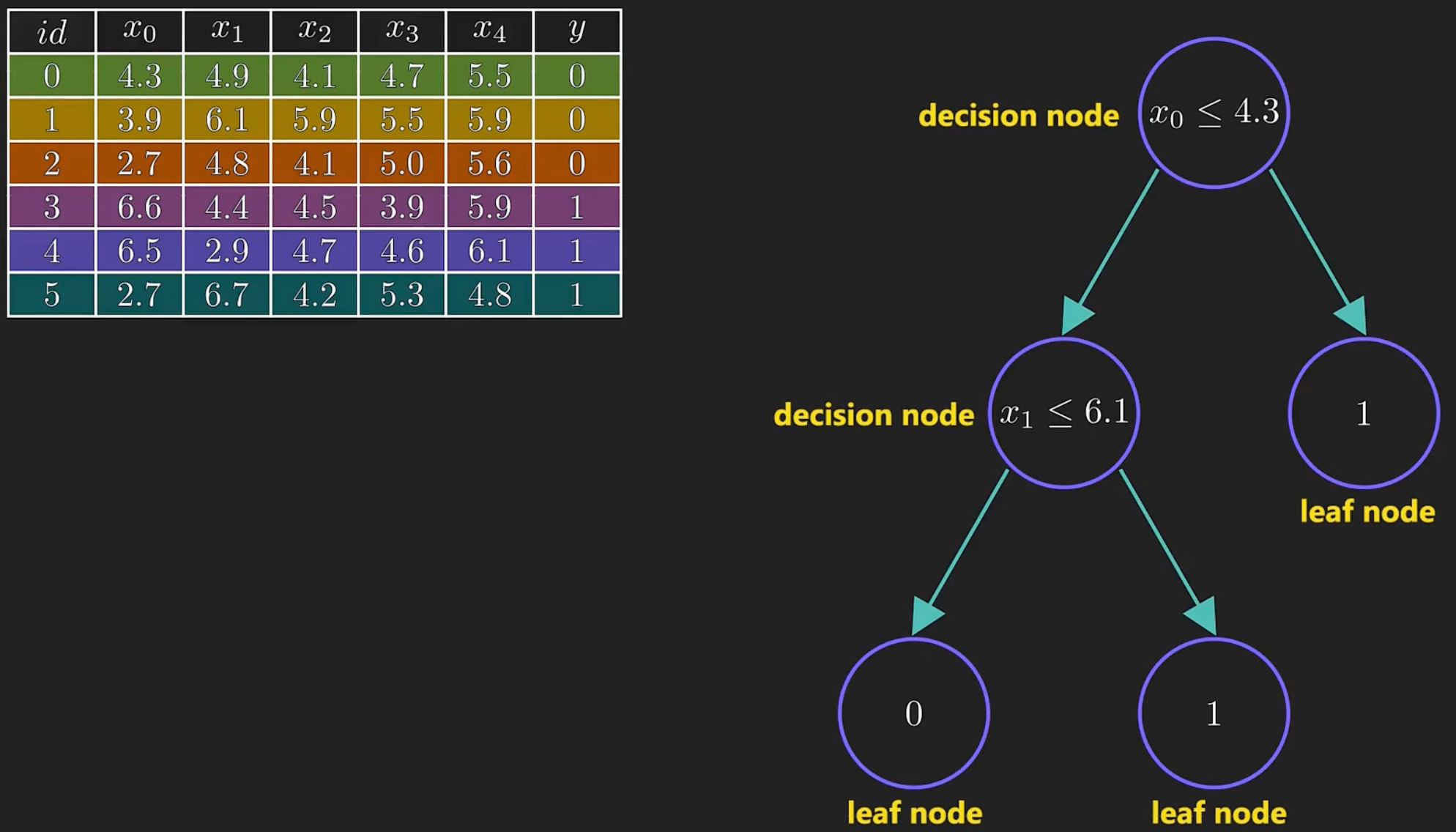
当调整记录一的两个特征,它的决策树变化非常大:
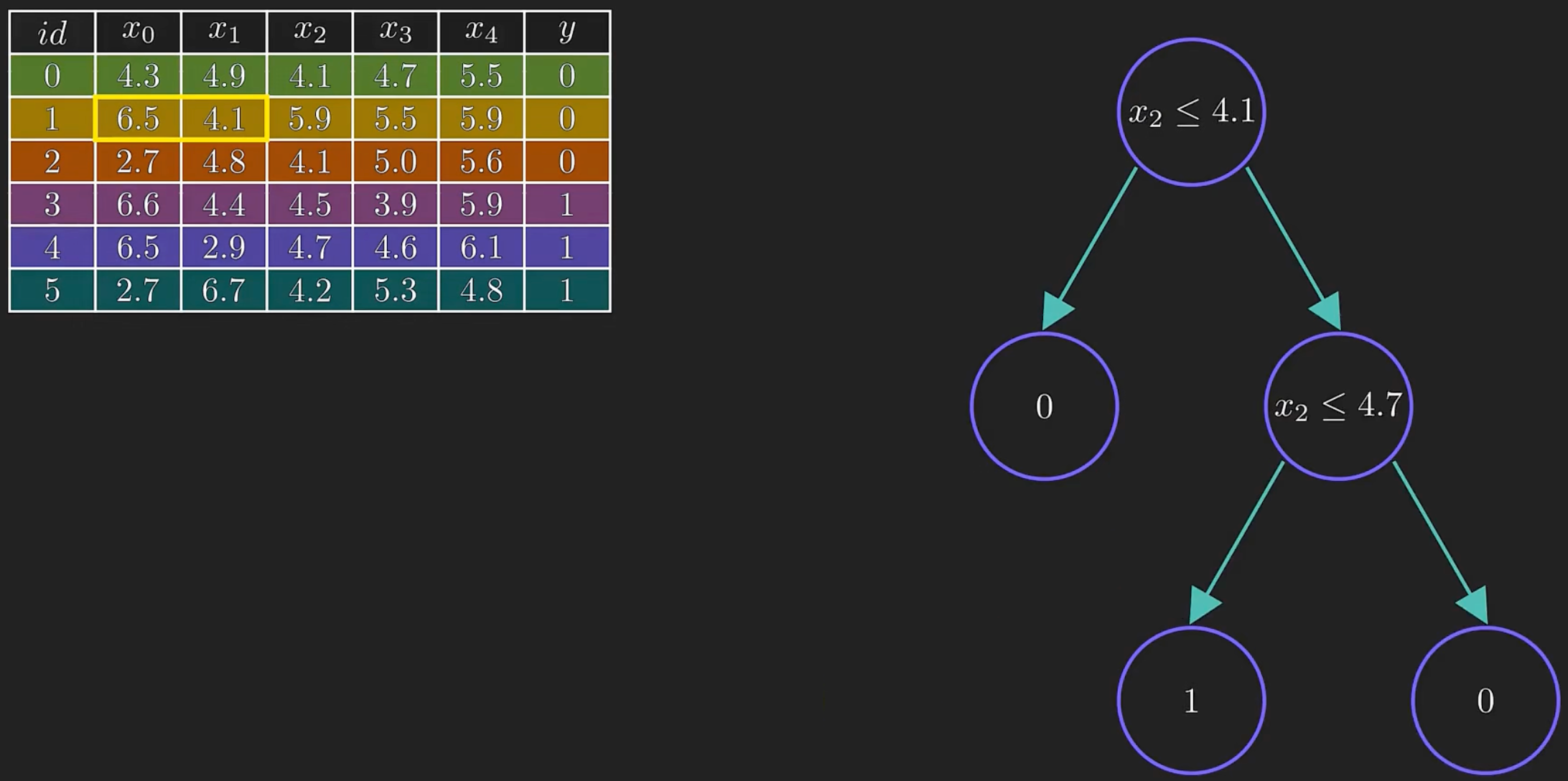
这就说明决策树对训练数据非常敏感,容易产生高分差,这样的模型在泛化上面就会有问题。
随机森林其实就是一群随机生成的决策树,对训练数据的敏感度要小的多。想象一下我们用了好多棵树,所以叫它森林。
- 随机森林的生成过程:
从原始数据集中随机选择 n 个样本作为新的训练数据集(有放回的随机:抽出样本后重新放回)。
从所有特征中随机选择 k 个特征,用于生成决策树。
根据所选的特征和样本,使用基尼系数或信息增益等指标生成决策树模型。
重复步骤 1~3,生成多个不同的决策树模型。
- 对于分类问题,随机森林使用投票的方式进行预测。(在森林中每棵树进行预测,聚合结果)
- 对于回归问题,随机森林使用平均值的方式进行预测。
随机:自举和随机选择特征。自举能确保我们每棵树使用的数据不同,能降低模型对原始训练数据的敏感度。随机选择特征有助降低树与树之间的关联性,如果使用所有的特征,那么大多数的决策节点都会相同,这样他们的行为会非常相同,会增加方差。
特征子集的大小一般取总特征数的对数或平方根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
def suijisanli_demo():
# 1、获取数据
path = "http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt"
titanic = pd.read_csv(path)
# 筛选特征值和目标值
x = titanic[["pclass", "age", "sex"]]
y = titanic["survived"]
# 2、数据处理
# 1)缺失值处理
x["age"].fillna(x["age"].mean(), inplace=True)
# 2) 转换成字典
x = x.to_dict(orient="records")
# 3、数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 4、字典特征抽取
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
#随机森林预估器
estimator = RandomForestClassifier()
# 加入网格搜索与交叉验证
# 参数准备
param_dict = {"n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
estimator.fit(x_train, y_train)
# 5)模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法2:计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
# 最佳参数:best_params_
print("最佳参数:\n", estimator.best_params_)
# 最佳结果:best_score_
print("最佳结果:\n", estimator.best_score_)
# 最佳估计器:best_estimator_
print("最佳估计器:\n", estimator.best_estimator_)
# 交叉验证结果:cv_results_
print("交叉验证结果:\n", estimator.cv_results_)
if __name__ == '__main__':
suijisanli_demo()
|